Vocabulary
Exponential Functions
Monomials
Exponent Rules
Exponential
Functions - 2
Functions - 2
100
What does a represent in y=abx
Initial Value
100
What is the formula for exponential growth?
y = a(1+r)x
100
Subtract -4ab2 from -10ab2
-6ab2
100
Write out the product rule
xa*xb = xa+b
100
Determine if the function shows exponential growth or decay?
y=3(.67)x
Exponential decay
200
The set of all possible output values (y-values) is what?
The Range
200
Which one is an exponential function
Function A)
x:0,1,2 ,3
y:2,4,6,8
Function B)
x:0,1,2,3
y:3,9,27,81
Function B
200
(1/4)(8mn)(-6m2n2)
-12m3n3
200
Write out the quotient rule
xa/xb = xa-b
200
f(x)=a(1.07)x
Does this functions represent exponential growth or decay? What's the percent growth/decay factor?
Exponential Growth. 7%.
300
What is the numerical factor of a term containing a variable (e.g., 3 in 3x)
Coefficient
300
Write the exponential function using the real world problem below.
Sophia buys a motorcycle for 600 dollars and the price depreciates by 50% after one year.
600(.5) = 300
300
(3x)2 * (1/2)-3
72x2
300
Write out the Power Rule
(xa)b= xa*b
300
Does the graph represent exponential growth or decay?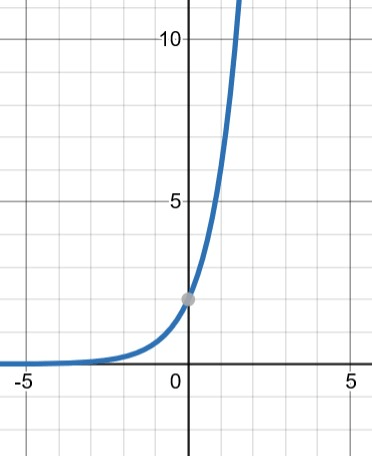 
Exponential Growth
400
What does zeros mean?
The x- values where f(x) = 0
(Aka the roots)
400
Is this exponential growth or decay?
What is the percent growth/decay rate?
y=12(0.7)x
Decay. 30%
400
Simplify. Answer must contain positive exponents only.
-9x8y3 ⋅ 4x-2y11 + 7x6y14
-29 x6 y14
400
Write out the Zero Exponent Rule
x0=1
400
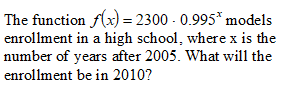
2243
500
This is an invisible line that the graph approaches, but never touches or crosses. It affects exponential graphs.
Asymptote
500
Annual sales of a fast food restaurant are $450,958.87 and increasing at a rate of 7%. What will the annual sales be in 6 years?
450,874(1.07)6 =$676,767.66
500
2 x4y3z5 - ¼ * x2yz5 * (xy)2
1¾ x4y3z5
500
Write out the Negative Exponent Rule
x-a= 1/xa
500
Ms. Wiggins purchased a car for 26,400 and every year it decays by 12%. What can she expect the value of her car to be after 3.5 years?
f(x)=26400(.88)3.5=$16,876.92