5.1
5.2
5.3
5.5
5.6
100
What are the three steps to finding a Perpendicular Bisector.
Step 1: Find the Side at the bottom of the triangle
Step 2: Find the middle
Step 3: At the middle draw in the perpendicular.
100
How is a Median Different for a Perpendicular bisector.
A Median only connects top the opposite side of the triangles midpoint and connects to the vertex. A perpendicular bisector makes a right angle and doesn't start at the vertex.
100
Why do we apply inequalities to triangles & what is the four most common ones we use.
We apply inequalities so we can find which measure are greater than other and less than others.
100
What is this theorem- The sum of the lengths of any two sides must be greater than the remaining sides.
Triangle Inequalities Theorem
100
What is this theorem: If two side of triangle are congruent of 2 side of another triangle and the included angle is larger in the first triangle , then the 3rd side in first triangle will be larger in the second triangle.
The Hinge Theorem
200
Which Point is the Circumcenter of the Perpendicular Bisector.
Point O
200
Medians & Altitudes have different names for their points of concurrency, and what is the definition of both.
Median has a centroid which is the center point when all three medians meet.
Altitudes have a orthocenter which is the point where all three altitudes meet.
200
This theorem states that the longest side of a triangle is directly opposite the large angle.
This is called the Angle Side Relationship
200
Solve is this a triangle - 3,4,5
3+4>5
4+5>3
3+5>4
Yes
200
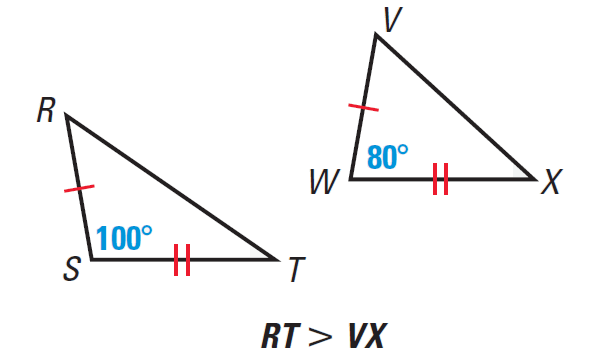
Solve using hinge theorem.
RS=VW
ST=WX
<S > <W
100 > 80
Therefore RT > VX
300
A angle bisector cuts an angle in half what is the two steps to achieving this.
Step 1: Cut the Angle in half
Step 2: Construct Line
EX. Do for all three to find Incenter
300
Using the Centroid theorem solve if QP=12 than SV=3 and SR=6 than what is QU
QU= 9 because of using the centroid 2/3 than you would get 6 add that to 3 you get 9.
300
Solve if you had a triangle called ABC and the angle measures are <A=80 , <B=60 and <C=40. What is the longest side.
The longest side of the triangle would be line segment BC according the the Angle Relationship Theorem.
300
Solve is this a triangle 8,1,6
8+1>6
1+6>8
8+6>1
No.
300
This theorem is the same as the Hinge Theorem but it uses sides to prove angle measures.
Converse of Hinge
400
What does the angle bisector theorem say with this figure.
If you add a point E between AD it turns into the angle bisector than BE is congruent to CE.
400
An order to find the measure of an altitudes what formula do you use to find the measure.
You would use A=bh/2 to find the measure of the altitudes height.
400
if you had a triangle that had 3 measures inside and one on the outside. Solve for measure 4 using these measures.
m<1- 75
m<2- 35
m<3-70
M<4 - 110 because of the Exterior Angle theorem.
M<4= m<1+m<2
400
Solve using 3rd Side 7,9,X
7+9>X
16>X or X<16
One Answer- 2<10<16
X=10
400
The Converse of Hinge is similar to one of triangle concurrency. Which one is it?
SSS- Side-Side-Side
500
Using the pythagorean theorem solve for c if A=3 and B= 4
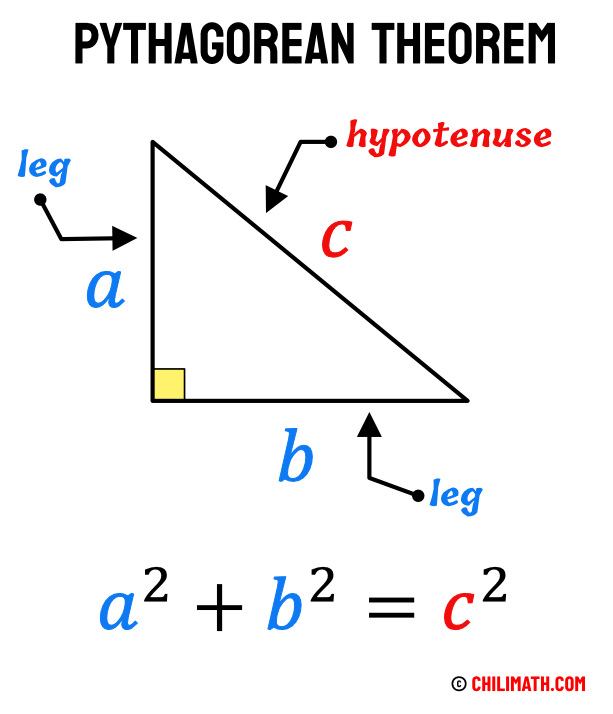
a2+b2= c2
32+42 = c2
9+16=c2
25=c2
Therefore 5 = c
500
When using the centroid theorem there is two different regions of the triangle how do you know which amount to divide by.
You know by looking at the centroid if the line segment that you are using is below the centroid than divide by 1/3 and if it is above than 2/3.
500
Using the figure name all side and angles from Largest to Smallest
Sides- Angles-
CE <D
DC <E
DE <C
500
Solve Using 3rd Side 130,X,54
130+54=184
184>X<184
130-54=76
x>76 / x<184
Answer- 184>X<76
500
Solve Using Converse Hinge
Triangle 1- ABC
Triangle 2-DEF
If: AB=DF
AC= DE
BC< FE
Them:
<A < <D