5.1 Intro to Probability Distributions
5.2 Binomial Probability Distributions
5.3 Intro to Normal Distributions
5.4 Finding Probabilities in the Normal Distributions
5.5 Finding Values from Probabilities in the Normal Distributions
100
Is the following random variable discrete or continuous? Explain why.
The temperature of the water in the Arabian Gulf
Continuous, it is measurable.
100
The probability of success in a given binomial distribution is 0.37. What is the probability of failure?
1-0.37=0.63
100
What is the area under the curve of all normal distributions?
1
100
Assume the random variable x is normally distributed with a mean of 12 and a standard deviation of 2.3. Find P(x<10).
P(Z<-0.87)=normalcdf(-10, -0.87, 0, 1)=0.192
100
Find the z-score that corresponds to the 20th percentile.
InvNorm(0.2)=-0.842
200
Determine the probability distribution's missing probability value.
0.185
200
It is known that 45% of college students are happy that they took a statistics class in high school. If you randomly selected 300 college students, what is the probability that exactly 125 of them are happy that they took a statistics class in high school? Round to three decimal places.
binompdf(300, 0.45, 125)= 0.024
200
Find the area under a normal distributoon between z=-2.15 and z=0.42
normalcdf(-2.15, 0.42, 0, 1)=0.647
200
Assume the random variable x is normally distributed with a mean of 12 and a standard deviation of 2.3.
Find P(8<x<13.5)
P(-1.739<x<0.652)=normalcdf(-1.739, 0.652, 0, 1)=0.712
200
Find the z-score that has 20.7% of the distributions area to its right.
1-0.207=0.793
invNorm(0.793)=0.817
300
Given the following probability distribution, what is the expected value?
2.12
300
The following probability distribution shows the number of households with 2 or more TVs in their house.
p=0.54 and n=7.
If 7 households are chosen at random, what is the probability that at least 4 of them have 2 or more TVs?
0.587
300
Find the are under a normal distribution to the right of z-1.54.
normalcdf(-1.54, 10, 0, 1)=0.938
300
The number of students in each class at a school is normally distributed with a mean of 20.2 and a standard deviation of 1.7
Find the probability that a randomly selected classroom will have less than 17 students.
Z-score for 17: -1.882
Normalcdf(-10, -1.882)= 0.03
300
The grades on a recent test are normally distributed with a mean of 75.9 and a standard deviaiton of 8.6.
Find the test grade that corresponds to a z-score of z=2.5
2.5=(x-75.9)/8.6
x=97.4
400
A probability distribution has a variance of 1.234. What is its standard deviation? Round to three decimal places.
1.111
400
The probability that a student plays a musical instrument is 0.34. Assume you are looking at a sample of 5 students. Using a binomial distribution, what is the probability that at least three of the students don't play a musical instrument.
0.78
400
Find the area under a normal distribution to the left of z=0.
0.5 since normal distributions are symmetric around the mean (mean=z score of 0)
400
The number of students in each class at a school is normally distributed with a mean of 20.2 and a standard deviation of 1.7.
Find the probability that a randomly selected class will have between 20 and 23 students in it.
Z-score for 20: -0.118
Z-score for 23: 1.647
normalcdf(-0.118, 1.647)=0.497
400
Find the z-score such that has 50% of the distributions area lies between -z and z.
50% in between means 25% on each side
invNorm(0.25)=-0.674
So -0.674 and 0.674
500
Given the information in the probability distribution below, calculate the variance.
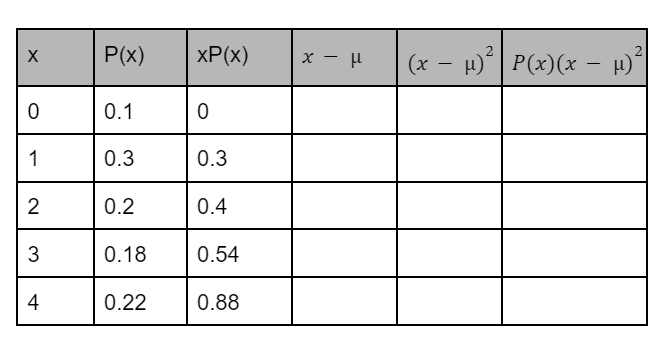
1.744
500
The probability of Mr. Gouge wearing a blue shirt on a given day is 33%. Find the mean, variance, and standard deviations for the number of days that Mr. Gouge wears a blue shirt during a 5 day school week.
n=5, p=0.33, q=0.67
Mean=np=5*.33=1.65
Variance=npq=1.106
Standard deviation=SQRT(npq)= 1.051
500
Find the area under a normal distribution to the right of z=2.1 or to the left of z=-2.1.
normalcdf(2.1, 10, 0, 1)=0.018
0.018*2=0.036
500
The number of students in each class at a school is normally distributed with a mean of 20.2 and a standard deviation of 1.7.
Find the probability that a randomly selected class has more than 24 students in it.
If a school has 100 classes happening at one time, how many of these classes would you expect to have more than 24 students in it?
z-score for 24: 2.235
normalcdf(2.235, 10)=0.013
0.013*100= 1.3 classes
500
The average height of a group of students is 1.6 meters with a standard deviation of 0.2 meters. What height represents the 60th percentile.
Z-score of 60th percentile: invNorm(0.6)= 0.253
0.253=(x-1.6)/0.2
x=1.651