Solve.
tan30o
1/√3
If the related acute angle is 33o, what would be the standard position angle in quadrant 3?
213o
Solve.
sin30o
1/2
Determine the number of triangles that could be drawn with the given measures.
In JKL, K = 45o, k = 11.5 cm and j = 7.7cm
S2 > S1
1 triangle
The sun is 62 degrees above the horizon. A tree casts a shadow that is 12 feet long. How tall is the tree?
26.2 feet
Solve.
sin315o
-1/√2
In which quadrant(s) would cosecant be positive?
Q1 and Q2
Solve.
cos240o
-1/2
A triangle has 2 sides of 230 m and 360 m, and the angle between these sides measures 38o. Find the length of the last side, to the nearest metre.
818 meters
A man flies a kite and lets out 100 feet of string. The angle of elevation of the string is 52 degrees . How high off the ground is the kite?
78.8 ft
Given (12, 5) is a point on the terminal arm with angle x. Find the value for r and then give the primary ratios for this terminal arm.
r = 13
sinx = 5/13
cosx = 12/13
tanx = 5/12
What is the tangent ratio given that alpha is angle A?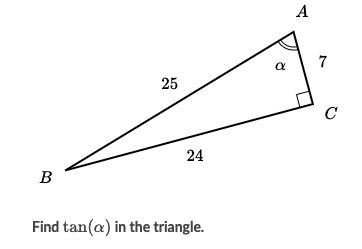
24/7
Given (-4, -3) is a point on the terminal arm with angle x. Find the value for r and then give the primary ratios for this terminal arm.
r = 5
sinx = -3/5
cosx = -4/5
tanx = 3/4
A triangle has 3 sides with a measure of a = 55 cm, b = 26 cm, and c = 32 cm.
What is the value for angle A? Round to the nearest degree.
A = 143o
Two forest fire towers, A and B, are 20.3 km apart. From tower A, the bearing of tower B is 70o. The ranger in each tower observes a fire and radios the bearing of the fire from the tower. The bearing from tower A is 25o and from tower B is 345o. How far, to the nearest tenth of a kilometre, is the fire from each tower?
Tower A = 31.5 km
Tower B = 22.3 km
Given cosx = -1 solve for x if -360o ≤ x ≤ 360o
x1 = 180
x2 = -180
Solve for x, if 0o < x < 360o
2√2cosx = 2
x1 = 45o
x2 = 315o
Given tanx = -1 solve for x if -180o ≤ x ≤ 540o
x1 = 135
x2 = 315
x3 = 495
x4 = -45
Given ∆ABC, where A = 38o, a = 7.7 cm, b = 10.5 cm
a. How many triangles are possible?
b. Solve ∆ABC. Round angles to the nearest degree and sides to the nearest hundredth of a cm.
a. 2 triangles
b. B1 = 57o
C1 = 85o
c1 = 12.45 cm
B2 = 123o
C2 = 19o
c2 = 4.07 cm
The observation deck of the Skylon Tower in Niagara Falls, Ontario, is 166 m above the Niagara River. A student, who is standing in the observation deck, notices two boats on the water. From the student’s position she can tell that boat A is at an angle of depression of 40° and boat B is at an angle of depression of 34°. The two boats are separated by an angle of 70° at the base of the tower. Calculate the distance between the two boats to the nearest metre.
257.7 m
Prove the identity.
1 - cos2x = (sinxcosx)/cotx
RS
(sinxcox)/(cosx/sinx)
sin2x
1 - cos2x
A 5 m stepladder propped against a classroom wall forms an angle of 30o with the wall. Exactly how far is the top of the ladder from the floor? Express your answer in radical form.
(5√3)/2 m
Prove the identity.
secx cosx + secx sinx = 1 + tanx
cosx/cosx + sinx/cosx = 1 + tanx
1 + tanx = 1 + tanx
Two forest fire stations, P and Q, are 20.0 km apart. A ranger at station Q sees a fire 15.0 km away. If the angle between the line PQ and the line from P to the fire is 25o how far, to the nearest tenth of a kilometre, is station P from the fire?
h = 8.5 km
h < S2 < S1
.: 2 triangles (Check both solutions)
F1 = 34o
F2 = 146o
Q1 = 121o
Q2 = 9o
q1 = 30.4 km
q2 = 5.6 km
A sailor out in a lake sees two lighthouses 11 km apart along the shore and measures the angle from his present position between lighthouse A and lighthouse B to be 48°. From lighthouse B, lighthouse A and the sailor has an angle of 45°. How far to the nearest kilometer is the sailor from both lighthouses?
b = 10.47 km
a = 14.78 km