Conditional Probability
Independent and Dependent Events
Mutually Exclusive Events
Combinations and Permutations
Law of Large Numbers
1
What is the formula for Conditional Probability?
1
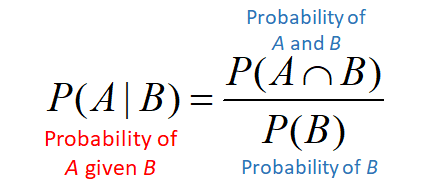
P(A)=P(B)
Independent.
When the probability of one event does NOT change the probability of a second event.
1
What are mutually exclusive events?
When two or more events cannot happen at the same time.
1
What is this?
Permutation Lock
1
What is the Law of Large Numbers?
The more trials (experiments) we do, the closer our experimental data (results) approach our theoretical data (what should happen).
2
Conditional Probability places a condition on all original possible outcomes. What do we call the remaining possible outcomes?
Subset
2
A bag has 7 marbles (4 blue, 3 red). You pick a blue marble, replace it. You pick another blue marble.
Independent.
The probability of drawing the second blue marble did not change because of drawing the first blue marble.
2
You roll a 6 sided die.
P(4 OR an odd number) =
1/6 + 3/6 = 4/6 or 2/3
2
How can I differentiate between combinations and permutations?
Permutations - Order Matters
Combinations - Order Doesn't Matter
2
Why do teachers encourage you to retake a test/quiz?
Law of Large Numbers states that if you repeat something enough times, what your results are will approach what you want.
In this case, you want a better score on the test/quiz.
3
You roll a 6 sided die.
P(4|# greater than 1)
1/5
3
The probability of you passing your Unit 6 Test increased because you studied.
Dependent.
Anytime the probability changes due to an event, it's a dependent event.
3
You have 18 fish in a fish tank. 8 are solid colored, 4 are spotted, and 6 are striped.
What is the probability that you select a solid fish or a striped fish?
P(solid OR striped) = 8/18 + 6/18 = 14/18
14/18 = 7/9
3
What does "n" refer to?
What does "r" refer to?
n = All possible things to choose
r = The amount we actually choose
3
You spin a spinner 8 times.
Observed P(yellow) = 0.875 or 87.5%
Predicted P(yellow) = 0.250 or 25%
Why is our prediction wrong?
We need to spin the spinner more. 8 spins wasn't a large enough sample size.
87.5% is not close to 25%
4
P(Jack | NOT a Club)
1/13
4
I pass out one card to each student from a full deck of cards. Describe each instance of my passing out one card.
Dependent.
If I pass out any one card, the probability that the next card is the exact same one I JUST passed out is now 0.
4
In a deck of 52 cards, what's the probability of randomly selecting a 3 or a double-digit card?
8/52
2/13
4
You're almost out of time with your Unit 6 Test! You have 6 blanks left to answer and only have time to answer 2 of them. How many ways can you answer questions with the time you have left?
15
nCr (6,2) = 15
4
We spun the spinner 800 times.
Observed P(yellow) = 0.246 or 24.6%
Predicted P(yellow)= 0.250 or 25%
Should we keep spinning the spinner?
No, because the relative frequency of the observed outcomes (0.246) is VERY close to the predicted frequency of outcomes (0.250), we can conclude that 800 spins is a large enough number.
5
P(Jack | Face Card) =
Face cards are Jacks, Queens, and Kings
1/3
5
You draw a black card out a deck of cards and do not replace it into the deck.
You separate out all of the black cards and red cards and draw a diamond out of the stack of red cards.
Independent.
Both events have a probability of 1/2. Even though we did not replace the black card, it did not affect the outcome of the second event.
5
Last year, my roster listed 43 students as male.
Last year, my roster listed 57 students as female.
What is P(Male cup Female)?
100/100
1
5
Your "red day" classes next year will be English, History, Art, and Science. How many ways can the schedule makers make your red day schedule?
24
nPr (4,4) = 24
5
Take a shot for 5 points.
No doubling.
