Growth and Decay
Graphs Galore
Mix it Up!
Lots of Logs
Exciting Exponentials
100
In the equation below, what does P represent?
A = Pe^(rt)
Principal or initial amount.
100
What is the domain for ALL exponential functions?
All real numbers.
(-oo,oo)
(The fancy R)
100
Which properties of logarithms are being used below?
5ln(x)-ln(3)=ln(x^5/3)
Quotient and Power
100
State the equality property. What does the equality property of logs allow us to do?
If log(x) = log (y), then x = y.
If two logs have the same base are set equal to each other, we can say their inner terms are also equal.
100
Identify the base of
8(1/2)^(y
1/2
200
In the equation below, the value of b tells us if the function is exponential growth or exponential decay. When b is ____, the function is growth. When b is ____, the function is decay.
f(x)=a(b)^x
Blank 1: larger than 1
Blank 2: in between 0 and 1
200
What is the range of the graph shown? Use interval notation!
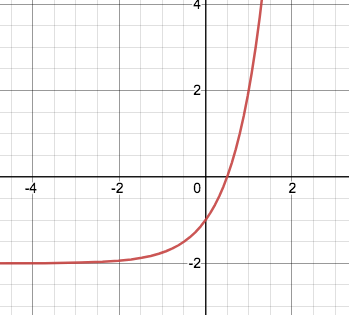
(-2,oo)
200
What is the name of e? State the value of e rounded to two decimal places.
Euler's Number
e=2.72
200
Expand the log completely.
log((y^7z^3)/(100x))
(7logy+3logz)-(2+logx)
200
What makes an exponential function special compared to all other function families we have studied this year.
(hint: think of the variable's location)
The variable is in the exponent!
Bonus points if quick growth is mentioned.
300
I deposit $300 into an account that compounds weekly at a rate of 6.3%. How much will be in my account in 15 years?
SHOW ALL WORK
$771.40
300
Define a horizontal asymptote.
A horizontal line that a graph approaches but never touches or crosses.
300
Evaluate the following logs.
ln(1)
log(10)
ln(1)=0
log(10)=1
300
Condense the log completely.
(ln(3)+16ln(x))-ln(y)
ln((3x^16)/y)
300
Write the log in exponential form.
ln(3x)=12
e^12=3x
400
How long will it take for $2000 to become $3000 in an account that is compounded continuously at a rate of 9%? Round your answer to the nearest tenth.
SHOW ALL WORK and DON'T FORGET UNITS
4.5 years
400
Where is the horizontal asymptote of
y = 2(1/3)^(x+1)-6
y = -6
400
Solve for x. Round to the nearest tenth. SHOW ALL WORK
3e^x-7=14
x = 1.9
400
Solve for x. SHOW ALL WORK
log(x^2-3)=log(13)
x=-4,4
400
Solve for x. Leave your answer as a fraction and SHOW ALL WORK!
5^(4x-9)+125=15750
x=15/4
500
A population of bacteria triples every day. The initial population is 300 bacteria. How many bacteria will be present in 4 days? How many days until the population reaches 12,000,000 (round to the nearest tenth)? SHOW ALL WORK and DON'T FORGET UNITS
(Hint: convert days to hours)
4 Days: 24,300 bacteria
12,000,000 Bacteria: 9.6 days
500
Graph the following using a table of three points. Be sure to show the horizontal asymptote clearly!
y = 2^(x-1)+3
500
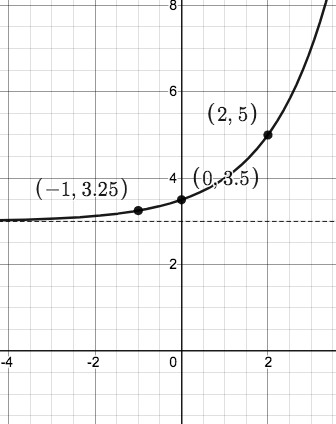
Solve for x. Round to the nearest tenth. SHOW ALL WORK
ln(x)+ln(4)=ln(12)
x = 3
500
Solve for x. SHOW ALL WORK
log(5)+log(x)-12=-10
x=20
500
Solve for x. SHOW ALL WORK
3(20^x)+1=4
x=0