Find the period, amplitude, max, and min of the following function:
f(x) = -2sin(pi/2x + 3) - 1
Period: 4
Amplitude: 2
Max: 1
Min: -3
Find x.
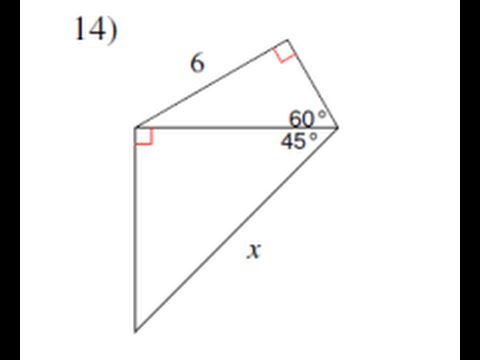
x = 4sqrt6
Evaluate:
cos(-270^o)
0
The height of a point, in inches, on a wheel can be modeled with the function below, where t is the number of seconds the wheel has been revolving. How long does it take that point to make a full revolution on the wheel?
f(t) = -2sin(3pit + 2) + 2
2/3 seconds
San Antonio, Texas, is located 30 degrees north of the equator. If Earth's radius is about 3959 miles, about how many miles is San Antonio from the equator?
2073 miles
Name the period and repeating asymptote equations of the following function:
f(x) = 3/2tan(2x) + 3
period:
pi/2
asymptote:
x = pi/4 + pi/2n
The point (-3, 4) is on the the terminal side of an angle,
theta
. Find
sec(theta)
-5/3
Evaluate
tan((17pi)/6)
-sqrt3/3
Create an equation of the graph with the starting point in blue:
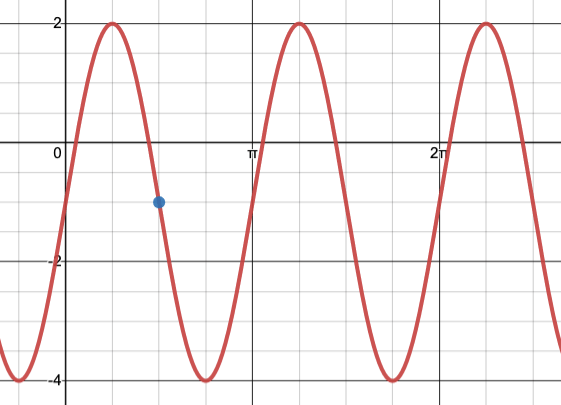
f(x) = -3sin[2(x - pi/2)] - 1
f(x) = -3sin(2x - pi) - 1
You are riding a bicycle which has tires with a 26-inch diameter at a steady 15 miles per hour. What is the angular velocity of a point on the outside of the tire in radians per second? [1 mile = 5280 feet]
20.3 radians/second
Transform the following coordinates from their parent function:
(0, 1), (pi/2, 0), (pi, -1), ((3pi)/2, 0), (2pi, 1)
f(x) = 1/2cos(pix - pi/2) + 3
(1/2, 7/2), (1, 3), (3/2, 5/2), (2, 3), (5/2, 7/2)
If
0<theta<2pi, sin(theta) = sqrt3/2, cos(theta) = -1/2
find
theta (radians)
(2pi)/3
Evaluate:
sin(1035^o)
-sqrt(2)/2
Create a tangent equation that has asymptotes at
x = -pi/6, pi/6
and goes through the points
(0, -1) and (pi/12, -2)
y = -tan(3x) - 1
Your bike has a wheel diameter of 30 inches. You are riding and your wheels are rotating at 141 revolutions per minute. What is the bicycle speed in miles per hour? (5280 feet = 1 mile) Round to nearest hundredth
12.58 mph
What is the "starting point" of the following function (the transformed coordinate of x = 0 from the parent function)?
f(x) = -3/2cos(1/2x - 6) - 4
(12, -11/2)
If
cot(theta) = 7/5
and
sin(theta) < 0
find
csc(theta)
-sqrt(74)/5
Evaluate:
csc(7pi)
undefined
The center of an analog clock that is hung on the wall is 15 feet high. The clock has a second hand that is 1 foot long. What is the height of a point on the end of the second hand when it is three seconds past the 9? Round to the nearest tenth.
15.3 seconds
Memphis, TN, and New Orleans, LA, lie on the same longitude line. Memphis has a latitude of 35 degrees North and New Orleans has a latitude of 30 degrees North. Find the distance between the two cities if the radius of the earth is 3960 miles.
345.575 miles
Write the period and the repeating asymptote equation of the following function:
f(x) = -2tan(1/3x - pi/4) + 5
period:
3pi
asymptote equation:
x = (9pi)/4 + 3pin
If
sec(theta) = (2sqrt3)/3
and.
tan(theta) < 0, 0<theta<2pi
find
theta (radians)
(11pi)/6
Evaluate:
sec((7pi)/6)
-(2sqrt(3))/3
Write the equation of tangent that goes through the points
((3pi)/4, 1), ((5pi)/4, -1), ((7pi)/4, -3)
f(x) = -2tan[1/2(x - (5pi)/4)] - 1
f(x) = -2tan(1/2x - (5pi)/8) - 1
A carousel at the county fair makes 3 revolutions per minute. People riding horses on the outside are traveling about 7.069 feet/sec. People riding horses on the inside are riding about 3.1 feet/sec. How much farther away from the center are people on the outside horses?
about 12.6 feet