General Sequences and Series
Arithmetic Sequences
Geometric Sequences
Arithmetic Series
Geometric Series
100
What is the difference between a sequence and a series?
A sequence is an ordered list of numbers, whereas a series is the sum of a given number of terms in a sequence.
100
Write the formula for the given arithmetic sequence:
-2, 2, 6, 10, 14, ...
an = -2 + (n-1) 4
or
an = 4n - 6
100
For the given sequence, find the common ratio
1/2, 2, 8, 32, ...
r = 4
100
Evaluate the given series.
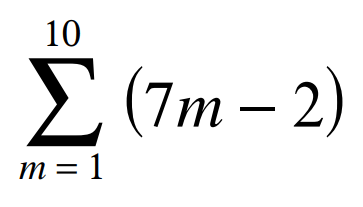
S10 = 365
100
Evaluate the given series:
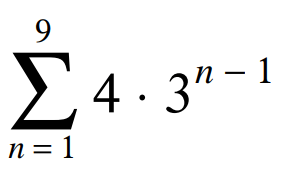
S9 = 39,364
200
What is the difference between an arithmetic and a geometric sequence?
An arithmetic sequence is a sequence that has a common difference (the same number gets added each time).
A geometric sequence is a sequence that has a common ratio (the same number gets multiplied each time).
200
Given that a1 = 7 and the common difference is -2, find a6
a6 = -3
200
Write the formula for the given geometric sequence:
32, 16, 8, 4, ...
an = 32 (1/2) n-1
200
Find the sum of the first 5 terms of the arithmetic sequence:
an = 2n + 1
35
200
Is the following a geometric series?
3 + 12 + 21 + 30, ...
No, it is arithmetic.
300
What is the next number in the pattern?
1, 1, 2, 6, 24, ?
120
300
For the given sequence, find the common difference and the 10th term.
9, 12, 15, 18, ...
d = 3
a10 = 36
300
Given that a1 = 3 and r = 2, find a6.
a6 = 96
300
Find the sum of the arithmetic series:
a1 = 42, an = 146, n = 14
1316
300
Find the sum of the first 5 terms of the geometric series: an = -2(0.25)n-1
Answer as a fraction please.
-341/128
400
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ... is the _____________ sequence.
Fibonacci
400
Find n, the number of terms in the arithmetic sequence.
-2, 1, 4, 7, ... , 70
n = 25
400
Given the formula for the geometric sequence, list out the first 5 terms:
an = (-2)-n
-1/2, 1/4, -1/8, 1/16, -1/32
400
What is the sum the integers from -10 to 90?
4040
400
Find the sum of the infinite geometric series:
-2, -2/3, -2/9, -2/27, ...
-3
500
Write a formula for the given sequence:
-2, 6, -18, 54, ...
an = -2(-3)n-1
500
Does this infinite arithmetic series have a finite sum? Explain why or why not.
2 + 12 + 22 + 32+ 42 + 52 ...
No. The series diverges which means it keeps getting bigger without bound.
500
Given a3 = 16 and a7 = 1/16, find the common ratio.
1/4
500
The sum of the odd integers from 1 to 100
2500
500
The sum of a finite geometric series with a common ratio of 3 is -728. Find a1.
-2