Chain Rule
Euler's Number
Natural Logs
Slopes & Tangent Lines
Tables of Chain Rule
100
d/dx(4x^3+2)^7=
7(4x^3+2)^6(12x^2)
100
d/dxe^(8x)=
8e^{8x}
100
d/dxln(4+5x)=
5/(4+5x)
100
Evaluate the derivative of f(x) at x = 1
f(x)=(-2x)/e^(3x)
\frac{4}{e^3}
100
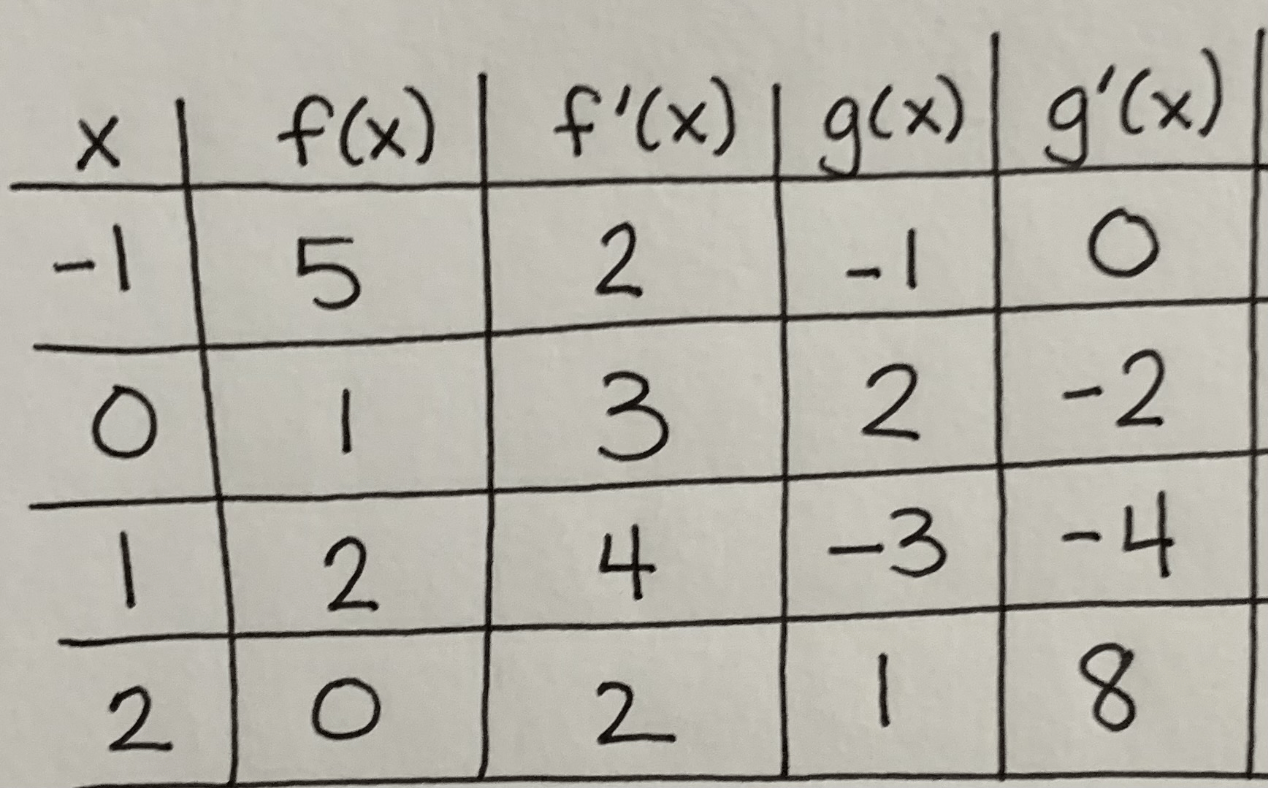If h(x)=f(g(x)), find h ' (0)
-4
200
d/dx(3\cdot sqrt(7x+1))=
\frac{3}{2}(7x+1)^{-\frac{1}{2}}(7)
200
d/dx5(e^(2x)+1)=
10e^{2x}
200
d/dxlnsqrt(4+5x)=
1/2*5/(4+5x)
200
Evaluate the derivative of f(x) at the point x = -2.
f(x)=3ln(1-x)
-1
200
If h(x)=g(f(x)), find h ' (0)
-12
300
d/dx [5x(3x-1)^4]=
5(3x-1)^4+4(3x-1)^3(3)(5x)
300
d/dxe^(2x)Sin(3x)=
2e^(2x)(sin3x)+(cos3x)(3)(e^{2x})
300
d/dxcos(lnx)=
-1/x*sin(lnx)
300
What is the slope of the line tangent to the graph of f(x) at the point where x=pi/4?
f(x)=ln(3sinx)
1
300
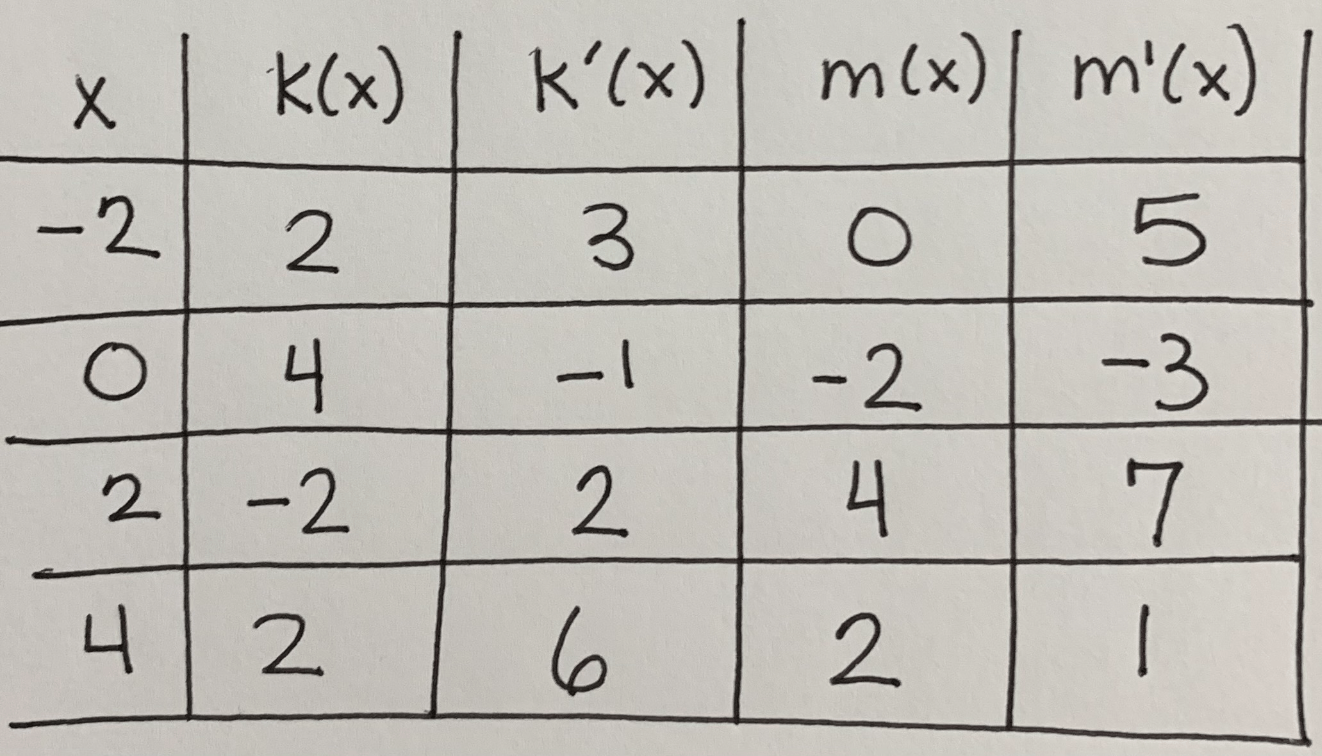If p(x)=k(m(x)), find p ' (-2)
-5
400
\frac{d}{dx}4cos^2(3x)=
8(cos3x)(-sin3x)(3)
400
Differentiate and simplify your result:
d/dx(x^3e^x-xe^x)=
e^x(3x^2+x^3-1-x)
400
d/dxx^2ln(4x+3)=
2xln(4x+3)+\frac{4}{4x+3}(x^2)
400
What is the equation of the line tangent to f(x) where x=0?
f(x)=3e^-x-1
y-2=-3(x-0)
400
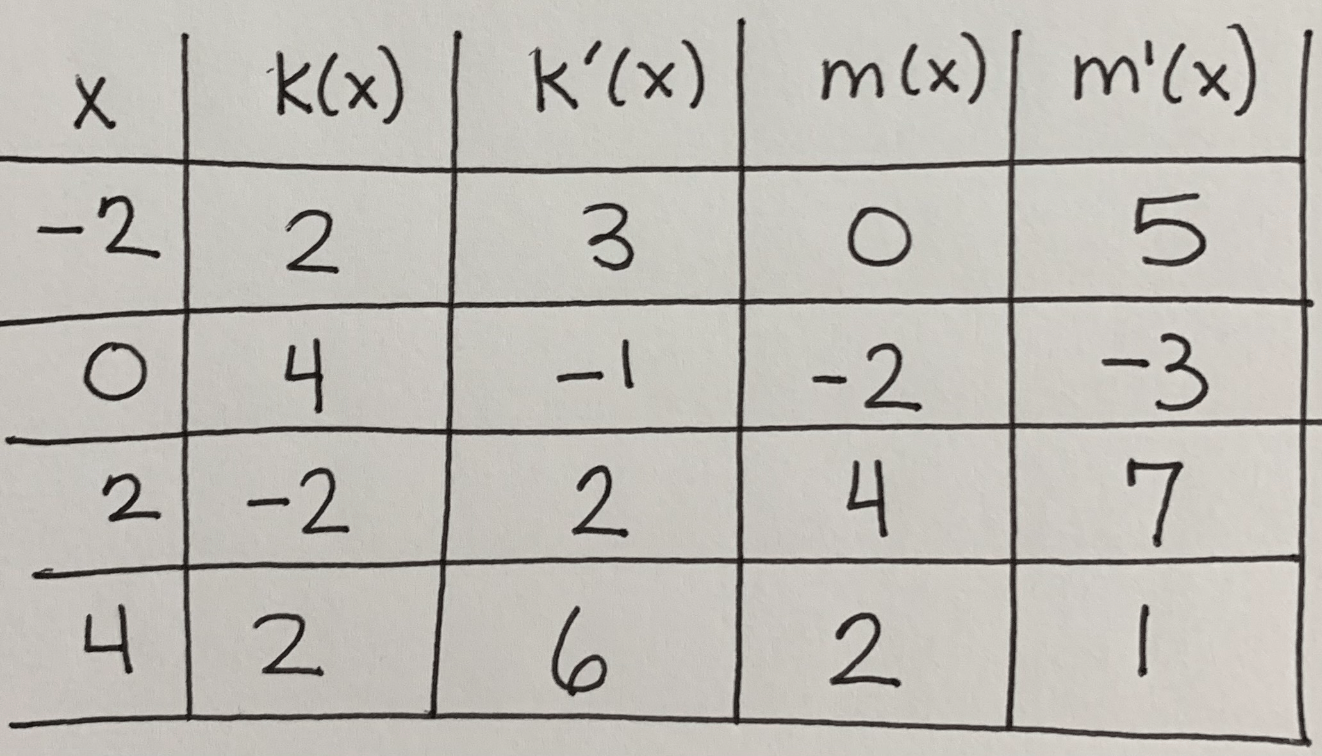If p(x)=m(k(x)), find p ' (-2)
21
500
\frac{d}{dx}5xsin^2(\pix)=
5(sin\pix)^2+2(sin\pix)(cos\pix)(\pi)(5x)
500
Differentiate and simplify your result:
d/dx(e^x+2)/(e^-x+1)=
(e^x+2e^-x+2)/(e^-x+1)^2
500
d/dxln(sec(2x)+tan(2x))
(2sec(2x)tan(2x)+2sec^2(2x))/(sec(2x)+tan(2x))
500
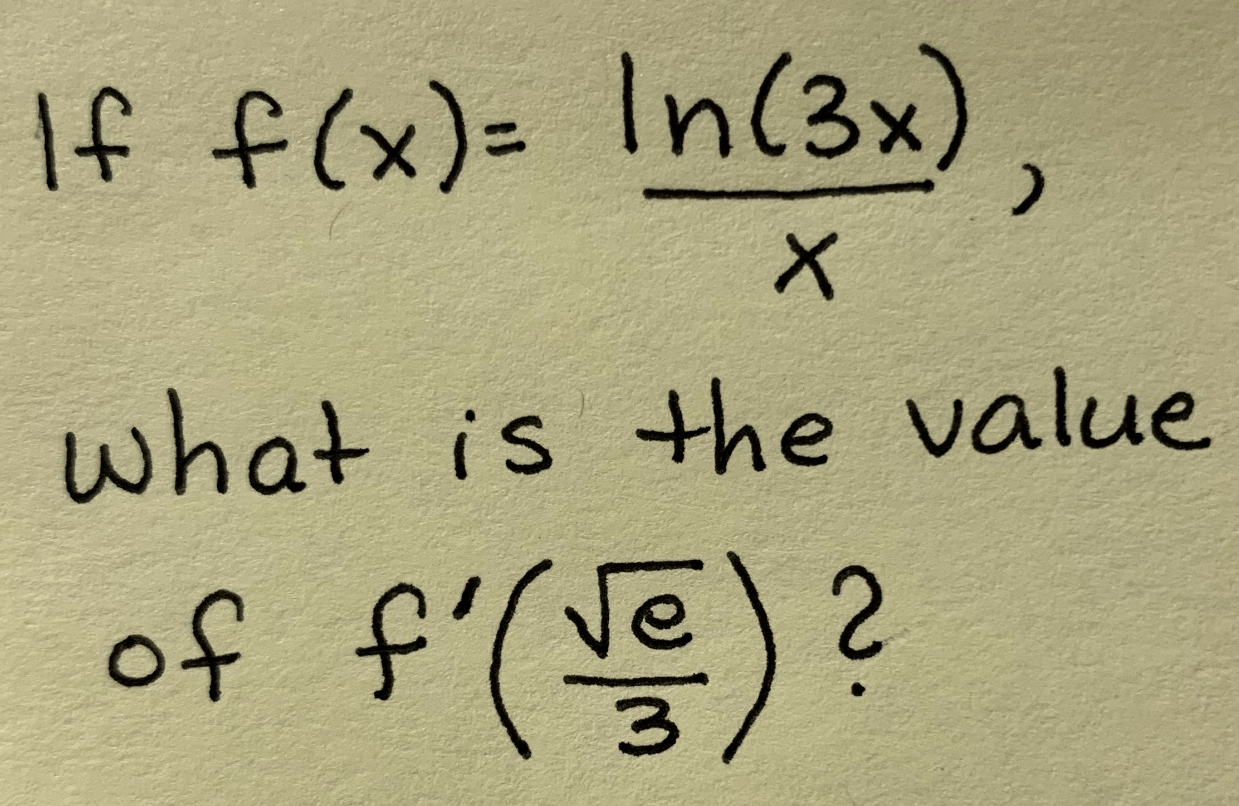
9/(2e)
500
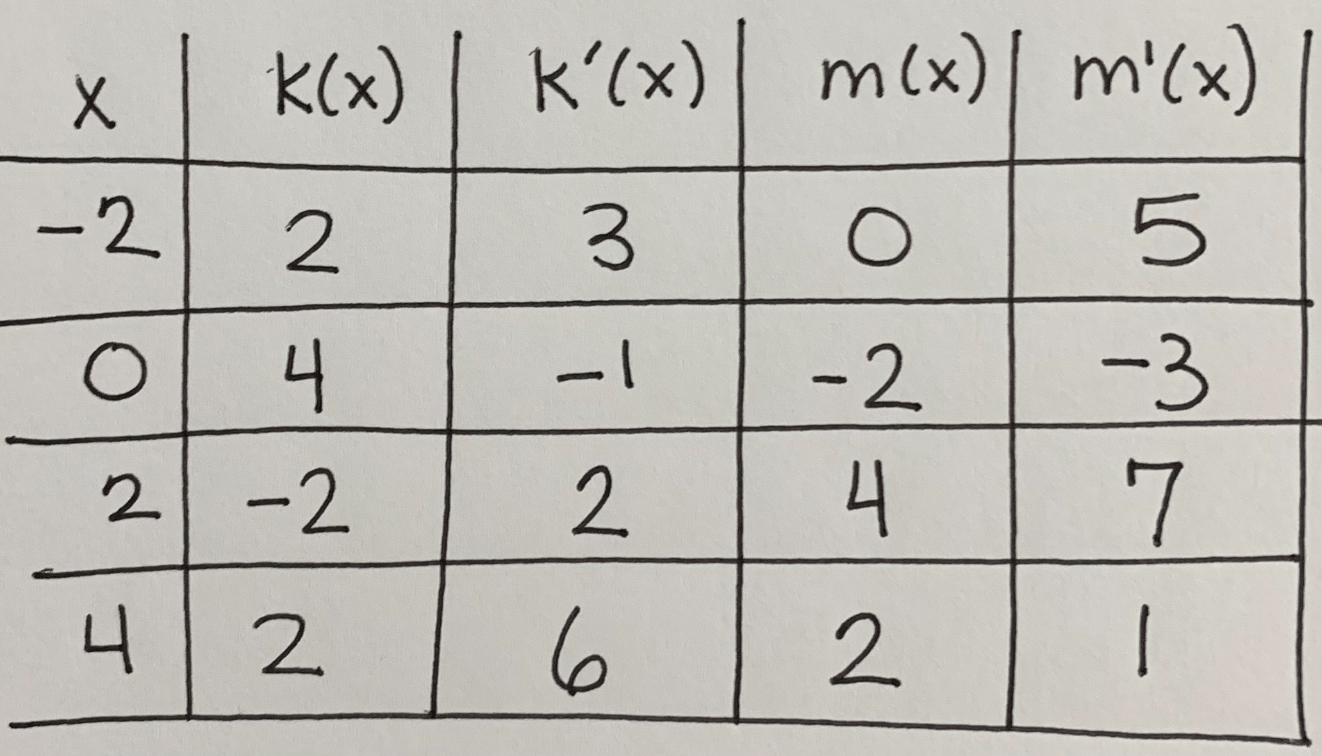If p(x)=m(m(x)), find p ' (4)
7