Theoretical Probability of Simple Events
Identifying Independent or Dependent Events
Theoretical Probability of Compound Events
Experimental Probability of Simple Events
Experimental Probability of Compound Events
Counting Principle and Tree Diagrams
Miscellaneous Probability Problems
100
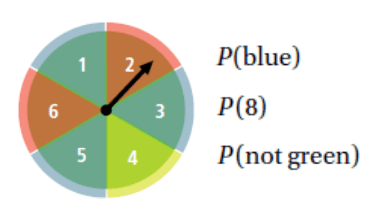
1. 3/6 = 1/2
2. 0
3. 5/6
100
tossing four fair coins
INDEPENDENT
100
You roll a fair number cube. Find probability:
1. Are the events above independent or dependent events?
2. P(3 and then 5)
1. independent
2. 1/36
100
14/40=7/20
100
1. What is the experimental probability that the next sample will be regular vanilla?
2. What is the experimental probability that the next sample will be strawberry?
3. What is the experimental probability that the next sample will not be peach?1. 19/200; 2. 85/200=17/40; 3. 136/200=17/25
100
A travel agent plans trips for tourists from Chicago to Miami. He gives them three ways to get from town to town: airplane, bus, train. Once the tourists arrive, there are two ways to get to the hotel: hotel van or taxi.
1. Use the counting principle to determine the number of outcomes.
2.Draw a tree diagram to illustrate the possible choices.
100
To set a password, you must select 3 numbers from 0 to 9. Each number may be used more than once?
1. Are the events above independent or dependent events?
2. How many possible passwords are there?
1. independent
2. 1000 passwords
200
DOUBLE JEOPARDY
1/8
200
pulling a white sock from a box,
not replacing it, and then pulling
a black sock on the second pull
DEPENDENT
200
A box contains fifteen billiards balls, numbered 1 through 15. Anna draws a ball, records the number, and then returns it to the box. Then Vicki draws a ball. Find probability.
1. Are the events above independent or dependent events?
2. P(8, and then odd)
1. independent
2. 8/225
200
28/55
200
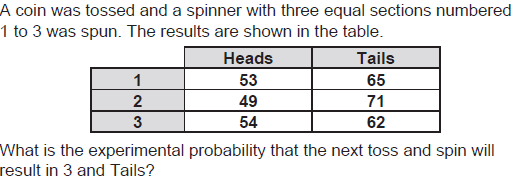
62/354=31/177
200
A choice of pizza or spaghetti; a choice of milk or juice to drink; a choice of pudding or an apple for dessert
1. Use the counting principle to determine the number of outcomes.
2.Draw a tree diagram to illustrate the possible choices.
200
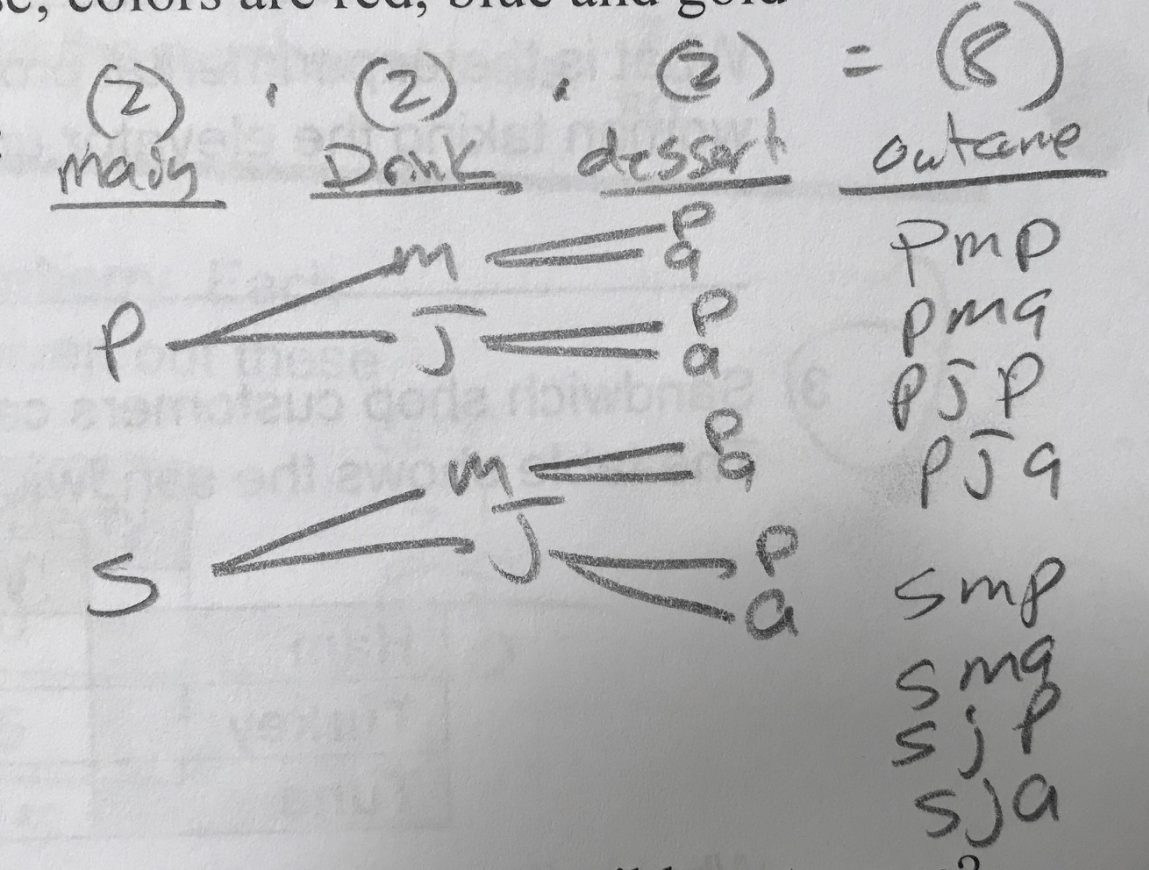
A park has about 500 trees. You find that 27 of 67 randomly chosen trees are oak trees. About how many trees in the entire park are likely to be oak trees?
1. Write a proportion and solve
27/67 = x/500; about 201 oak trees
300
16/25
300
DOUBLE JEOPARDY
a spinner and a fair number cube
are used in a game
INDEPENDENT
300
Each letter of L I T T R E L L is written on a card. The cards are placed in a basket. Find each probability if Elsa selects a card, leaves it out, and then selects another card.
1. Are the events above independent or dependent events?
2. P(T, and then E)
1. dependent
2. 1/28
300
At a city hospital, 40 boys and 50 girls were born yesterday. What is the experimental probability that the next baby born will be a girl?
50/90=5/9
300
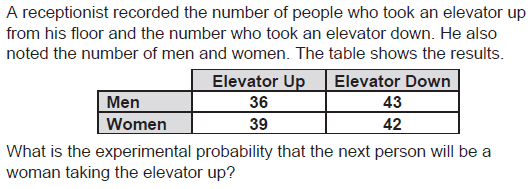
39/160
300
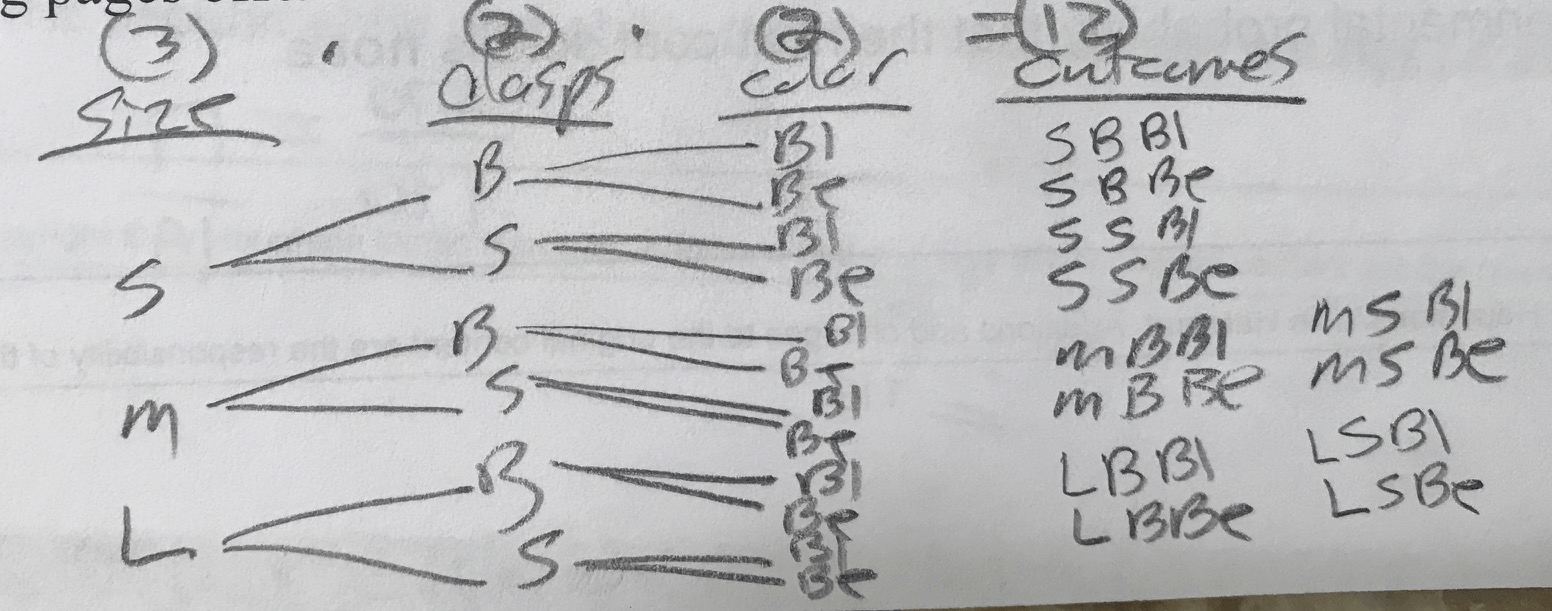
Shirts come in three sizes: small, medium or large; shirts have buttons or snaps; colors are blue or beige.
1. Use the counting principle to determine the number of outcomes.
2.Draw a tree diagram to illustrate the possible choices.
300
DOUBLE JEOPARDY
A special deck of cards consists of 5 red cards, 20 blue cards, and 25 green cards. Catherine selects 1 card from the special deck 500 times. How many times can she expect to draw a red card?
1. Write a proportion and solve
5/50=x/500; 50 red cards
400
A spinner has 3 red and 5 blue sections of equal size. A friend says the odds in favor of spinning blue are 3 to 5. Describe and correct the error.
It should be 5 to 8. You need to combine the red and blue sections.
400
pulling a white sock from a box,
replacing it, and then pulling a
black sock on the second pull
INDEPENDENT
400
There are 5 slices of pepperoni pizza, 1 slice of sausage pizza, and 3 slices of cheese pizza left.
Without looking, Mr. Douglas took a slice of pizza, ate it, and then took another slice.
1. Are the events above independent or dependent events?
2. What is the probability of Mr. Douglas eating two slices of cheese pizza?
1. dependent
2. 1/12
400
DOUBLE JEOPARDY
3/5
400
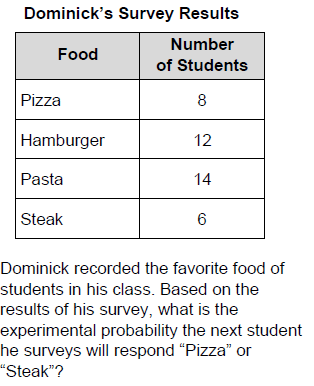
What is the experimental probability that the next sandwich sold will be tuna or turkey on wheat bread?
45/137
400
DOUBLE JEOPARDY
The choices for school mascot are lion, bear and porpoise; colors are red, blue and gold.
1. Use the counting principle to determine the number of outcomes.
2.Draw a tree diagram to illustrate the possible choices.
400
Write your own example of an independent event.
VARIES
500
The United States has a land area of about 3,536,278 mi2. Illinois has a land area of about 57,918 mi2. What is the probability that a location in the United States chosen at random is NOT in Illinois?
1. Give your answer to the nearest tenth of a percent.
2. Write answer as a fraction as well.
1. 98.4%
2. 98.4/100=24.6/25
500
placing the letters of the word
MATHEMATICAL on note
cards—a card is drawn and not
replaced before a second card is
drawn
DEPENDENT
500
DOUBLE JEOPARDY
1. Are the events above independent or dependent events?
2. P (both letters are vowels)
1. independent
2. 2/21
500
Amelia randomly picked 15 flowers from a garden. Five of the flowers she picked were tulips. What is the experimental probability that the next flower she picks will not be a tulip?
10/15=2/3
500
DOUBLE JEOPARDY
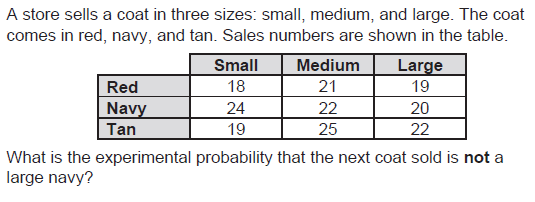
17/19
500
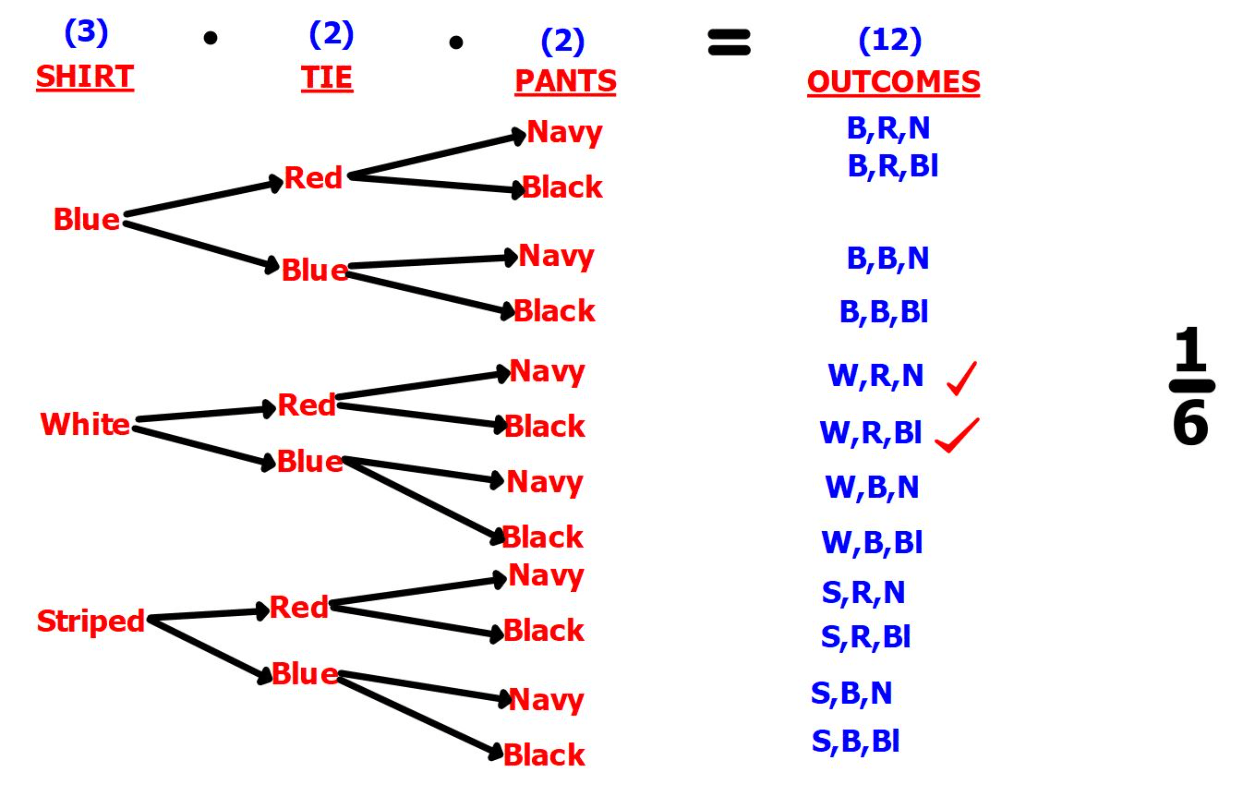
Brian must dress up for his job interview. He can wear either a blue, white or striped dress shirt; red or blue tie; and either navy or black dress pants.
1. Use the counting principle to determine the number of outcomes.
2.Draw a tree diagram to illustrate the possible choices.
3. Determine the probability of the Brian wearing a white shirt, red tie with any color dress pants?
500
Write your own example of and a dependent event.
VARIES