Terminal Points & Reference Numbers
Trigonometric Functions & Their Inverses
Physics Applications
Angle Measure & Right Triangle Trig
100
Find the y-coordinate of P(-3/5,y) if P lies on the 3rd quadrant of the unit circle.
y=-4/5
100
In which quadrant does the terminal point determined by t lie when tant>0 and cost<0 ?
Quadrant III
100
The displacement of a mass suspended by a spring is modeled by the function y=10sin(4pit) . Find the amplitude, period, and frequency.
|a|=10
p=1/2s
f=2Hz
100
Without using a calculator, find the sine of which angle equals cos(23°) .
sin(67°)=cos(23°)
200
Find the terminal points P(x,y) on the unit circle determined by t=-3pi and t=(3pi)/4 .
P(-1,0)
and
P(-sqrt2/2,sqrt2/2)
200
Find sint , cost, and tantwhen the terminal point determined by t is P(3/5,-4/5) .
sint=-4/5
cost=3/5
tant=-4/3
200
Build a function that models the simple harmonic motion having the given properties: the displacement is zero at t=0, amplitude=6in, and period= pi/4Hz .
y=6sin(8t)
200
Find the area and the arc length of a sector with a central angle
theta=45°
in a circle of radius r=4.
A=2pi
and
L=pi
300
Find the terminal points P(x,y) on the unit circle determined by t=-(5pi)/3 and t=(11pi)/6 .
P(1/2,sqrt3/2)
and
P(sqrt3/2,-1/2)
300
Find the six trigonometric functions of t=(2pi)/3 .
sin((2pi)/3)=sqrt3/2
cos((2pi)/3)=-1/2
tan((2pi)/3)=-sqrt3
csc((2pi)/3)=2sqrt3/3
sec((2pi)/3)=-2
cot((2pi)/3)=-sqrt3/3
300
Build a function that models the simple harmonic motion having the given properties: the displacement is at its maximum at t=0, amplitude=2.4m, and frequency 1/4Hz .
y=2.4cos(pi/2t)
300
Find the six trigonometric ratios of the angle
theta
in the following figure.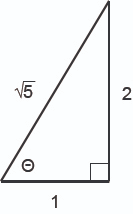
sin(theta)=2sqrt5/5
cos(theta)=sqrt5/5
tan(theta)=2
csc(theta)=sqrt5/2
sec(theta)=sqrt5
cot(theta)=1/2
400
Find the reference numbers for t=(2pi)/3 , t=-(21pi)/4 , t=-(11pi)/3 and t=(31pi)/6 .
pi/3
pi/4
pi/3
pi/6
400
Find the relationship between a) sin(-pi/6) and sin(pi/6) , b) cos(-pi/4) and
cos(pi/4) and c)
tan(-pi/3) and
tan(pi/3)
sin(-pi/6)=-sin(pi/6)
cos(-pi/4)=cos(pi/4)
tan(-pi/3)=-tan(pi/3)
400
Suppose a car tire rotates 8 times a second. The tire has a diameter of 8 inches. Find the angular and linear velocities in radians per second and inches per second, respectively.
ω=16pi
rad/s
v=64pi
in/s
400
Find sides x and y in the following right triangle.
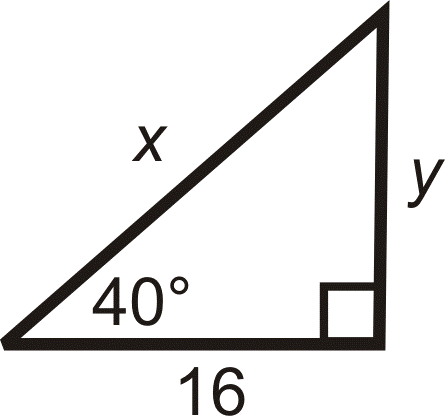
x≈20.9 and y≈13.4
500
Find the terminal points and the reference number P(x,y) on the unit circle determined by t=-(7pi)/6 and t=(13pi)/4 .
pi/6
P(-sqrt3/2,1/2)
and
pi/4
P(-sqrt2/2,-sqrt2/2)
500
Evaluate the following, if defined: sin^{-1}(sqrt2/2) , cos^{-1}(-1/2) , tan^{-1}(-sqrt3/3) , sin^{-1}(2) and cos^{-1}(0)
sin^{-1}(sqrt2/2)=pi/4
cos^{-1}(-1/2)=(2pi)/3
tan^{-1}(-sqrt3/3)=-pi/6
sin^{-1}(2)=undefined
cos^{-1}(0)=pi/2
500
A car travels at a constant speed around a track that is circular and has a circumference of 4 miles. If the car completes 8 laps in 10 minutes, what are the angular and linear velocities of the car in radians per hour and miles per hour?
ω=96pi
rad/hr
v=192
miles/hr
500
Find side j in the following triangles in its most simplified form.
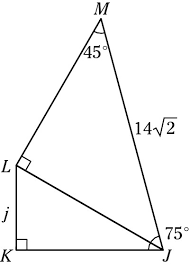
j=7