Torque and Rotational Statics
Rotational Kinematics
Rotation Dynamics and Energy
Angular Momentum
?
100
How is torque created?
By applying a non-zero net force to an object NOT at its center of mass (so it rotates)! This creates angular acceleration.
100
What are the rotational kinematic equations analogous to? Include torque and moment of inertia.
Linear kinematic equations! Substitute the variables (e.g. v/r = ω)
Force --> torque
Mass --> Moment of Inertia
100
What is the formula for rotational kinetic energy?
½ Iω²
100
What is the formula for angular momentum of a point mass?
L = mvr
100
Is this the hardest unit in AP Physics C: Mechanics?
Yes
200
When can you use these relationships?
x = rθ
v = rω
a = rα
When the object is rolling WITHOUT slipping.
200
A wheel accelerates from rest at 2 rad/s² for 5 seconds. What is its final angular velocity?
ω = ω₀ + αt
0 + 2 × 5 = 10 rad/s.
200
What is the equation definition of moment of inertia? *Think about the parallel-axis theorem?
I = I0 + md2
:max_bytes(150000):strip_icc()/MomentInertia-56fd5a985f9b586195c6d7a0.jpg)
200
A skater pulls in their arms when spinning. How does the angular velocity change?
Conservation of angular momentum
Iω = Iω
BIG I small ω = small I BIG ω
Greater ω
200
What fundamental principles do you need to think about?
net torque = Iα
Fnet = ma
Conservation of angular momentum and energy
Relationship between linear and angular motion
I = sum of mr2
300
How do you calculate net torque?
When is rotational equilibrium achieved?
Counterclockwise torque - clockwise torque
When net torque = 0
300
A spinning disk goes from 6 rad/s to 3 rad/s in 2 revolutions. What is its angular acceleration?
USE LAST EQUATION because it is the only one that doesn't have t (unknown).
2 revolutions = 4π
θ = (ω² - ω₀²) / 2α
4π = (36 - 9) / 2α
α = 27/8π = 1.075 rad/s²
Since the angular velocity decreases, it's -1.075 rad/s²
300
How does mass distribution affect rotational inertia?
The farther mass is from the center of rotation, more moment of inertia. It directly relates to the equation I = mr2.
*Think about spinning with arms open and with arms closed. You spin quicker when you close your arms.
300
A disk (I = ½MR²) of mass 4 kg and radius 0.3 m is spinning at 10 rad/s. A mass (0.5 kg) is dropped onto the edge and sticks. What is the final angular velocity?
Initial angular momentum = Iω = (0.5 x 4 x 0.32) x 10 = 1.8
1.8 = (½MR² + md2)ωf
1.8 = (0.18 + 0.5 x 0.32)ωf
ωf =1.8 / 0.225 = 8 rad/s
300
What do you do for AVERAGE net torque/angular acceleration/velocity?
Change over time (hopefully it is given)
400
A seesaw is in equilibrium with a 30 kg child sitting 2 m from the pivot. How far must a 50 kg adult sit on the opposite side to maintain balance?
30g x 2 = 50 g x d
d = 1.2 m
400
What is centripetal acceleration, tangential acceleration, and total acceleration calculated in rotational kinematics?
ac = v2/r = ωr
at = αr
atotal = sqrt(ac2 + at2)
400
How to calculate power in rotational dynamics?
P = W/t = ΔKE / t = 0.5Iω2 / t
400
A figure skater spins with arms extended, then pulls them in, reducing her moment of inertia by 40%. By what factor does her angular velocity increase?
If = I0 x 0.6
Iω = Iω
I0ω0 = 0.6I0ωf
ωf =I 0ω0 /0.6I0 =1.667ω0
400
A bullet of mass 0.05 kg strikes and embeds itself at the edge of a stationary uniform disk (mass = 2 kg, radius = 0.2 m). The bullet's speed is 300 m/s, and it hits tangentially. Find the final angular velocity of the system.
Conservation of energy? Not because it is an inelastic collision (energy is not conserved).
Conservation of angular momentum!
mvr = Iω
0.05 x 300 x 0.2 = (½MR² + Md2) x ω
3 = (0.5 x 2 x 0.22 + 0.05 x 0.22) x ω
ω = 3 / 0.042 = 71.43 rad/s
500
Draw force arrows for this diagram. What forces are acting where?
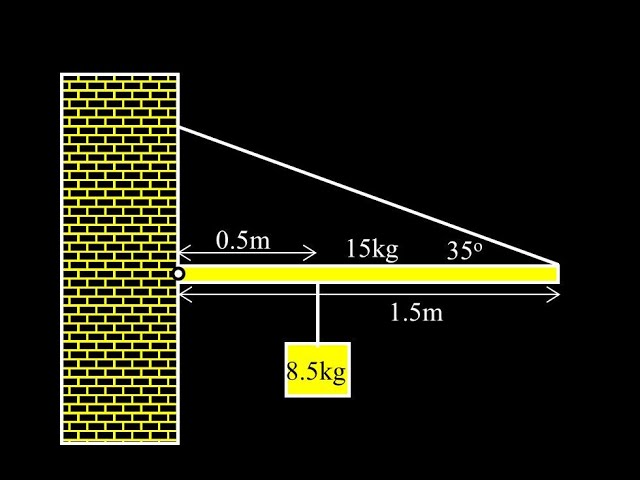
1. Hinge force (up / right)
2. Weight of beam in the middle (down)
3. Weight of 8.5 kg mass (down)
4. Tension (up / left)
500
A wheel is spinning at 10 rad/s and slows down with constant angular acceleration. After 8 seconds, it stops. How many radians did it rotate through before stopping?
ω₀ = 10 rad/s, ω = 0, t = 8 s
The average angular velocity is (ω₀ + ω)/2
θ = average angular velocity x t = ½(ω₀ + ω)t
½(10 + 0)(8) = 40 rad
500
A solid cylinder (I = ½MR²) and a hoop (I = MR²) roll down a ramp. Which reaches the bottom first and why?
Cylinder.
Energy is conserved within a closed system (always)! In rotational dynamics, energy (potential gravitational here) is converted to both translational and rotational kinetic energy. Since rotational kinetic energy is defined by KEr = ½ Iω², you know that there is more energy going to rotational motion for the hoop (bigger I) than the cylinder. Therefore, the cylinder reaches the bottom first.
500
A uniform rod that is 2 meters long and 3 kg is pivoted at one end and released from rest horizontally. What is the rod's angular speed just before hitting vertical?
Conservation of energy
mgh = KEr
mgh = 3g(1) --> 1 meter high because the center of mass is in the middle, and when it hits vertical position, it is exactly 1 meter from the "ground"
3g = ½ Iω²
30 = 0.5 x (1/3 ML2) x ω²
ω² = 30 / (0.5 x 1/3 x3 x 4)
ω = sqrt(15)
500
A solid cube and a solid sphere rolls down the ramp, which one hits the ground first?
The solid cube because it has not rotational motion, so all energy goes into linear translation.