List the area formulas for ALL THREE: rectangle, triangle, and parallelogram.
Rectangle: A=lw or A=bh
Triangle: A=bh/2
Parallelogram: A=bh
Find the volume of a rectangular prism with a Length of 3in, a width of 2in, and a height of 1in.
6 inches cubed
What is surface area?
the area of the surface of a 3-d shape
What is the difference between area and perimeter?
Area is the space that covers the surface of a shape and perimeter is the distance around a shape
Find the area of the triangle:
126 cm squared
Find the volume of a rectangular prism with a length of 4.67 in, a width of 12.4 in, and a height of 7.2 in. Round to the nearest hundredth.
416.94 in cubed
Find the composite area:
72 units squared
What is the formula for volume?
V= L x W x H
or
V= Area of the base x height
Find the area of the parallelogram:
72 cm squared
Find the volume:
1 7/9 cm cubed
Find the composite area of the shape:
50 yards squared
List 4 examples of 3-D shapes.
cube, rectangular prism, triangular prism, square pyramid, triangular pyramid, etc.
What is the area of the parallelogram?
76.5 feet squared
Find the volume of a rectangular prism with a length of 1/3 in, a width of 2/3 in, and a height of 1 1/2 in.
1/3 inches cubed
Find the Surface Area:
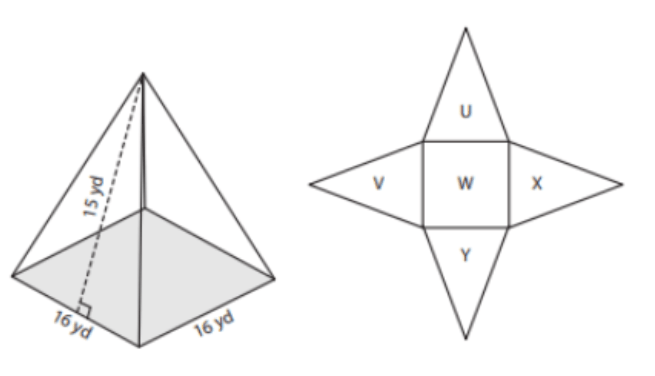
736 yards squared
List the steps for finding area of a composite shape.
1. Decompose/cut the shape into smaller shapes
2. Find the individual areas of each shape
3. Add the areas together to find the total area
The base of the triangle is 15 cm less than the height of the triangle. What is the area of the triangle?
792 cm squared
Find the volume of a rectangular prism with a length of 2 1/2 cm, a width of 1/3 cm, and a height of 3 cm.
2 1/2 cm cubed
Find the surface area:
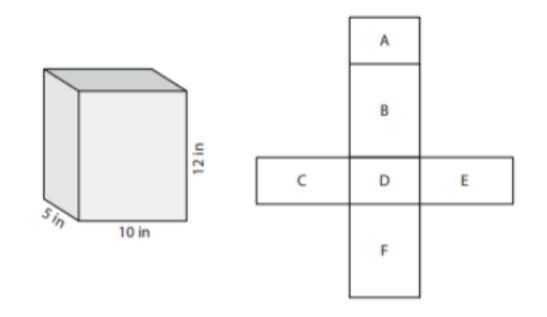
460 inches squared
Give a real world example of when we would need to find surface area and when we would need to find volume. (ex. the plastic on a water bottle vs. the water that is inside the water bottle)
multiple different answers