Radians
Unit Circle
Solving Linear equations
Finding arc lengths
Finding sector area
100
What is
(5pi)/6
equal in degrees?
150
100
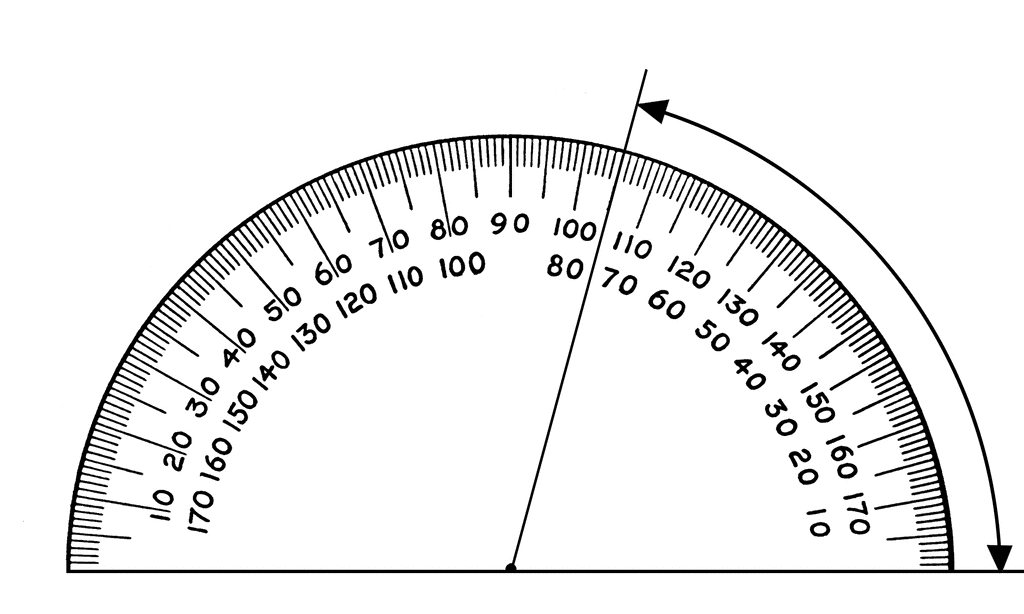
Plot an estimate of 75 degrees on the unit circle. Describe vicinity angles, such as 45 degreee in between 40 and 50, and it lies in quadrant 1, less than 90 degrees.
100
Solve for x when
x-25 = (x-36)/2
14
100
Find the arc length of a circle with a radius of 3 cm subtended by an angle of 30 degrees. (in radians)
pi/2
100
Find the area of the sector formed by a central angle of 1.4 radians in a circle of radius 2.1 meters
3.1m2
200
What is
361^. + 359^.
equal in radians?
4pi
200
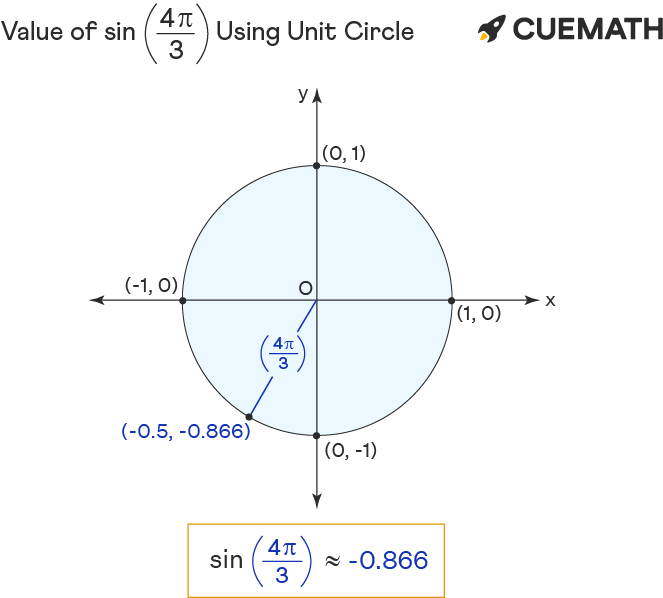
Plot an estimate of
(4pi)/3
on the unit circle. Describe vicinity angles, such as pi/4 in between pi/3 and pi/6, and it lies in quadrant 1, less than pi/2.
200
Solve for k,
k + 4pi=(100pi+8k)/10
30pi
200
Find the length of the sector (dark area)
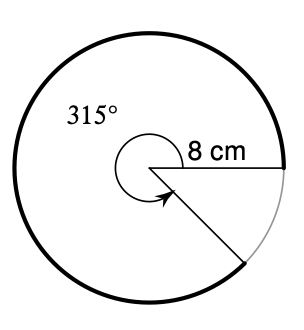
14pi cm
200
Find the area of the sector.
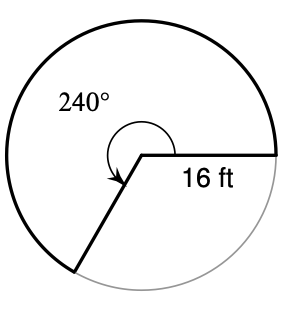
(512pi)/3 cm^2
300
What are the coterminal angles of
50^.
in radians? (between
3pi
and -2pi
(41pi)/18 and (-31pi)/18
300
Based on the unit circle, what are the terminal points of (3pi)/2 .
(0, -1)
300
solve for v,
(2v-45)/4 = (4v-5)/2
-35/6
300
If the diameter of a circle is 18 m and the central angle
(pi)/3
, find arc length substanded by to two decimal places.
9.42 m
300
If the sector formed by a central angle of 15. has an area of
pi/3
cm2, find the radius of a circle.
2sqrt2 cm
400
Convert to
175^.
to radians and hence find its reference angle in radians.
pi/36
400
Find the reference angle of
(13pi)/6
and hence draw the terminal side on the unit circle.
30 degrees or
pi/6
400
solve for
theta, theta+360^.=(2theta-5pi)/5
(5pi)/3
400
The pendulum of a clock is 36 cm long. If it swings through an angle of 21 degrees find the total distance travelled in one complete swing to one decimal place
26.4 cm
400
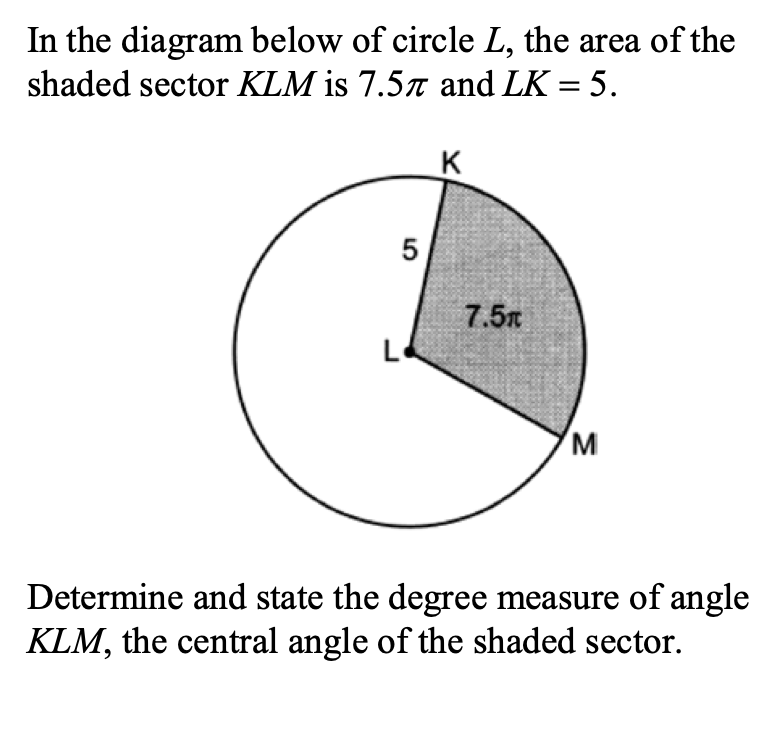
108 degrees
500
What are the coterminal angles and reference angles of 275 degrees in radians?
Reference angle =
(17pi)/36
Coterminal angles =
(127pi)/36 and (-17pi)/36
500
Draw the terminal side of 1140 degrees and hence find the reference angle and coterminal angles(between
2pi and 5pi
) of it in radians.
Reference angle =
pi/3
(multiple answers possible) Coterminal angle =
(7pi)/3 and (13pi/3)
500
Solve for m,
(30m+35pi)/(5pi) = (40m+8pi)/(3pi) +2
(49pi)/-2
500
An arc length of 1 ft is formed by a radius of 12 ft. Find the central angle in both radians and degrees.
In radians = 1/12
In degrees =
15/pi or 4.77^.
500
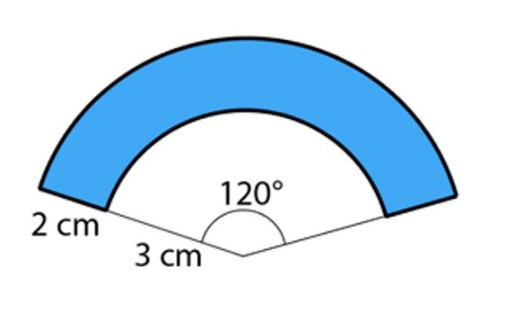Find the area of the shaded region
(8pi)/3