What is the value of 7:
17 084 641
7 000 000
What are the first 4 multiples of 6?
6, 12, 18, 24
Write 2 numbers from 1 to 10 that are PRIME.
2, 3, 5, and 7
12+3×5−8
19
A store had 350 apples. They sold 175 apples in the morning and 120 apples in the afternoon. How many apples are left in the store?
55
Write a number that is 10 000 more than 2 984 095
2 994 095
Find the first common multiple of 4 and 5.
20
What is the definition of a prime number?
Prime number is a number with exactly two factors. 1 and the number itself.
36÷(12−3×2)
6
A school is organizing a field trip. There are 12 classes going, and each class has 28 students. How many students are going on the field trip in total?
336 students
Write this number in standard form:
Eight billion nine hundred three million seven thousand nineteen
8 903 007 019
Find the first 3 common multiples of 3 and 6.
6, 12, 23
List all the factors of 33. Is 33 prime or composite?
Factors: 1, 3, 11, and 33.
33 is composite.
15−(7+3)÷2
10
Divide 49686 ÷ 12
4140 R 6
How many days will it take you to spend $1000 000 if you spend $100 each day?
10 000 days
Elys goes to the gym every two days and jogs every three days. Suppose she goes to the gym and jogs on March 1st. What is the next date on which she will jog and go to the gym?
March 7th.
Sofia and Helena are playing a game with this spinner. Sofia gets a point if the pointer lands on a prime number. Helena gets a point if the pointer lands on a composite number. Is this game fair? explain. 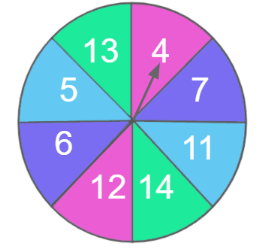
Yes. The game is fair because there are 4 prime and 4 composite numbers.
4 × 6 + (12 + 6) - 56 ÷7
34
A group of 14 students raised $11956. If they split the money equally, how much did each student get?
$854
How many days is 1 million minutes?
1 day = 24 hours x 60 min = 1440 min
1000 000 ÷ 1440 min = 694
About 694 days
Sarah is making party favor bags. She has 24 small candies and 18 mini chocolates. She wants to put the same number of candies in each bag and the same number of chocolates in each bag. What is the largest number of bags she can make so that she uses all the candies and all the chocolates? How many candies and chocolates in each bag?
6 bags with 4 small candies and 3 mini chocolates.
A classroom is organizing a game. They need to create two teams: a "Prime Team" and a "Composite Team."
- The "Prime Team" will consist of a number of students equal to a prime number between 5 and 15.
- The "Composite Team" will consist of a number of students equal to a composite number between 15 and 25.
- The total number of students in both teams combined must be a multiple of 5.
How many students could be on each team?
Possible Answers:
- 7 students on the "Prime Team" and 18 students on the "Composite Team."
- 11 students on the "Prime Team" and 24 students on the "Composite Team."
- 13 students on the “Prime Team” and 22 students on the “Composite Team.”
24 ÷ 6 + (4 × 8) × 3 + 4
104
A theatre has 7875 seats arranged in 75 rows. How many seats are there in each row?
105