Congruence
Similarity
Properties of triangles
Properties of parallelograms
Miscellaneous
100
What are congruent shapes?
Shapes that are the same size and same shape
100
What are similar shapes?
Shapes that are proportional to each other
100
How many degrees in a triangle?
180 degrees
100
How many degrees in a parallelogram?
360 degrees
100
How many degrees in a right angle?
90 degrees
200
SAS- Side Angle Side
200
Which rule determines similarity but not congruence?
AAA (Angle, Angle, Angle)
200
True or false. In isosceles triangles, two angles are equal in magnitude?
True
200
What is the defining feature of parallelograms?
Quadrilateral with both pairs of opposite sides parallel
200
Define bisect.
Crosses through the half way point
300
What is the first step to proving congruence?
Drawing a statement and reason table
300
Are all shapes that are similar also congruent?
No
300
What is the definition of an isosceles triangle?
Two sides the same length
300
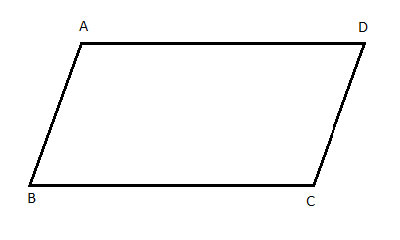In this parallelogram, which angles are equal?
Angle BAD = Angle ADC
Angle CBA = Angle BAD
Angle BAC = Angle BCD
Angle BAD = Angle CDA
Angle BAC = Angle BCD
300
Define the Z rule.
The internal angles made by two parallel lines and a third line which intersects both are equal in magnitude.
400
What is the minimum amount of information required to prove congruence?
Two angles and a side
Two sides and an included angle
Three sides
400
What is the minimum amount of information required to prove similarity?
Two sets of angles
400
If a property of an isosceles triangle is that two sides are the same, what is another property of an isosceles triangle?
Two angles are equal in magnitude
400
Which of these is not a parallelogram?
A)
B)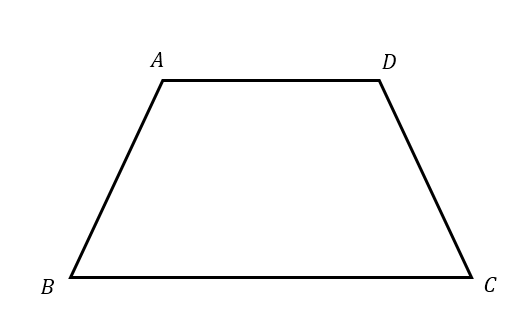
C)
D)
B - Trapezium
400
Vertically opposed angles is what rule?
X Rule
500
Write the steps to prove congruence in the following question.
In the quadrilateral ABCD, AB=AD, and AC is the angle bisector of BAD. Prove triangle ABC is congruent to triangle ADC.
AB = AD (given)
Angle BAC = Angle DAC (definition of bisect)
AC=AC (Same length)
Triangle ABC = Triangle ADC (SAS)
500
If these two triangles are similar, calculate the value of x.
x=15