Bivariate Data
Two-way tables
Time Series
Sequences
Earth Geometry and Time zones
100
Consider the following graph. Describe the linear association in terms of direction and strength.
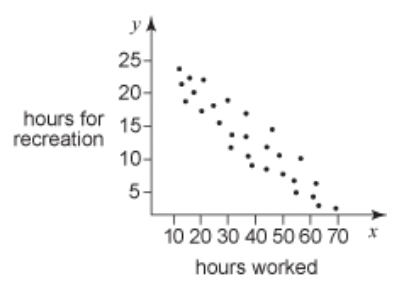
Negative, moderate, linear
100
survey was conducted with 242 university students. For this survey, data were collected on the students’ enrolment status (full-time, part-time) and whether or not each drinks alcohol (‘Yes’ or ‘No’). Their responses are summarised in the table below.
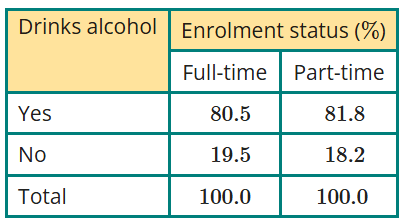
Is there an association between drinking alcohol and enrolment status?
No. The percentage of full-time and part-time students who drank alcohol is similar: 80.5% to 81.8%. This indicates that drinking behaviour is not related to enrolment status.
100
Three of the quarterly seasonal indices for a sales company are given in the following table.
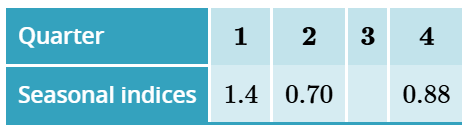
a) Calculate the seasonal index for the third quarter.
b) Interpret the value of the seasonal index for quarter 2.
a) 1.02
b) Quarter 2 = 0.70. This means that the sales for the second quarter are 30% below the average quarterly sales for the year.
100
In an arithmetic sequence, t_1=27 and d=-3
a) use the rule t_n=t_1+(n-1)d to model the sequence in simplified form.
b) Calculate t_15
a)
t_n=30-3n
b) -15
100
Determine the shortest distance between City X (15°N, 70°45’W) and City Y (15°N, 30°15’E).
10848.51 km
200
The equation used to predict the height (cm) of a child, in years, is:
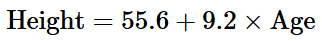
a) What is the rate at which a child is predicted to grow?
b) What is the height of a child predicted to be at birth?
a) The child is predicted to grow 9.2cm per year.
b) The child is predicted to have a height of 55.6cm at birth.
200
It has been suggested that females might be more satisfied with their lives overall than males. Data was collected from a sample of 360 adults and are summarised in the two-way frequency table below.
Calculate the percentage of respondents who are Female and satisfied with their life overall.
42.5% of the respondents were female and satisfied with their life overall.
153/360
200
The following set of data gives the number of houses sold by auction over a 12-month period for a real estate business.
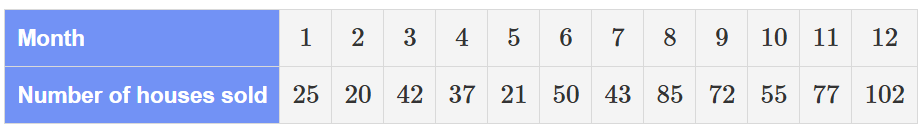
Calculate the three-mean smoothed value for August (month 8).
66.67
or 67
200
A geometric sequence is defined by the recurrence relation:
t_1=8, t_(n+1) =1.5t_n
a) determine the common ratio.
b) Write down the first 4 terms.
a) 1.5
b) 8, 12, 18, 27
200
Determine the shortest distance between city X (25°S, 162°E) and city Y (48°S, 162°E).
2557.6 km
300
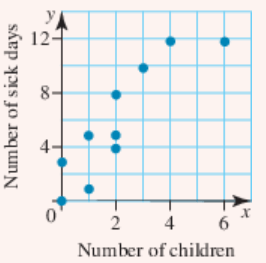
The following table shows the number of sick days taken by ten employees and relates this to the number of children that they have.
Create a scatterplot to display this data.
300
The following two-way frequency table shows the composition of left- and right-handed students in Years 11 and 12 at a school.
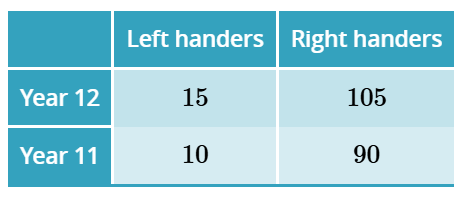
Calculate the percentage of all left-handers who are in Year 11.
40%
300
The seasonal index is 0.85 and the actual sales figure for a particular month is $102 000.
Calculate the deseasonalised figure.
$120,000
300
Jimmy bought a laptop for $2250. Given the rule to model the value of the laptop after n years is
V_n=2250xx0.95^n
a) determine the annual depreciation rate
b) determine the value of the laptop after 3 years
a) 5%
b) $1929.09
300
Tokyo is 135°E and Rio de Janeiro is 45°W. Determine the time difference between Tokyo and Rio de Janeiro.
Tokyo is 12 hours ahead of Rio de Janeiro
400
A golf club recorded the average weekly temperature and the number of cold drinks sold per week to determine how often they should send the golf cart with cold drinks around the course.
The data is shown in the table below:
a) use your calculator to determine the correlation coefficient ( r ) for the dataset given
b) describe the linear association in term of direction and strength
a) 0.76
b) positive, strong, linear
400
A number of people were surveyed and had their hair and eye colour recorded.
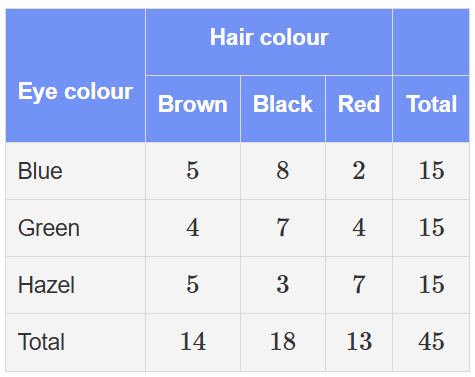
Of the people who had their hair colour recorded as red, calculate the percentage who also had an eye colour of green.
30.77%
400
A record of the maximum temperature recorded at the Richmond post office on 31 December for 8 years is recorded in the following table.
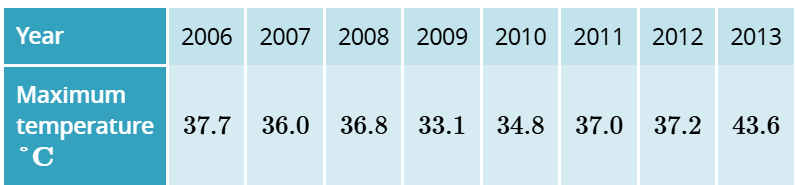
a) Determine the equation of the least squares line to fit the data.
b) Interpret the slope and y-intercept of the least squares line.
a)
y=-1149.54+0.59x
b) the B value of 0.59 is the slope. This means that for each increasing year, the temperate is predicted to increase by 0.59 degrees.
the A value of -1149.54 means that at the year 0, the temperature was predicted to be 1149.54 degrees below zero. This temperature is unlikely, and the discrepancy in predicted values may be due to this data is extrapolated from so far outside the range of the data collected.
400
The actual price of a 10-year-old car is $18,000. Calculate the residual when its price is predicted using the regression equation:
Price=35000−1500× Age
Predicted price = $20 000
Residual = -2000
This means that the actual value of the car is $2000 less than the predicted value.
400
Determine the day and time in London (UTC +0) when it is 15:00 on Friday in Tokyo (UTC +9).
The time in London is 6:00 am on the same day (Friday).
500
The following table shows weight and height for a group of men and women.
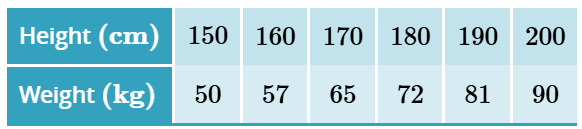
a) Use your calculator to determine the correlation coefficient ( r ) for the dataset given.
b) Describe the linear association in terms of direction and strength.
c) Use a calculator to determine the equation of the least squares line to fit the data.
a) 0.9987
b) Positive, Strong
c)
y=-70.33+0.7971x
500
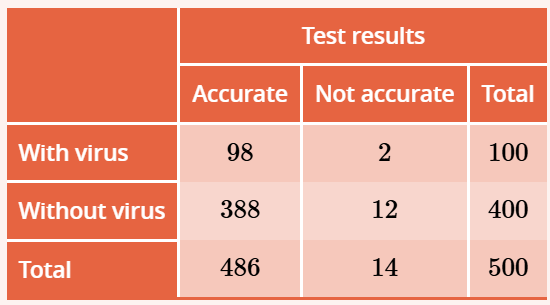
A test is developed to test for infection with the flu virus. To test the accuracy, the following 500 people are tested.
Of the 100 people who are known to have the flu who are tested, the test returns 98 positive results.
Of the 400 people who are known not to be infected with the virus who are tested, 12 false positives are returned.
Display this information in the following two-way frequency table.
500
The mortality rate from a particular type of cancer following the discovery of a new drug is shown in the following table.
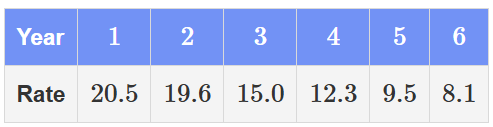
Calculate the centred 4-point moving average for year 3, correct to 2 decimal places.
15.48
500
The batteries in a toy robot are running down. The toy robot marches 50cm in the first minute, 30 cm in the second minute, 18 cm in the next and so on.
Determine the total distance the toy robot has marched in the first 8 minutes? (Answer correct to 2 decimal places.)
The toy robot will march 122.90 cm in the first 8 minutes.
500
A plane is flying from Munich (48∘N,15∘W) to New York (41∘N,75∘W) . The flight departs Munich at 6.00 pm and takes 7 hours. Calculate the time of arrival in New York.
Angular difference =75∘ - 15∘
=60∘
Time difference =60÷15
=4h
New York is further west, and so is behind Munich. Plane leaves 6:00 pm Munich time. 4 hours before 6:00pm is 2:00pm. The plane leaves Munich at 2pm New York Time.
Flight takes 7 hours. 2 + 7 = 9 Therefore the plane arrives 9:00pm New York time (the same day).