What is size of x? Give reasons for how you know.
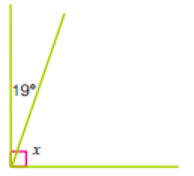
x = 71° (both angles make a right-angle which is equal to 90° OR the angles are complementary).
Find the size of angle c. Show your working.
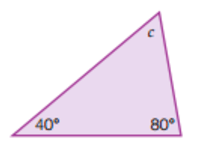
c = 180°- 40° - 60° (angles in a triangle add up to 180°)
c= 60°
Find the size of angle a. Give reasons for how you know.
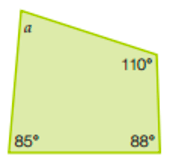
a = 360° - 110° - 85° - 88° (angles in a quad add up to 360°)
a = 77°
What is the size of angle x? Give reasons for how you know.
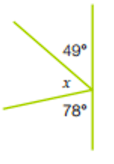
x = 180° - 49° - 78 ° (angles on str. line add up to 180°)
x = 53°
Give name of this triangle according to its angles and sides.
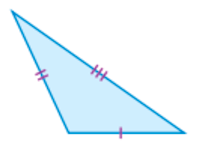
Obtuse scalene triangle
Calculate the size of angle x. Give reasons for how you know.
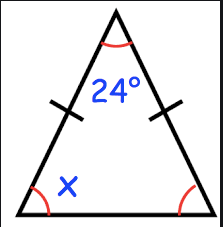
x = (180 ° - 24°)/2
Angles in a triangle add up to 180° and since the triangle is isosceles the base angles are equal.
x = 156/2=78°
What is the size of angle e? Give reasons for how you know.
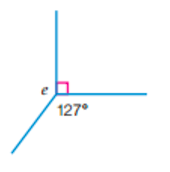
e = 360° - 90° - 127° (angles around a point add up to 360°)
e = 143°
What is the value of e? Give reasons for how you know.
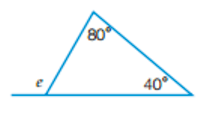
The missing angle in the triangle = 180° - 80° - 40° (angles in a triangle add up to 180°)
Missing angle = 60°
e = 180° -60° (angles on a str. line add up to 180°)
e = 120°
Find the size of angle c.
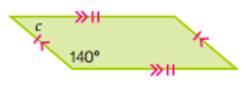
The angle opposite 140° is also 140° because opposite angles in a parallelogram are equal.
So then both of those angles are 140° + 140° = 280°
c = (360° - 280°)/2=40°
(angles inside a quad add up to 360°)
What is beta equal to? Give reasons for your answer.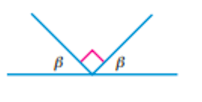
beta = (180°- 90°) /2
(angles on a str. line add up to 180°)
(90°)/2=45°
What is the value of b?
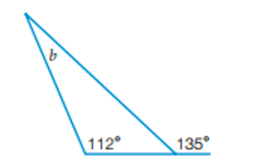
180° - 135° = 45° (angles on a str. line add up to 180°)
b = 180° - 112° - 45° = 23° (angles in a triangle add up to 180°)
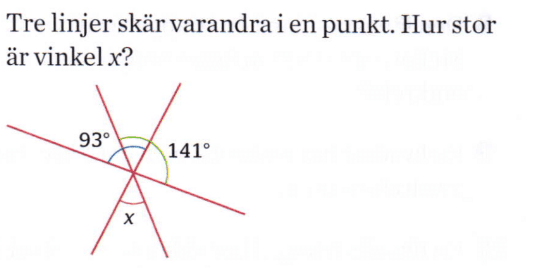
141° + 93° = 234° but angles on a straight line add up to 180°
So 234° - 180° = 54° which is the size of the overlap between the green and blue arc
x = 54° (vertically opposite angles are equal)
What is y equal to? Give reasons for your answer.
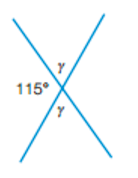
y = 180° - 115° (angles on a str. line add up to 180°)
y = 65°
The other y also equals 65° because vertically opposite angles are equal.
Find the angles for all the letters.
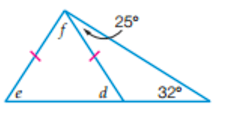
d = 57°
e = 57°
f = 66°
A quadrilateral has angles of 70°, 34° and two other unknown angles. One of the unknown angles is 55° bigger than the other one.
What is the value of the unknown angles?
360° - 70° - 34° = 256°
Both unknown angles add up to 256°
(256°)/2= 128°
256° - 55° = 201°
(201°)/2=100,5°
100,5° + 55° = 155,5°
The bigger unknown angle is 155,5° and the smaller unknown angle is 100,5°.