Algebraic Skills
Positives and negatives, solving equations
Geometric relationships
Triangles - angles, congruence
Combine Geometry and Algebra
100
Brian, Jenny and Sarah all collect footy cards.
Jenny has 6 more than Brian.
Sarah has triple the amount that Brian has.
If Brian has b cards, write expressions for the number of cards Jenny has, and the number of cards Sarah has.
Jenny has b + 6 cards
Sarah has 3b cards
100
Solve these addition and subtraction problems:
1. 6 + -10
2. -8 + -3
3. -4 - -9
Solutions:
1. -4
2. -11
3. 5
100
Find the missing angle in these two diagrams.
52 degrees
115 degrees
100
Will the three angles in this triangle add up to 90, 180 or 360 degrees?
Once you have worked this out, work out the size of angle x.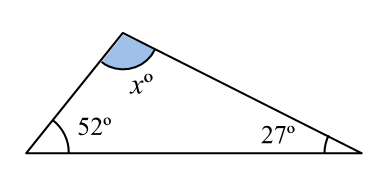
Angles in a triangle always add up to 180 degrees.
Angle x = 101 degrees.
100
1. By collecting like terms, write an expression for the sum of the two angles in this diagram.
2. Use the fact that the two angles in the diagram are complementary to construct an equation.
3. Solve the equation for g.
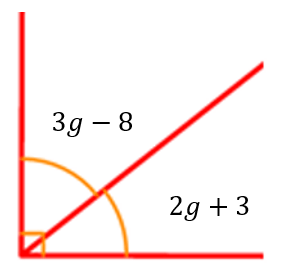
1. 3g - 8 + 2g + 3 = 5g - 5
2. 5g - 5 = 90
3. g = 19
200
Simplify these expressions by collecting like terms:
Expression 1: 5t - 3r - 8r + t
Expression 2: -7j - 9h + 3h + 10j
Expression 1: 6t - 11r
Expression 2: 3j - 6h
200
Solve these multiplication and division problems
1. 9 xx -4
2. (-18) / -6
3. -5 xx -3
1. -36
2. 3
3. 15
200
How large is the angle marked with an x?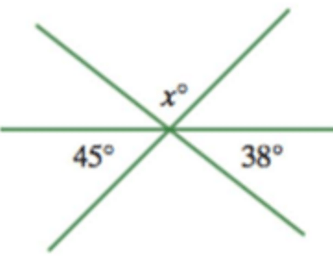
x = 97 degrees.
200
Both of these triangles have a missing angle, marked in blue.
Determine the size of each missing angle.
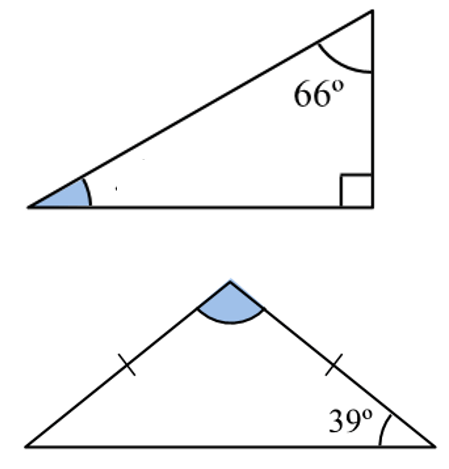
1. 24 degrees (remember the square in the corner represents a right angle, or 90 degrees)
2. 102 degrees (this is an isosceles triangle - two sides are the same, two angles are the same).
200
1. By collecting like terms, write an expression for the sum of the three angles in this triangle.
2. Use a known fact about the sum of three angles in a triangle to construct an equation.
3. Solve the equation for m.
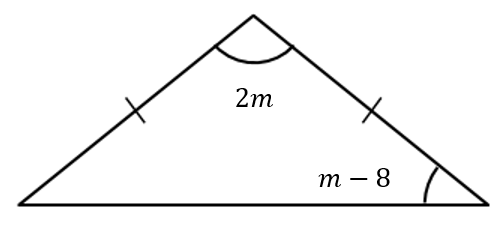
1. 2m + m - 8 + m - 8 = 4m - 16
2. 4m - 16 = 180
3. m = 49
300
Expand the brackets for these expressions:
Expression 1: 5(n - 4)
Expression 2: 4(3p + 2)
Expression 1: 5n - 20
Expression 2: 12p + 8
300
Solve these equations:
1. x-3=12
2. 3h-5=1
3. (p+6)/4=-2
1. x = 15
2. h = 2
3. p = -14
300
For each of angles x and y:
- state their relationship to the angle 57 degrees (are they CORRESPONDING, CO-INTERIOR, or ALTERNATE)?
- state the size of the angle
x is ALTERNATE to the 57 degree angle.
x = 57 degrees (alternate angles are the same size)
y is CO-INTERIOR with the 57 degree angle
y = 123 degrees (co-interior angles add up to 180)
300
Which two triangles are congruent, and why?
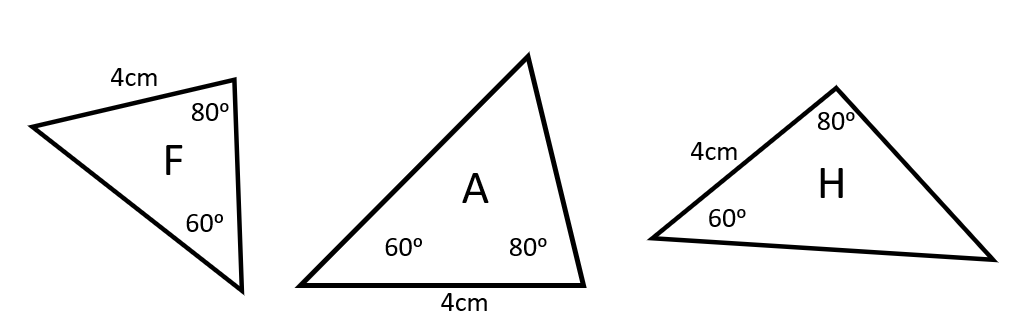
A and H are congruent using the ASA test (two angles that are the same, and one corresponding pair of sides).
300
1. What will be the sum of the angles marked 68 degrees and 5(d-2), and why?
2. Set up an equation and solve it for d.
3. Set up an equation and solve it for k.
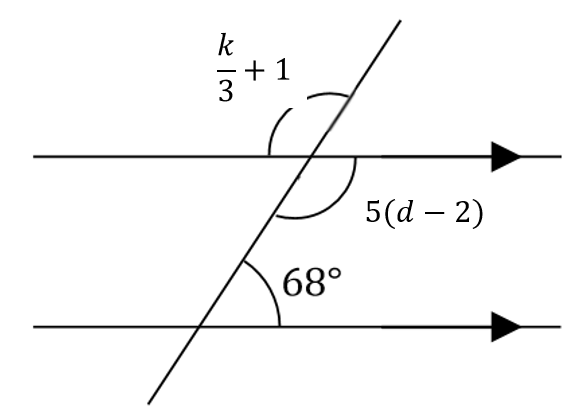
1. These two angles will add up to 180 degrees because they are CO-INTERIOR.
2. 5(d-2) + 68 = 180 or 5(d-2) = 112
d = 24.4
3.
k/3+1=112
k = 333
400
Factorise these algebraic expressions:
Expression 1: 6h - 24
Expression 2: 10j + 35
Expression 1: 6(h - 4)
Expression 2: 5(2j + 7)
400
Solve these equations:
1. 8(r-7)=34
2. 4y+9=-1
3. 5x-3=2x-21
1. r = 11.25
2. y = -2.5
3. x = -6
400
One of these angles is corresponding with the 119 degree angle - which one?
Then, determine the size of x, y and z.
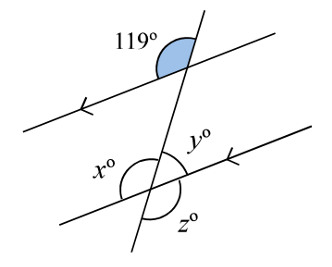
x is corresponding to 119.
x = 119 degrees (corresponding angles are the same size).
y = 61 degrees.
z = 119 degrees.
400
Which two triangles are congruent, and why?
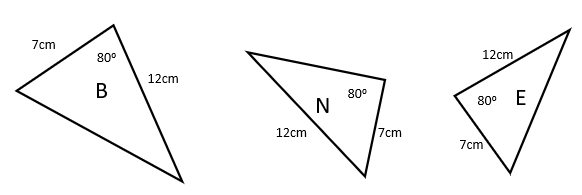
B and E are congruent using the SAS test (two pairs of sides are the same, and the angle between the sides are the same).
400
It is known that these two angles are congruent.
Find the value of x.
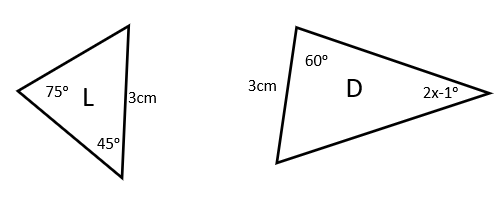
2x - 1 = 75
x = 38