Translation Of Shapes
Rotation Of Shapes
Reflection Of Shapes
Dilation Of Shapes
Diverse Questions
200
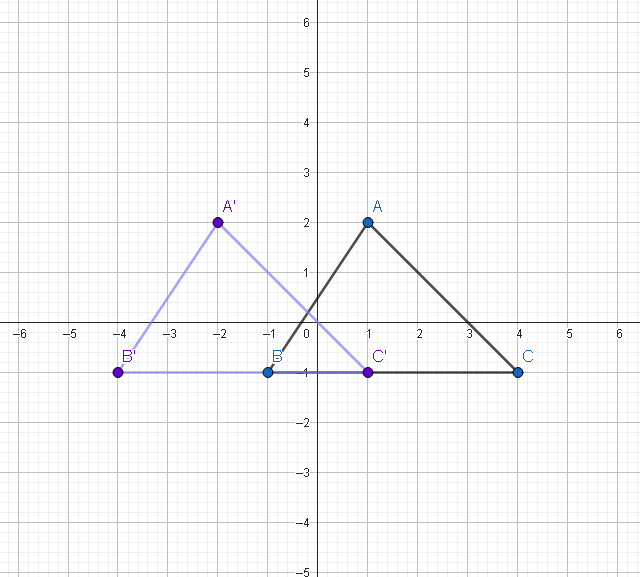
Draw the image of quadrilateral ABC under a translation by 3 units to the left.
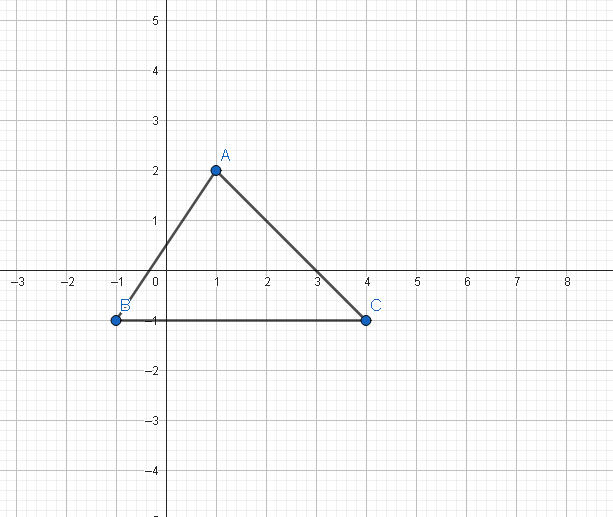
1. Translate quadrilateral ABC's vertices and connect them.
2. For example: point C(4,-1) is translated to
(1,-1)
200
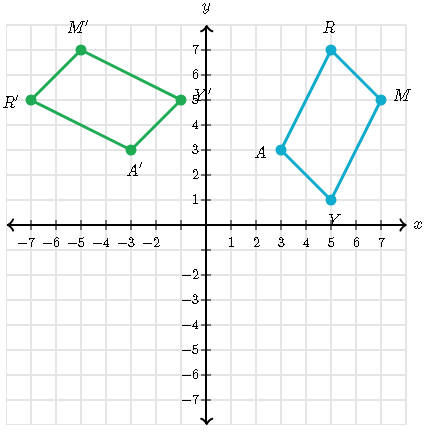
Quadrilateral ARMY is rotated 90° about the origin.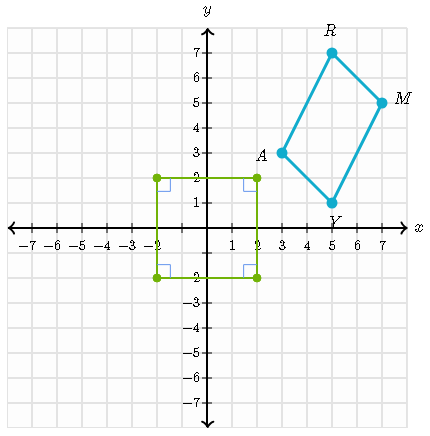
Rotating a figure 90 degrees about the origin, every point (a,b) on this figure maps into the point (-b,a)
For example: the point M(7,5) on quadliratel ARMY maps onto the point (-5,7).
Rule:
90=(a,b)to(-b,a)
200
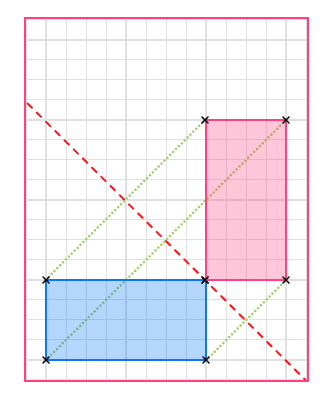
Reflect the shape in the line:
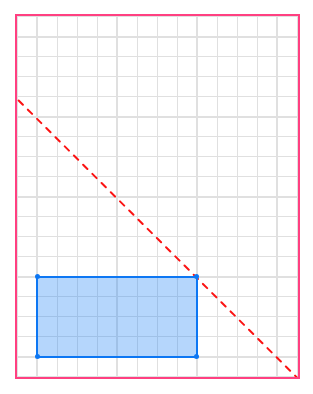
1. Reflect the first point because its the closest
2. Reflect the other points
200
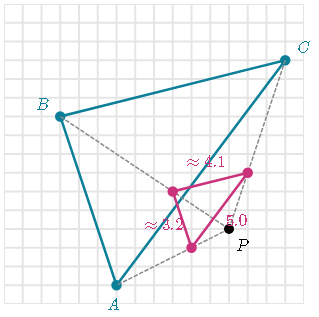
Draw the image of triangle ABC under a dilation whose center is P and the scale factor is 4
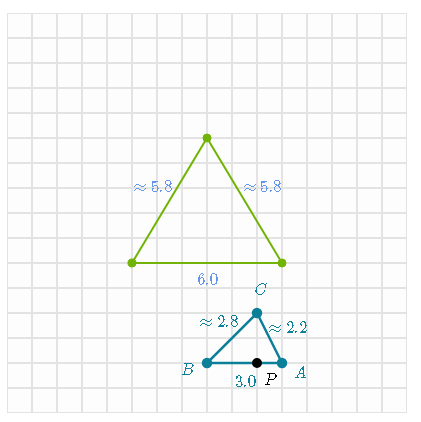
Dilate all of triangle ABC's vertices and connect them
For example: point B is 2 units to the left of P so its image 4 x 2 = 8 units to the left from P
200
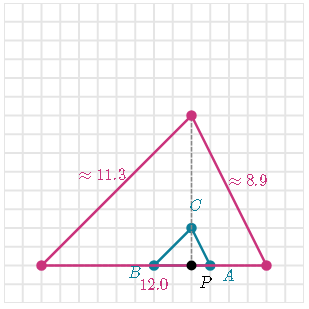
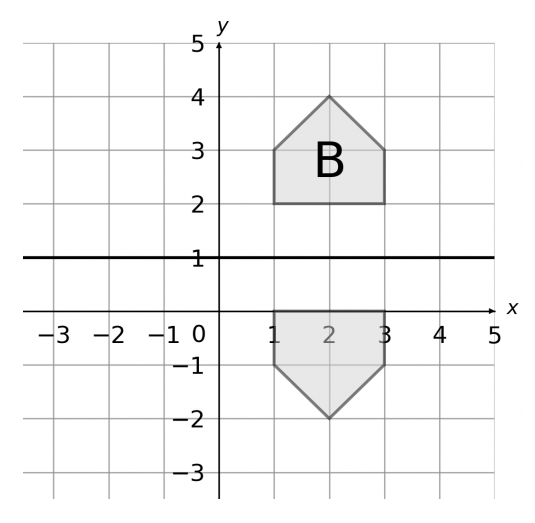
Reflect shape B in the line y=1
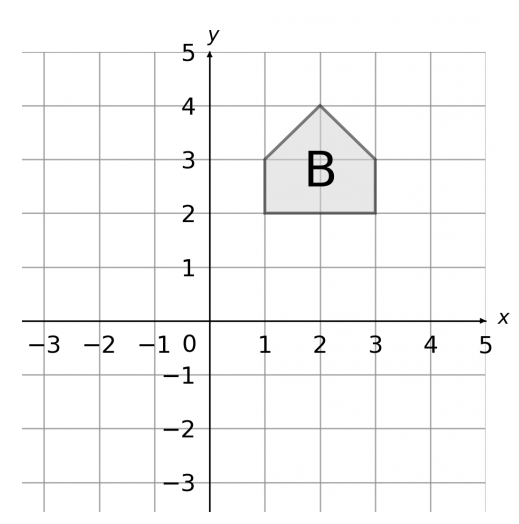
1. Draw the line y=1 onto the graph
2. the trace of the shape is the result of the reflection. Draw that shape onto the original axes
400
Draw the image of quadrilateral ABCD under a translation by 2 units to the left and 3 units up.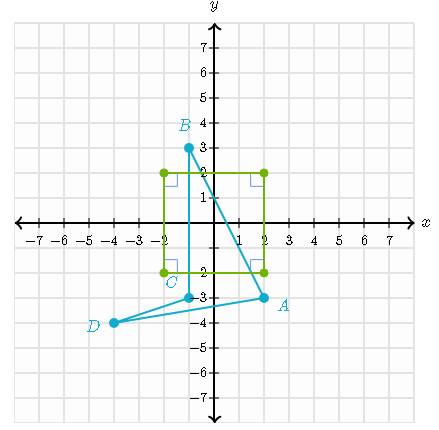
1. Translate quadrilateral ABCD's vertices and connect them.
2. For example: point C(-1,-3) is translated to
(-3,0)
400
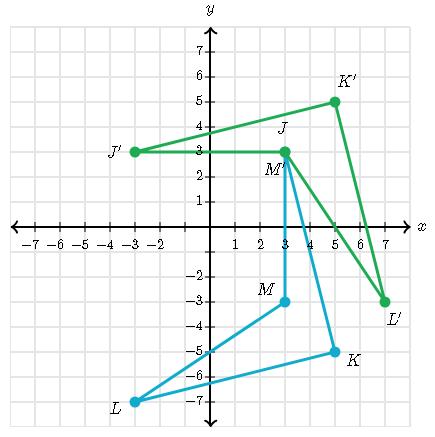
Quadrilateral JKLM is rotated -270° about the origin.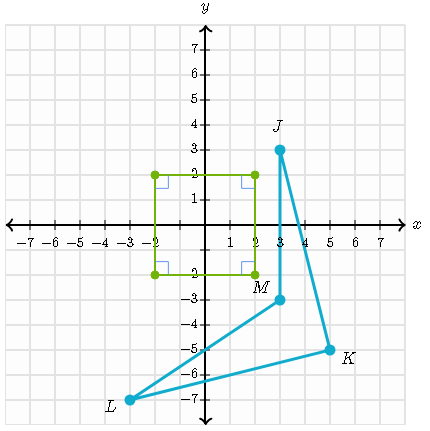
Rotating a figure -270° about the origin, every point (a,b) on this figure maps into the point (-b,a)
For example: the point M(3,-3) on quadliratel JKLM maps onto the point (3,3).
Rule:
-270°=(a,b)to(-b,a)
400
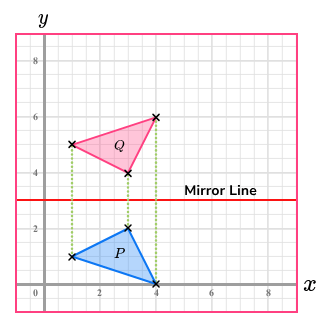
Reflect the triangle P in the line y=3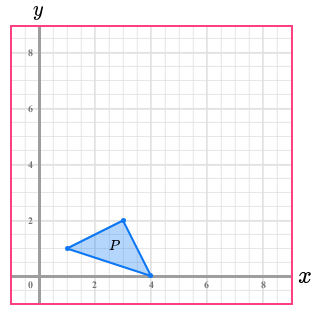
1. Draw the mirror line on y=3
2. Reflect the first point because its the closest
3. Reflect the other points
400
Draw the image of triangle ABC under a dilation whose center is P and the scale factor is 1/3
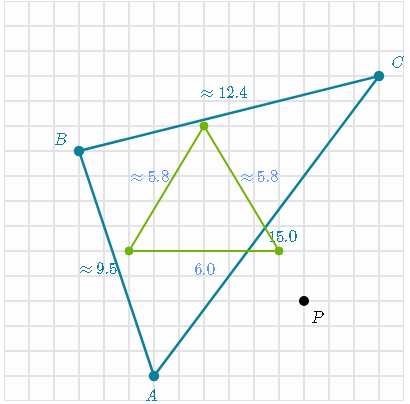
Dilate all of triangle ABC's vertices and connect them
For example: point C is 3 units to the right of P and 9 units up so its image 1/3 x 3 = 1 unit to the right and 1/3 x 9 = 3 units up from P
400
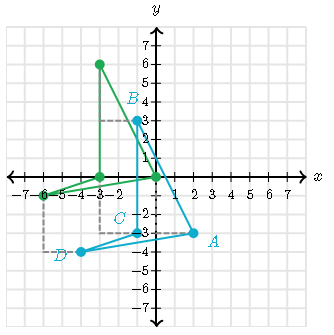
Describe fully the transformation that takes shape D onto shape E
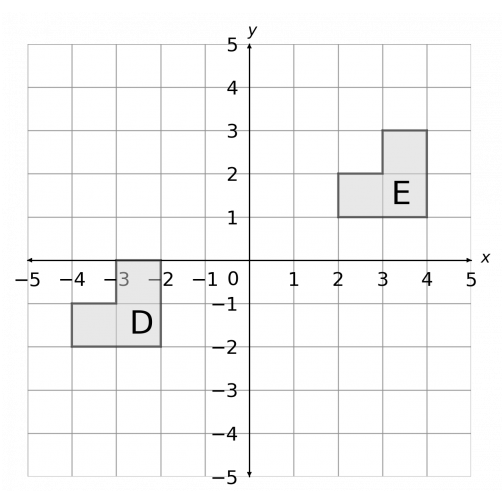
The two shapes look the same and have the same direction, so they don't rotate or reflect.
It has been shifted 6 spaces to the right and 3 spaces up
Translation by the vector:
(6/3)
600
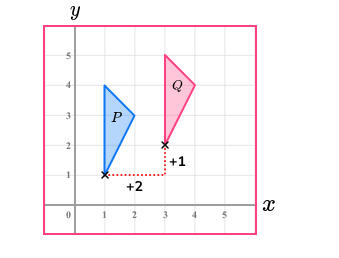
Describe the translation of shape P to shape Q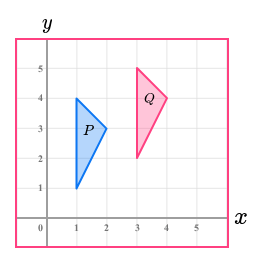
1. Work out the horizontal movement
2. Work out the vertical movement
3. State the column vector
Up=1
Right=2
(2/1)
600
Write a rule to describe the transformation.
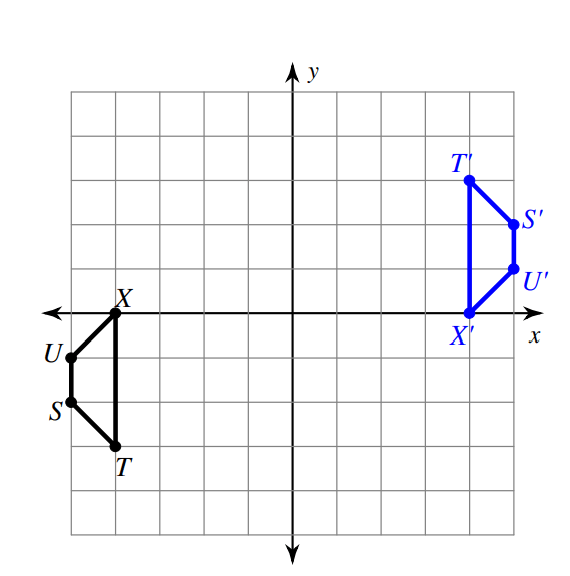
Rotating a figure 180° about the origin, every point (a,b) on this figure maps into the point (-a,-b)
For example: the point X(-4,0) on quadliratel TSUX maps onto the point (4,0).
Rule:
180°=(a,b)to(-a,-b)
Answer:
Rotation 180° about the origin.
600
Describe the transformation of Shape A to Shape B
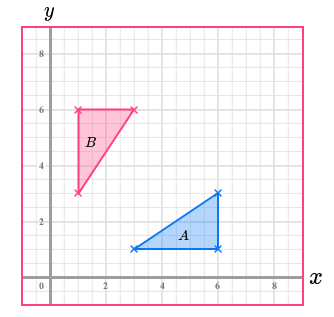
1. Pair up the points
2. Identify the midpoints
3. Join the midpoints
4. State the equation of the line
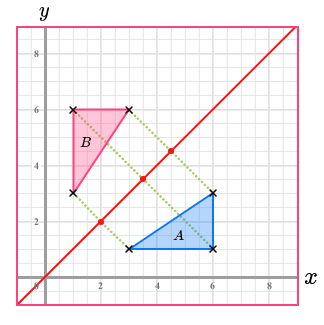
The equation of the line is:
y=x
600
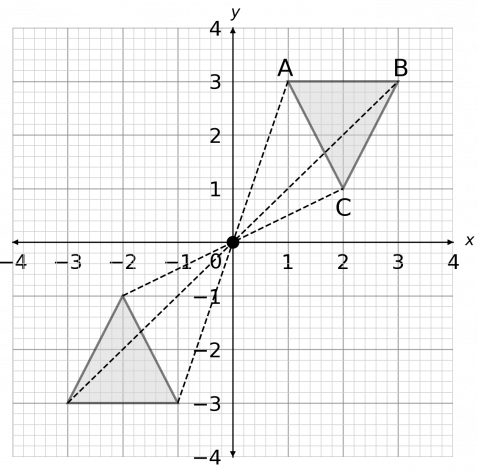
Enlarge shape ABC by scale factor -1 about the origin
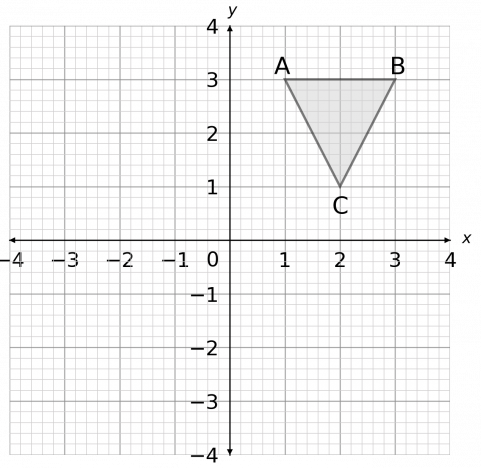
Because the scale factor is -1, the extension part of the lines (the part that goes outward from the origin, away from the shape) will be the same length as the original lines drawn from the corners to ABC.
For example: the line from the origin to C goes 2 to the right and 1 up. So, the extension to this line will, from the origin, go 2 to the left, and 1 down.
600
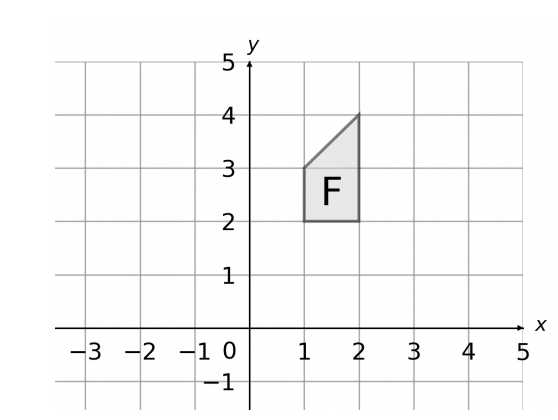
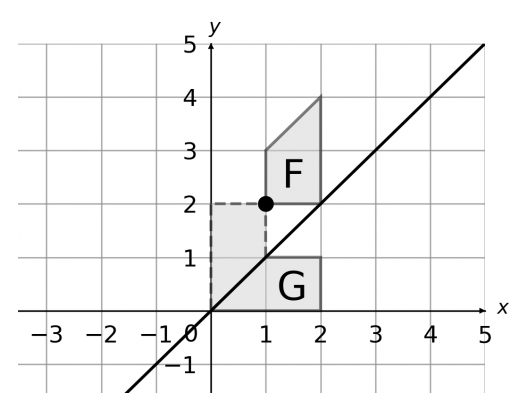
Perform the following transformations to shape F in the order given
1. Rotation 180° about (1,2)
2. Reflection in the line y=x
1. The new origin is (1,2), so the points:
(2, 4) becomes (0, 0)
(1, 3) becomes (1, 1)
(1, 2) remains (1, 2)
(2, 2) becomes (0, 2)
2. Reflect a point across the line y = x, the x-coordinate and y-coordinate change places.
(0, 0) remains (0, 0)
(1, 1) remains (1, 1)
(1, 2) becomes (2, 1)
(0, 2) becomes (2, 0)
800
Draw the image of triangle ABC under the translation (x,y)\to(x-6,y-7).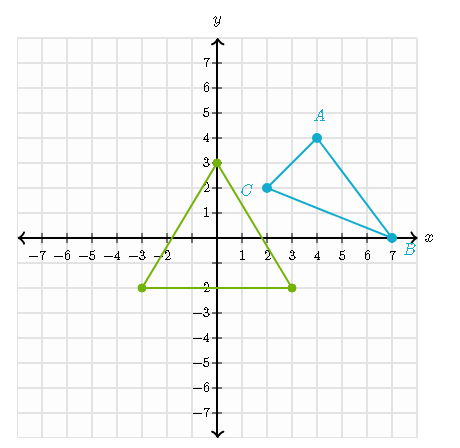 
1. Translate the triangle's vertices and connect them
2. For example: point A(4,4) is translated to
(4-6,4-7)=(-2,-3)
800
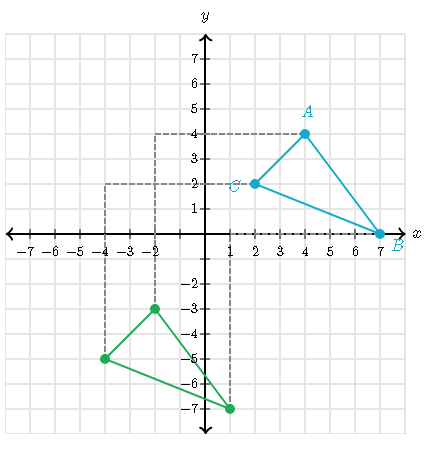
Rotate the following figure 180° about the point (-1,1).
The new origin is (-1,1), so the points will change into (-7,-1), (5,0), and (6,-5)
Rotating a figure 180° clockwise about the point (-1,1), every point (a,b) on this figure maps into the point (-a,-b)
For example: point (5, 0) maps onto the point (-5, 0).
to(7,1),(-5,0)and(-6,5)
Rule:
180°=(a,b)to(-a,-b)
800
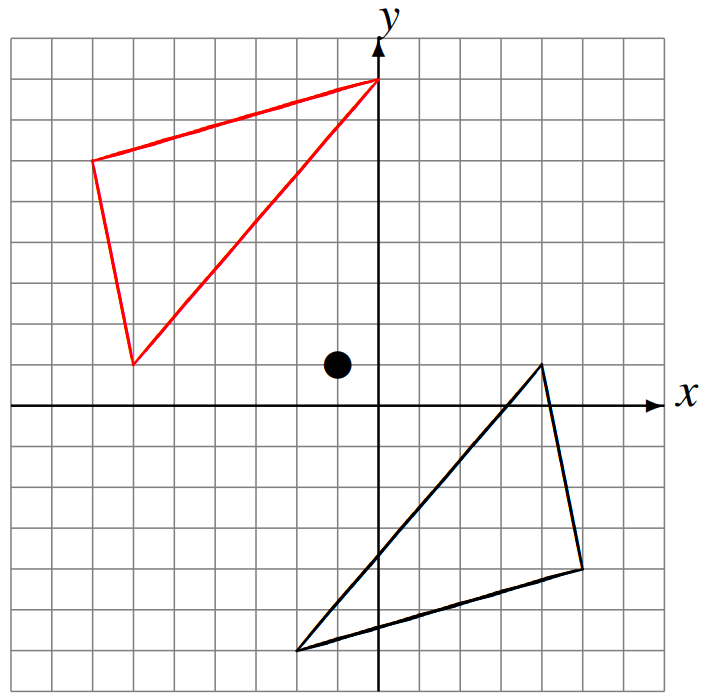
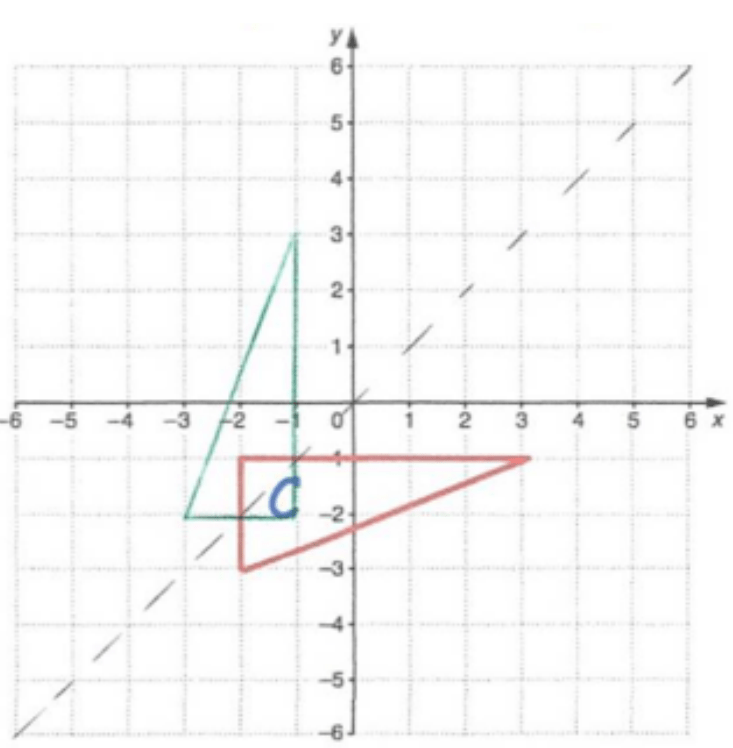
Reflect the triangle in the line y=x.
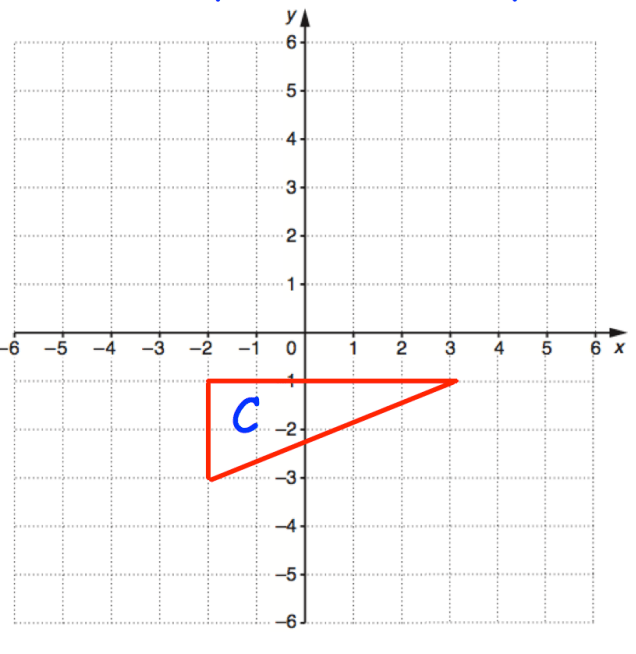
Reflecting a point across the line y = x, the x-coordinate and y-coordinate change places.
(3, -1) remains (-1, 3)
(-2, -1) remains (-1, -2)
(-2, -3) becomes (-3, -2)
800
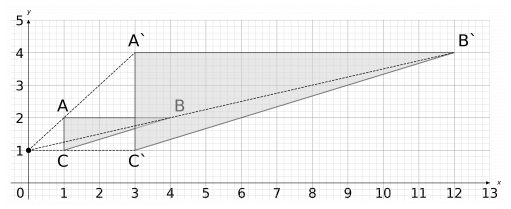
Enlarge shape ABC by scale factor 3 using (0,1) as the center of enlargement
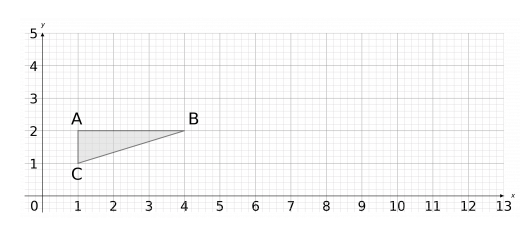
We need to draw lines from the point (0,1) to all corners of this shape. Then, since this is an enlargement of scale factor 3, we need to extend these lines until they are 3 times longer.
For example: the line from (0,1) to A goes 1 space to the right and 1 up. The resulting line should go 3 spaces to the right and 3 spaces up.
800
Reflection across y=x
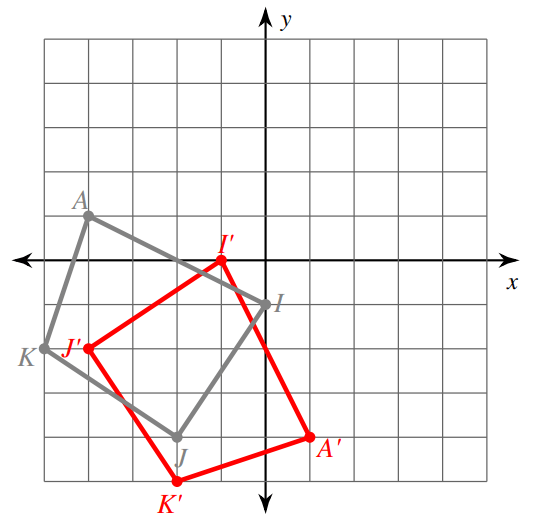
K(−5, −2)
A(−4, 1)
I(0, −1)
J(−2, −4)
1. Plot the points on the graph
2. Reflecting a point across the line y = x, the x-coordinate and y-coordinate change places.
K(-5, -2) becomes (-2, -5)
A(-4, -1) becomes (-1, -4)
I(0, -1) becomes (-1, 0)
J(-2, -4) becomes (-4, -2)
1000
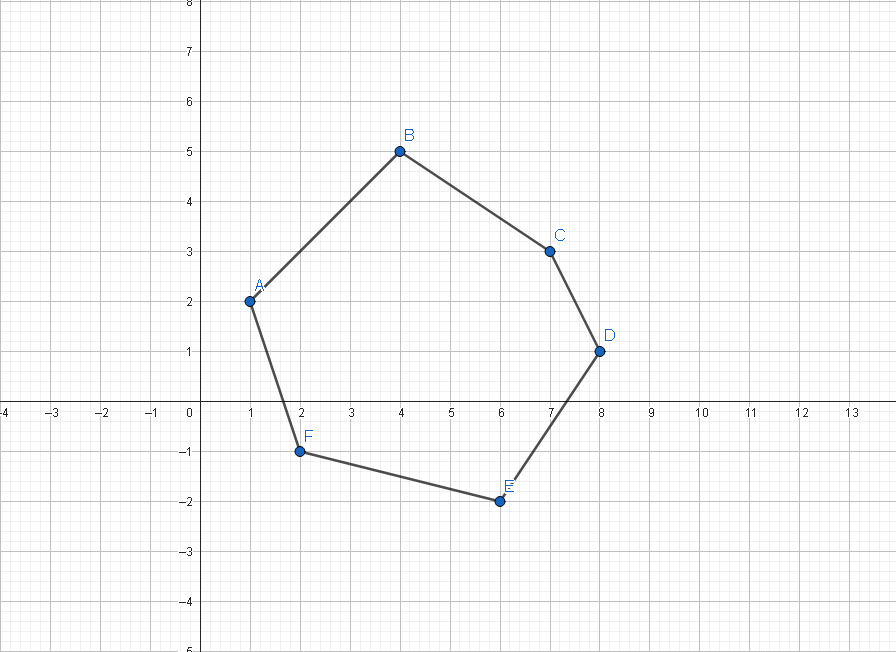
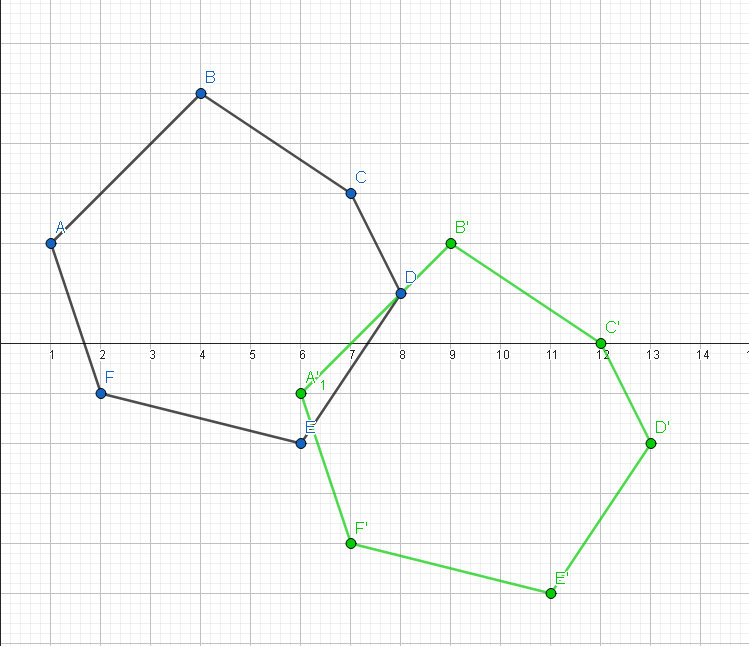
Given a hexagon with vertices A(1, 2), B(4, 5), C(7, 3), D(8, 1), E(6, -2), and F(2, -1), perform a translation by a vector (5, -3). Determine the new coordinates of each vertex after the translation.
Add 5 to the x-coordinate and subtract 3 from the y-coordinate for each vertex.
A' = (1 + 5, 2 - 3) = (6, -1)
B' = (4 + 5, 5 - 3) = (9, 2)
C' = (7 + 5, 3 - 3) = (12, 0)
D' = (8 + 5, 1 - 3) = (13, -2)
E' = (6 + 5, -2 - 3) = (11, -5)
F' = (2 + 5, -1 - 3) = (7, -4)
1000
Point Q was rotated by -150^\circ (the center of rotation is indicated)
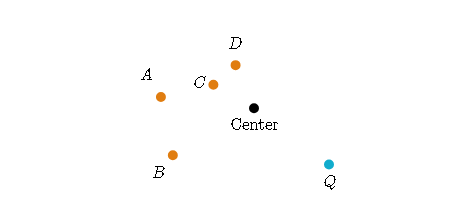
Imagine a circle that passes through point Q with the given center
find the point on that circle -150^\circ clockwise from point Q
A 150^\circ angle takes up 5/12 of the circle
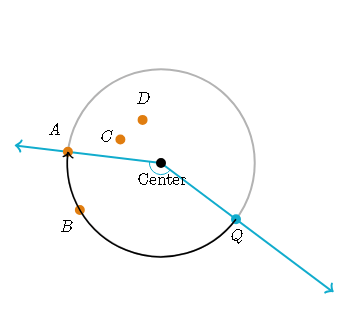
Point A is the image of point Q
1000
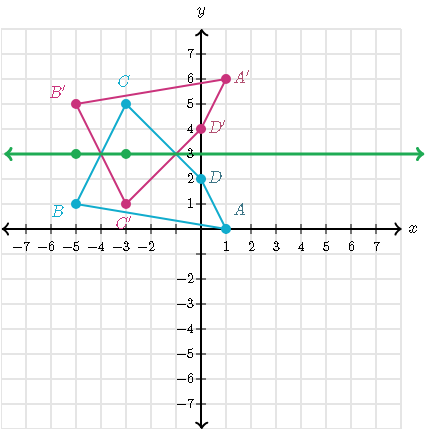
Draw the line of reflection that reflects quadrilateral ABCD onto quadrilateral A'B'C'D'
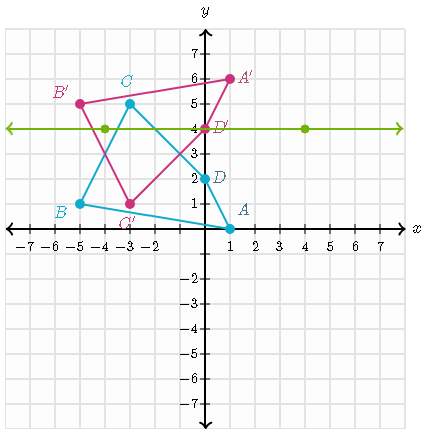
Find the midpoint between B(-5, 1) and B'(-5, 5)
x=-10/2=-5
y=6/2=3
The midpoint of B and B' is (−5,3)
We can find the midpoint of another pair of points. For example: the midpoint of C(-3, 5) and C'(-3, 1) is (-3, 3), so the line of reflection passes through (-5, 3) and (-3, 3)
The line y = 3 reflects quadrilateral ABCD onto quadrilateral A'B'C'D'
1000
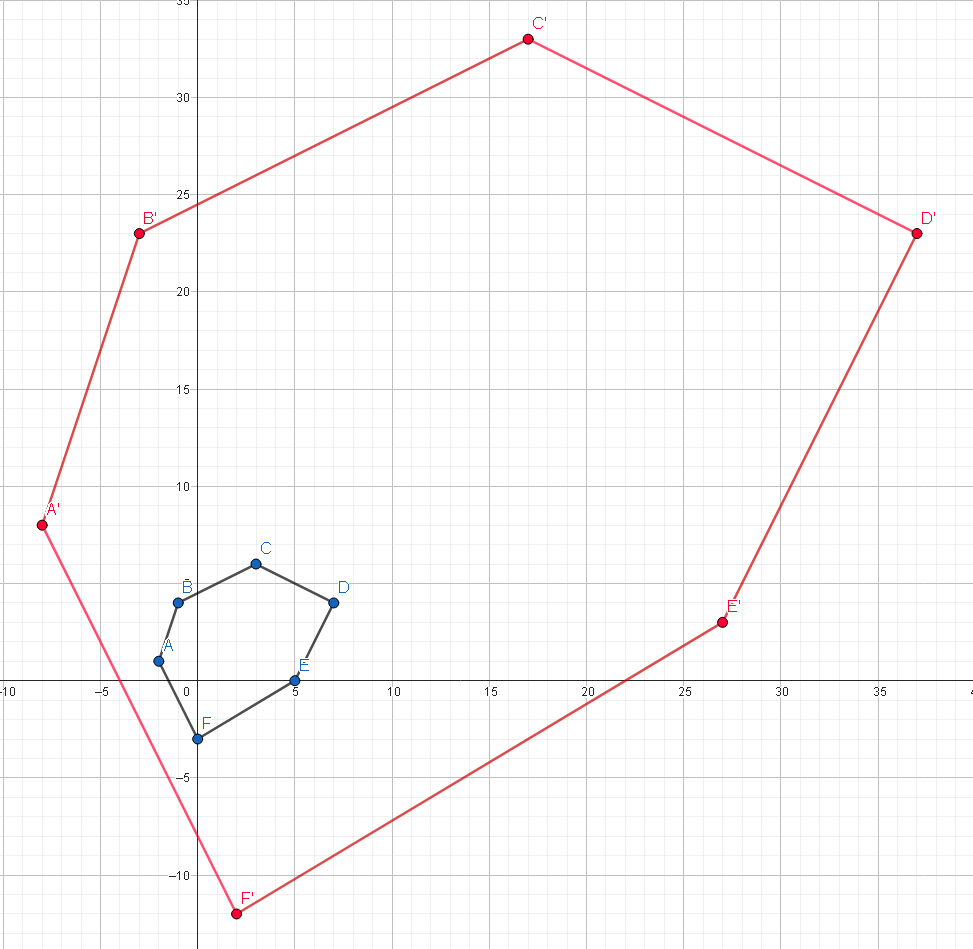
Consider a polygon with vertices at A(-2, 1), B(-1, 4), C(3, 6), D(7, 4), E(5, 0), and F(0, -3). Perform a dilation of this polygon with a scale factor of 5 centered at the point (2, 3). Calculate the new coordinates of each vertex after the dilation and plot the graph.
A(-2, 1):
( 2 + 5 ( − 2 ) , 3 + 5 ( 1 ) ) = ( − 8, 8 )
B(-1, 4):
( 2 + 5 ( − 1 ) , 3 + 5 ( 4 ) ) = ( − 3, 23 )
C(3, 6):
( 2 + 5 ( 3 ) , 3 + 5 ( 6 ) ) = ( 17, 33 )
D(7, 4):
( 2 + 5 ( 7 ) , 3 + 5 ( 4 ) ) = ( 37, 23 )
E(5, 0):
( 2 + 5 ( 5 ) , 3 + 5 ( 0 ) ) = ( 27, 3 )
F(0, - 3):
( 2 + 5 ( 0 ) , 3 + 5 ( - 3 ) ) = ( 2, - 12 )
1000
Quadrilateral A'B'C'D' is the image of quadrilateral A B C D under a dilation
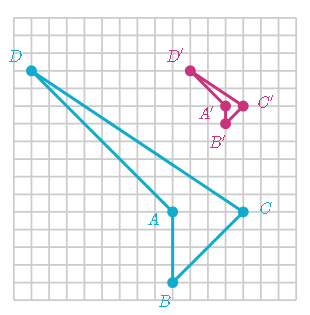
What is the scale factor of the dilation?
\frac{\text{length of image}}{\text{length of source}}=\text{scale factor}
Let's compare the lengths of \overline{AB} and \overline{A'B'}
frac{A'B'}{AB}=frac{1}{4}
The scale factor of the dilation is:
1/4