Solving Systems of Linear Inequalities
Exponents
Fractions
Solving Systems of Linear Equations
True or False
100
Write an inequality to match the graph.
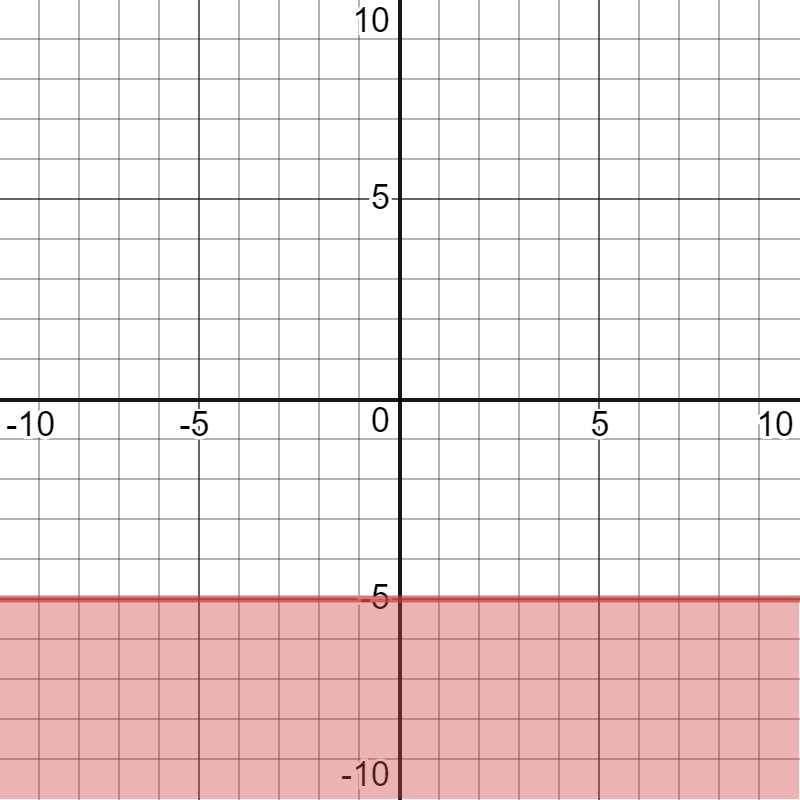
y <= -5
100
Simplify. Your answer should contain only positive exponents.
(m4)( 2m-3)
2m
100
3/5 + 2/11
3/5 + 2/11
= 33/55 + 10/55
=43/55
100
Solve for x and y.
2x − 3y = −1
y = x − 1
(4, 3)
100
32+5 = 32 + 35
FALSE
3^(2+5) = 3^2 * 3^5
200
Write a system of inequalities to match the graph.
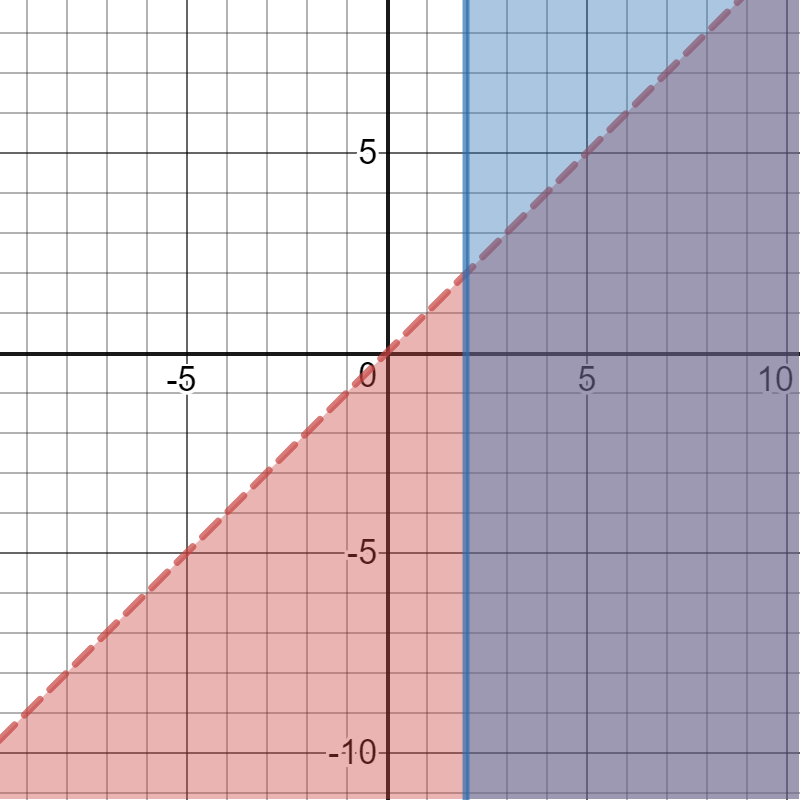
y < x
x >= 2
200
Simplify. Your answer should contain only positive exponents.
2k^4*4k
8k5
200
(7/3)2
(7/3)2
= 49/9
200
Solve for x and y
y = 6x − 11
−2x − 3y = −7
(2, 1)
200
(an)(bn) = (ab)n
TRUE
300
Write a system of linear inequalities that match the overlapping shaded region.
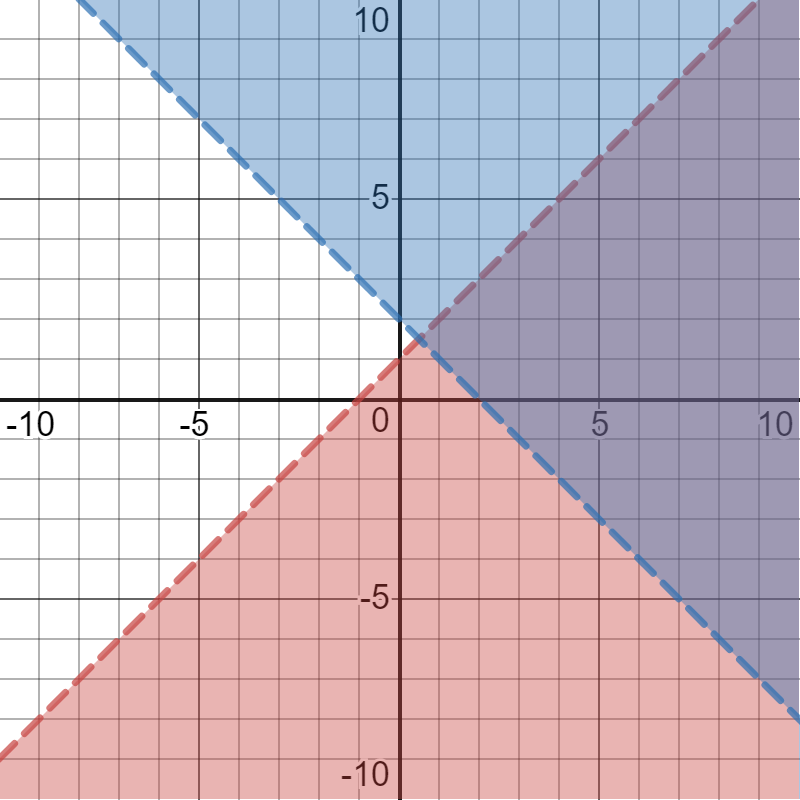
y < x + 1
y > 2- x
300
Simplify. Your answer should contain only positive exponents.
(2x^2)^-4
1/(16x8)
300
(3/1000)-1
1000/3
300
Solve for x and y
−3x + 3y = 3
−5x + y = 13
(−3, −2)
300
x ^-1 = 1/(-x)
FALSE
x ^-1 = 1/x
400
Write a system of linear inequalities that match the overlapping shaded region.
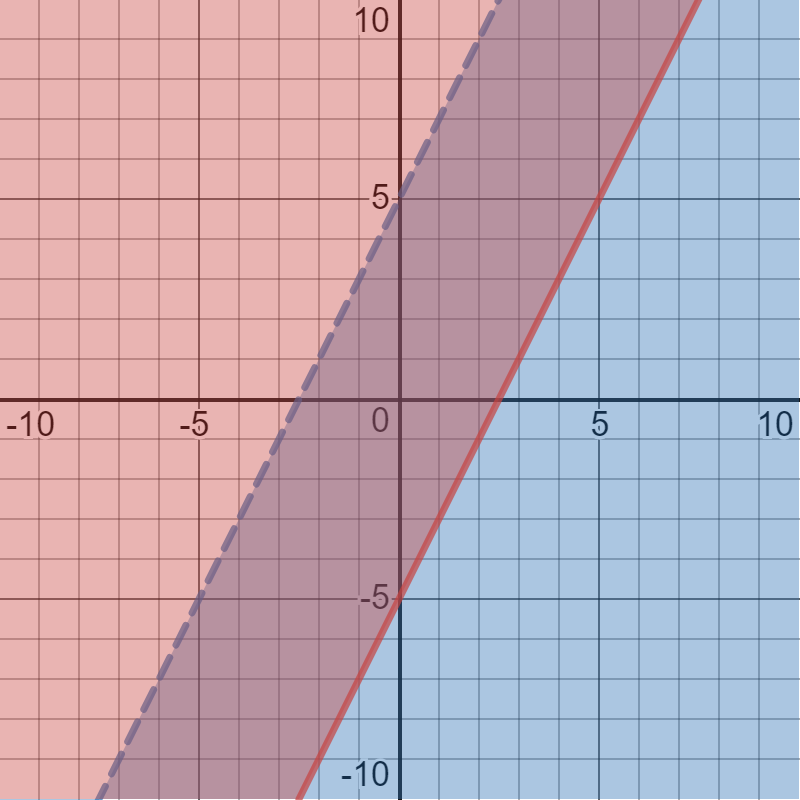
y< 2x + 5
y >= 2x - 5
400
Simplify
x (x^2)^n
x (x^2)^ n = x x^(2n) = x^(2n+1)
400
(5/2)-2
(5/2)-2
=1/(5/2)2
= 4/25
400
Solve for x and y
-5/7 - 11/7x = -y
2y = 7 + 5x
(-3, -4)
400
a0 = a
FALSE
a0 = 1
500
Write a system of inequalities whose solution is the set of all points in quadrant III, including the axes.
x <= 0
y <= 0
500
Simplify
((2xy^-1z^0)^-4*2y^-1x^3)/ (2xz^2
(y^3)/(16x^2z^2)
500
Solve
(5/6)2 - (2/3)-3
-193/72
500
The senior classes at High School A and High School B planned separate trips to New York City. The senior class at High School A rented and filled 1 van and 6 buses with 372 students. High School B rented and filled 4 vans and 12 buses with 780 students. Each van and each bus carried the same number of students. How many students can a van carry? How many students can a bus carry?
x + 6y = 372
4x + 12y = 780
(Van) x = 18
(Bus) y = 59
500
(a + b)2 = a2 + b2
FALSE!!!!!
(a + b)2 = (a + b)(a + b)