1) Define the set of prime numbers.
2) Is this set finite or infinite?
{2, 3, 5, 7, 11, 13, 17, 19, ...}
Infinite
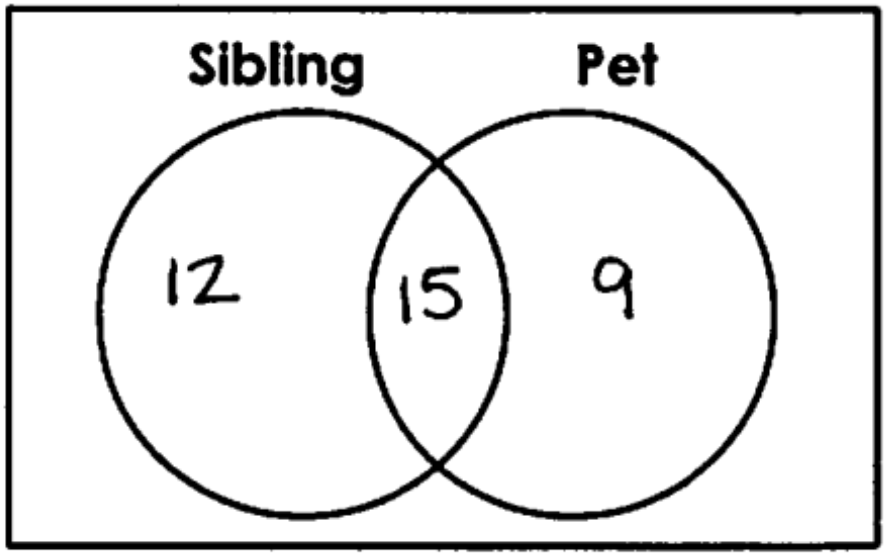
A group of students were asked if they have at least one sibling and at least one pet. Of the students surveyed, 27 said they have a sibling and 24 students said they have a pet. Of the students who said they had a sibling, 12 do not have pets. Create a Venn Diagram to display the results of the survey.
How many total outcomes are there from picking a card from a standard deck and then rolling a standard die?
312
If point X is randomly placed on \overline{JN} below, find the following probability as a fraction in simplest form:
P(X is not on \overline{LM})

9/10 or 0.9 or 90%
If a letter in the word MATHEMATICIAN is chosen at random, what is the probability of choosing a vowel?
6/13 or 0.462 or 46.2%
1) Define the set of natural numbers 1-10, inclusive.
2) Is this set finite or infinite?
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Finite
Suppose a universal set consists of natural numbers that are at most 16. Two subsets are created from the universal set; Set A contains the multiples of 3 and Set B contains the odd numbers.
Create a Venn Diagram to display the information.

How many total outcomes are possible from choosing a random answer to the last five questions on a multiple-choice test if each question has four answer choices?
1,024
If point X is randomly placed on \overline{JN} below, find the following probability as a decimal:
P(X is on \overline{JK} or \overline{MN})

13/20 or 0.65 or 65%
If a card is selected at random from a standard deck, what is the probability that it is a face card or an 8?
4/13 or 0.308 or 30.8%
Suppose a universal set consists of the multiples of 3 that are no more than 36. Two subsets are created from the universal set: Set A contains the even numbers, and Set B contains numbers that are greater than 15.
Find A\capB.
{18, 24, 30, 36}
The Venn Diagram below shows the number of boy scouts in a certain troop who have earned the following merit badges: camping, swimming, and first aid.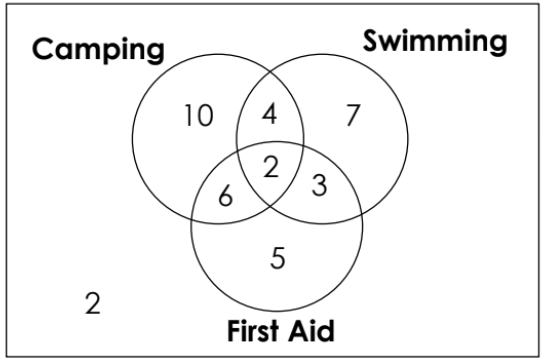
How many boy scouts do not have a camping badge?
17
If a card is selected at random from a standard deck, what is the probability that it is an ace or a red card?
7/13 or 0.538 or 53.8%
A shuttle bus arrives at a hotel every 40 minutes to take guests into town. If a guest walks out the door at a random time, find the probability of each waiting time below:
1. P(at least 15 minutes)
2. P(no more than 10 minutes)
1. 5/8 or 0.625 or 62.5%
2. 1/4 or 0.25 or 25%
A point in the figure below is chosen at random. Find the probability that the point lies in the shaded region. Give the answer as a percent.
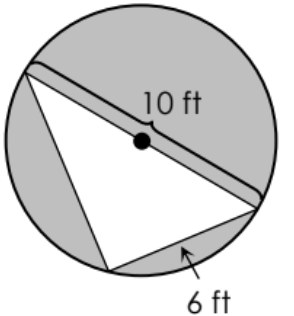
69.4%
Suppose a universal set consists of the multiples of 3 that are no more than 36. Two subsets are created from the universal set: Set A contains the even numbers, and Set B contains numbers that are greater than 15.
Find A\cupB.
{6, 12, 18, 21, 24, 27, 30, 33, 36}
The Venn Diagram below shows the number of boy scouts in a certain troop who have earned the following merit badges: camping, swimming, and first aid.
How many boy scouts have a camping badge or a swimming badge?
32
Find P(unshaded or even)
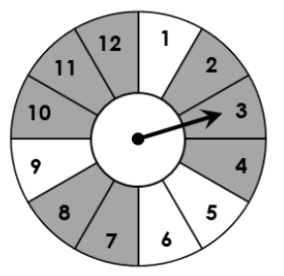
3/4 or 0.75 or 75%
A point in the figure below is chosen at random. Find the probability, as a percent, that the point lies in the shaded region. Give the answer as a percent.
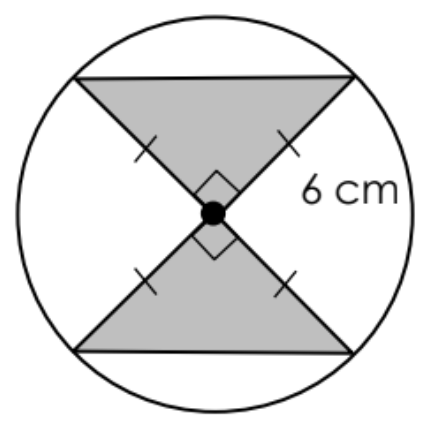
31.8%
Natalie randomly answered the last three true-or-false questions on her math quiz. What is the probability that she got at least one correct?
7/8 or 0.875 or 87.5%
Suppose a universal set consists of the multiples of 3 that are no more than 36. Two subsets are created from the universal set: Set A contains the even numbers, and Set B contains numbers that are greater than 15.
Find A'\capB'.
{3, 9, 15}
Of the 125 students enrolled at a dance studio, 96 take ballet and 50 take jazz. Of those that take ballet, 28 also take jazz. If a dance student is chosen at random, find each probability as a simplified fraction:
1. P(ballet or jazz)
2. P(ballet but not jazz)
3. P(neither ballet nor jazz)
1. 118/125
2. 68/125
3. 7/125
The spinner below is spun twice, then a card from a standard deck is chosen at random. How many different outcomes are possible?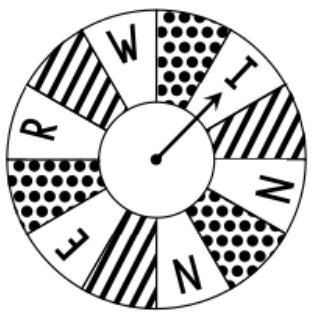
364
A point in the figure below is chosen at random. Find the probability, as a percent, that the point lies in the shaded region. Give the answer as a percent.
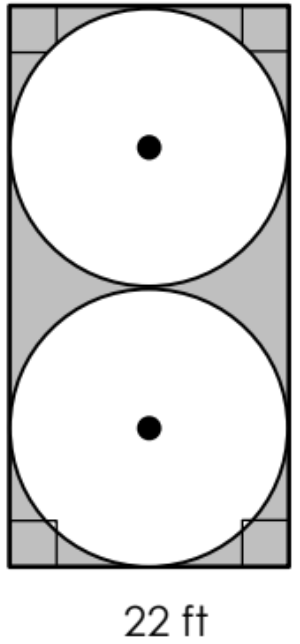
21.5%
A point in the figure below is chosen at random. Find the probability that the point lies in the shaded region. Give the answer as a percent.
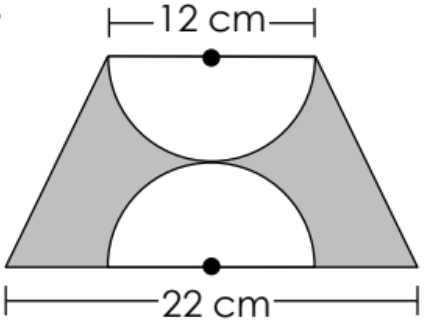
44.6%