Barry is playing bowls. He rolls his bowl towards the jack (white ball), they then collide and travel in different directions. Describe the velocity of the centre of mass before, during and after the collision.
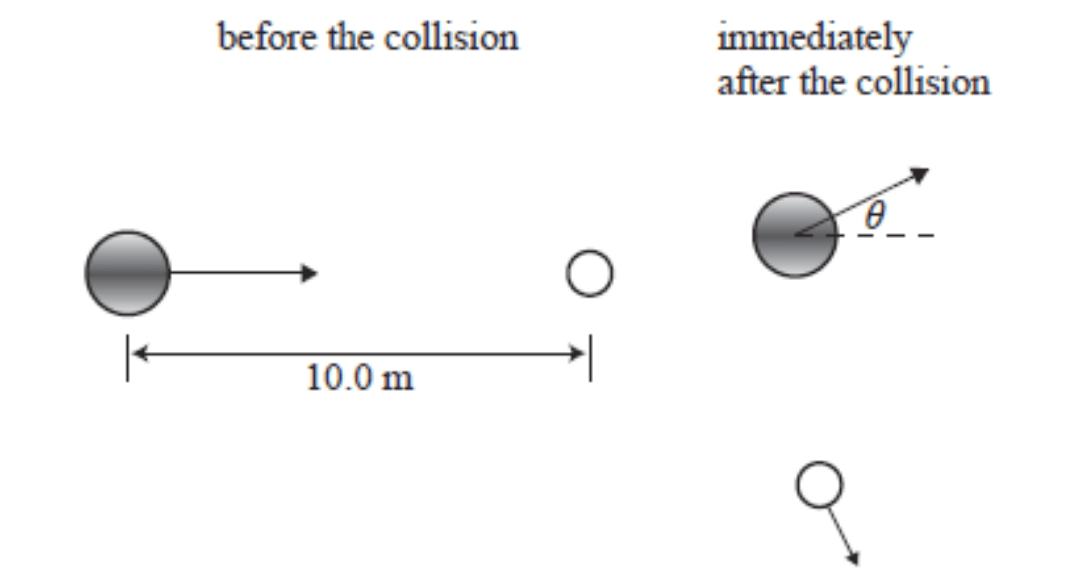
The velocity of the centre of mass is constant, assuming there are no external forces. The velocity of the centre of mass is horizontal to the right before the collision, so will continue in that direction after.
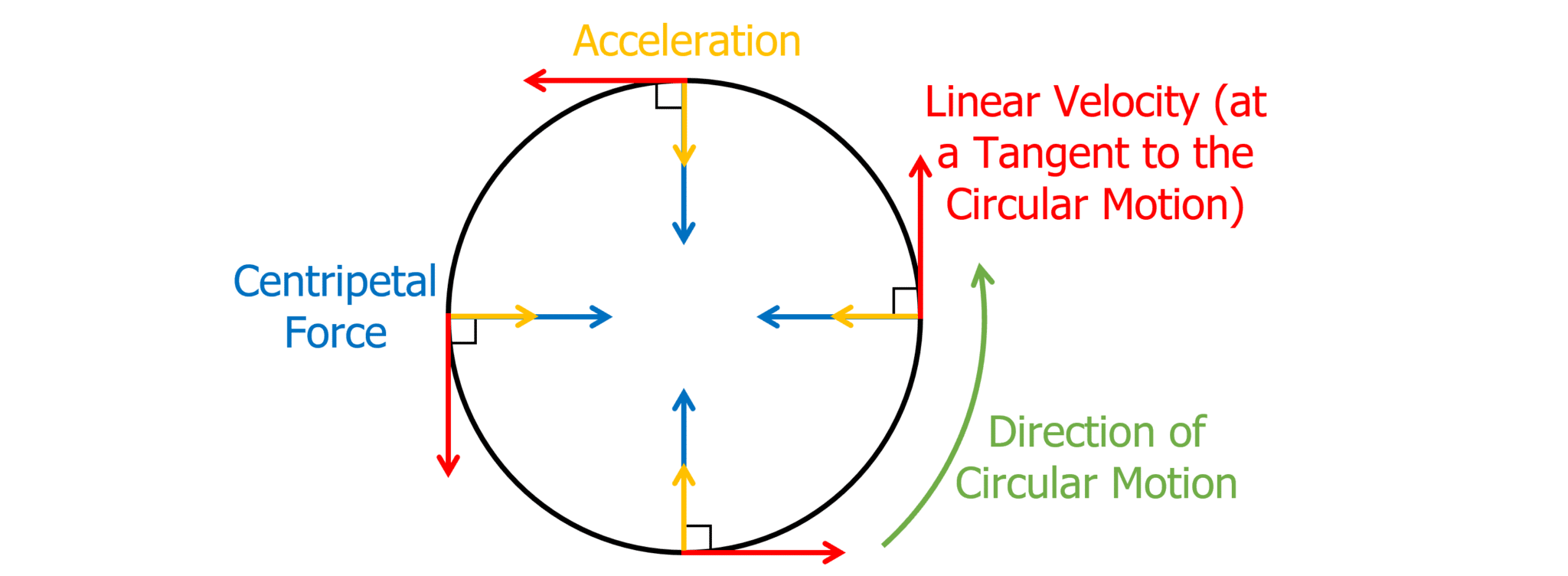
Draw a circle to represent the circular motion of the hammer. Label which direction velocity, acceleration and force are acting at a certain moment.

Velocity is at tangent to the circle. Acceleration and force are towards the centre.
A records spins at 45rpm (revolutions per minute), what is its angular velocity?

45rpm / 60 = 0.75 Hz or rev's per second
ω = 2𝞹 x 0.75 = 4.71rads-1 (3sf)
For something to be considered as moving in simple harmonic motion, what conditions must it meet?
See if you can use a relevant formula to back this up.
a = -ω2y
Acceleration (and/or force) is proportional to displacement and in the opposite direction to the displacement (i.e. towards equilibrium).
Find the centre of mass of the black bowl (1.5kg) and the white jack (0.25kg).
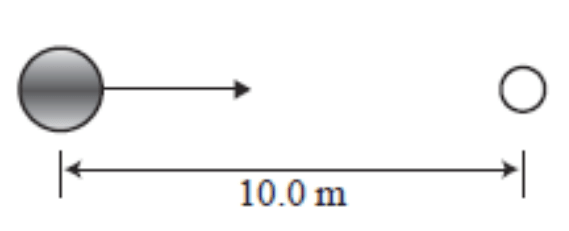
dcom = (m1d1 + m2d2) / (m1+ m2)
dcom = (1.5x0 + 0.25x10) / (1.5 + 0.25)
dcom = 2.5 / 1.75 = 1.43m (3sf) from the bowl
OR 8.57m from the jack
A toy car travels around a vertical loop as shown.
a) Draw in arrows showing the forces acting on it (direction and size) at the bottom and top of the loop
b) Explain why it is faster at the bottom of the loop (using energy)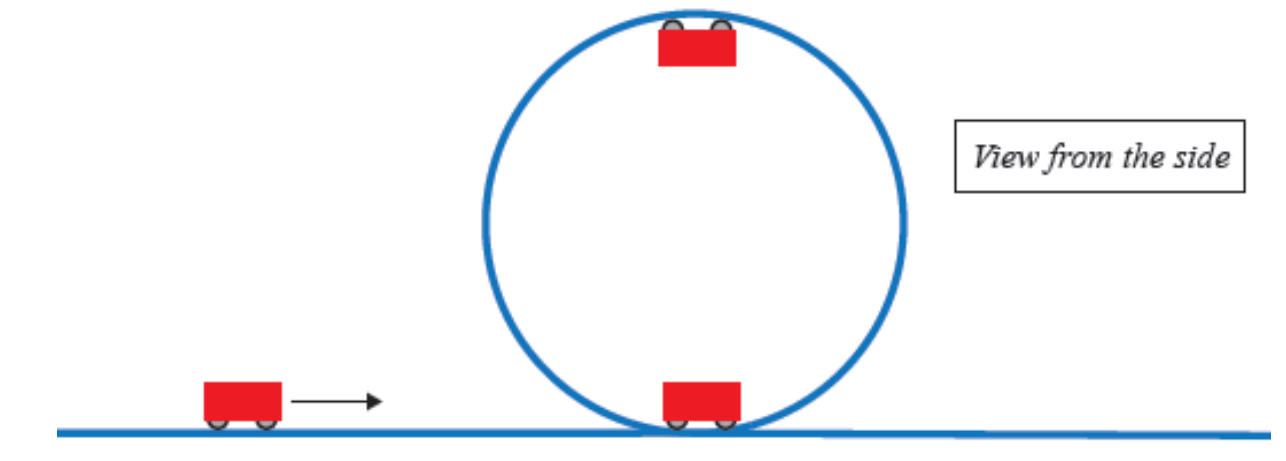
a) 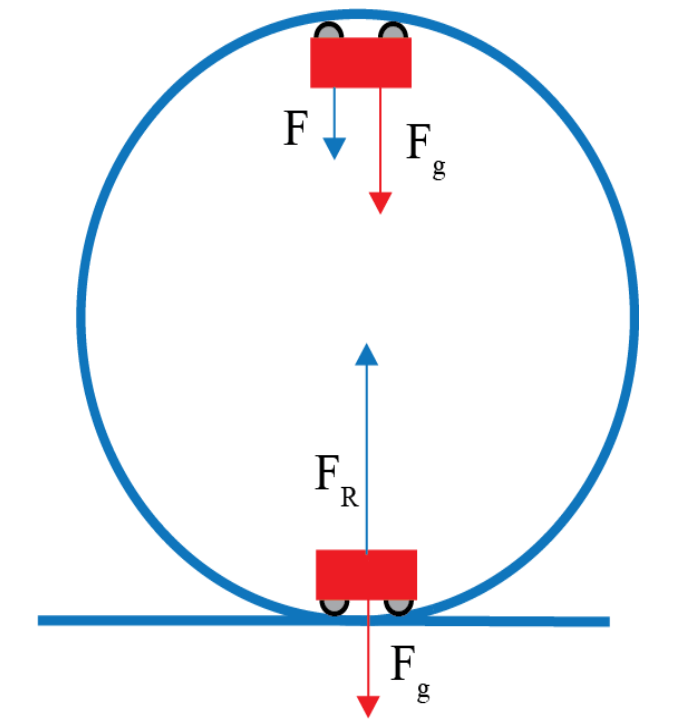
b) As the car goes around the loop energy is conserved and transforms between gravitational potential energy and kinetic energy. At the bottom, potential energy is at its minimum and kinetic energy is at its max, meaning it is traveling the fastest at that point.
A spin dryer in a clothes dryer machine has a torque operating on it of 0.4 Nm, causing an angular acceleration of 1.2 rad s-2. What is the rotational inertia of the spinning part of the dryer?
τ = Iα --> I = τ /α
I = 0.4/1.2 = 0.3 kgm2
Buildings have a resonant frequency, a frequency that they naturally vibrate back and forth at. What would happen if an earthquake had a similar frequency to a building's resonant frequency. Name and explain the effect.
When a driving force matches the resonant frequency of an oscillating object, the amplitude of the simple harmonic motion increases. This is called resonance. This would cause the buildings to sway back and forth with a greater displacement, causing more damage.

How far away from the pivot must Peter be sitting for the see saw to be balanced?

dcom = (m1d1 + m2d2) / (m1+ m2)
0 = (25x-2 + 20d2) / (25 + 20)
0 = -50 + 20d2
50 = 20d2 ---> d2 = 50/20 = 2.5m
A ball is swung in a vertical circle when attached to a 1.2m length of rope. The mass of the ball is 0.250kg. Show that the minimum speed it must be travelling at the top of the circle is 3.43ms-1 in order to stay in circular motion.
When velocity is minimum at top: Fc = Fg
Fg = mg = 0.250 x 9.81 = 2.4525N
Fc = (mv2) / r --> 2.4525 = (0.250 x v2) / 1.2
2.943 = 0.25v2
11.772 = v2 --> v = 3.43ms-1
The rotating solid cylinder shown has a radius of 0.22m and a mass of 0.86 kg. For a cylinder like this the rotational inertia is given by the equation I = ½mr2. It has a time period of 0.32s for one rotation. What is its angular momentum?
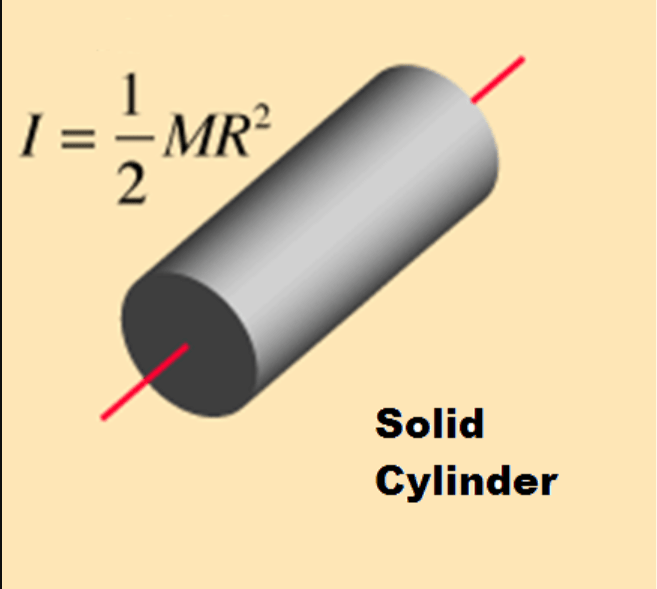
L = Iω
I = ½mr2 = ½ x 0.86 x 0.222 = 0.020812 kgm2
f = 1/T = 1/0.32 =3.125Hz --> ω = 2𝞹 x 3.125 = 19.63495 rads-1
L = 0.020812 X 19.63495 = 0.409 kgm2s-1 (3sf)
Fernando bounces on a diving board in simple harmonic motion. He travels 0.30m from the top to the bottom of his oscillation. He has a mass of 80kg and the spring constant of the diving board is 3200 Nm-1. What is his maximum velocity?
vmax = Aω
A = 1/2 x 0.30 = 0.15m
T = 2𝞹 x √ (80/3200) = 0.993459s --> f = 1/T = 1.00658 Hz --> ω = 2𝞹 x 1.00658 = 6.324555 rads-1
vmax = 0.15 x 6.324555 = 0.949ms-1
Caleb (m = 85.0 kg) and Steven (m = 115 kg) collide into each other in their bumper cars, each bumper car has a mass of 225 kg. Find their total momentum (remember units!).
ptotal = 1470kgms-1
When adding vectors, you must make a vector triangle and, in this case, use Pythagoras to find the total.
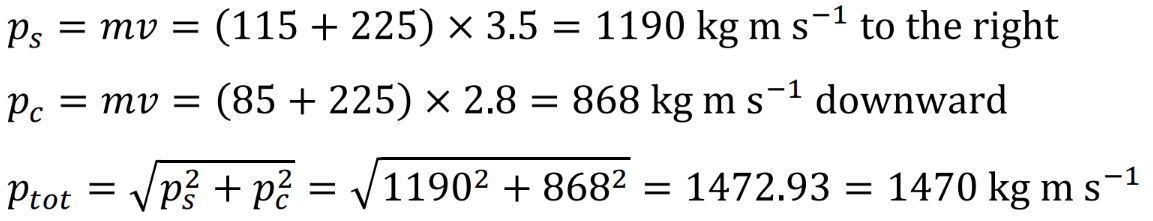
A satellite of 150kg is orbiting the Earth at a radius of 7.25 x 106 m. What is the velocity of the satellite as it orbits?
Mass of the Earth = 5.97 x 1024 kg
FC = Fg --> v = √(GM/r)
v = √( (6.67x10-11 x 5.97 x 1024 ) / 7.25 x 106 )
v = 7,410 ms-1 or 7.41 x 103 ms-1(3sf)

A spaceship, with a rotational inertia of 5.80x104 kgm2, spins anti-clockwise with an angular velocity of 0.450rads-1. Its photo-voltaic cells are extended out, causing its rotational inertia to increase by 2.74x103 kgm2. What is its new angular velocity?
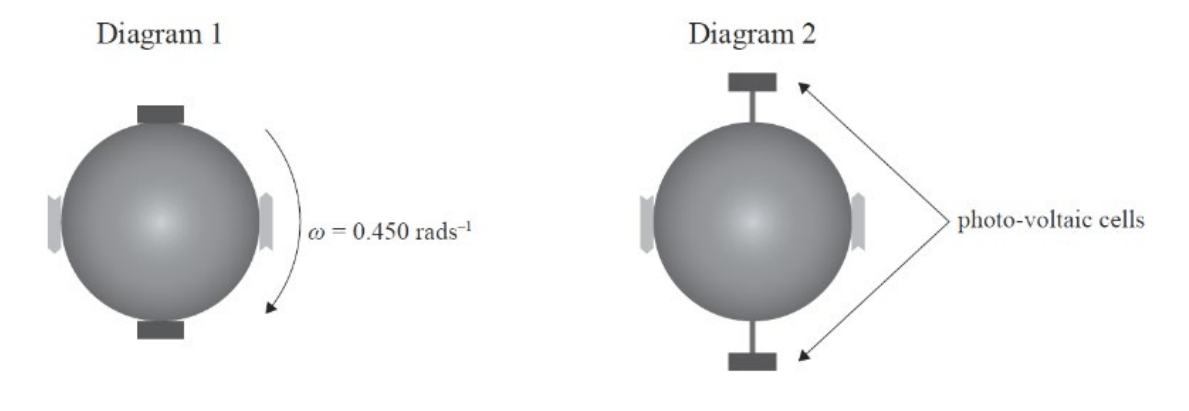
Assuming there are no external torques, angular momentum will be conserved --> Lbefore = Lafter
Lbefore = Iω = 5.80x104 x 0.450 = 26,100 kgm2s-1
ω = L / I = 26100 / (5.8x104 + 2.74x103) = 0.430rads-1
Jimmy is swinging with an amplitude of 0.58m on a swing with a time period of 2.4s. He stops using his legs to keep at a steady amplitude when he reaches max displacement. Draw his displacement for the next 3 periods on a graph, including values where possible.
Bonus points: what is the phenomenon called and what causes it?

You should start the wave at max displacement, with the value 0.58m there. The amplitude should be decreasing as time goes on, but the period of the oscillation should stay the same. Values for the time after each full cycle should be there (2.4 / 4.8 / 7.2s).
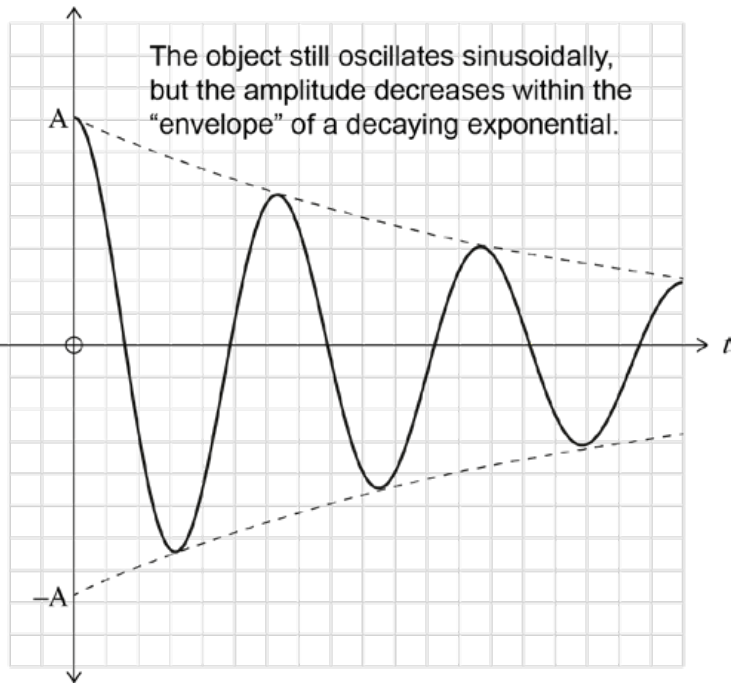
Bonus points: this phenomenon is called damping and is caused by external forces (like friction), causing energy to be 'lost' to the surroundings, through heat and sound.
Barry rolls a bowl (1.5kg) towards the jack (0.25kg) at a velocity of 6ms-1. After they collide, they travel away from each other at right angles. The bowl then has a velocity of 4.5ms-1, find the velocity of the jack.
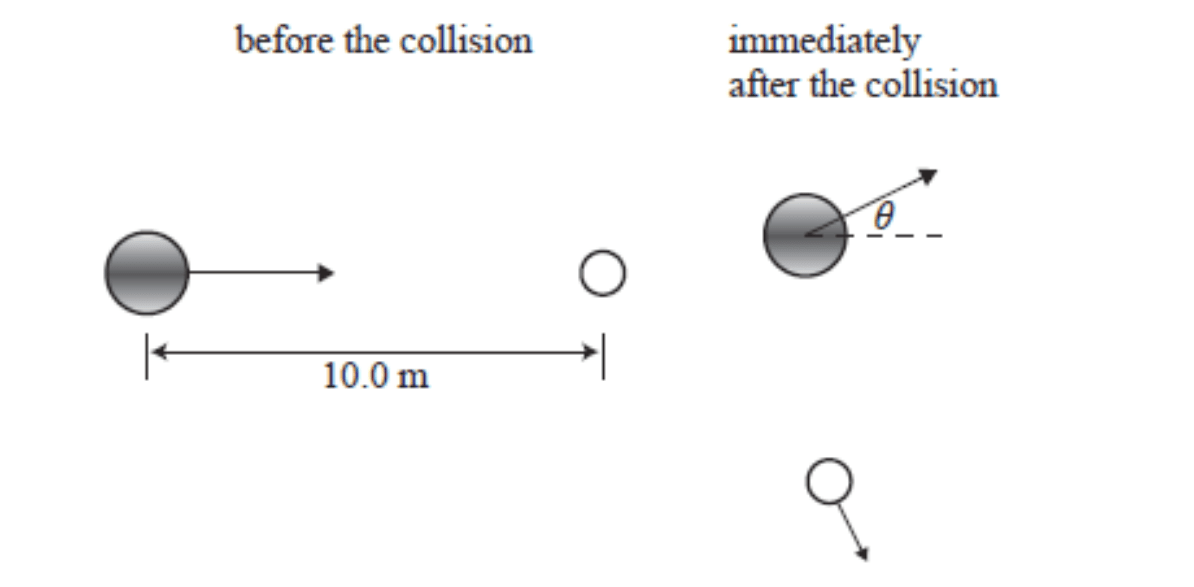
Total momentum before = total momentum after (assuming no external forces i.e. friction)
pbefore = mv = 1.5 x 6 = 9kgms-1
After: pbowl = 1.5 x 4.5 = 6.75kgms-1
92 = 6.752 + pjack2
pjack = √(92 - 6.752) = 5.95kgms-1
vjack = p/m = 5.95 / 0.25 = 23.8ms-1 (3sf)
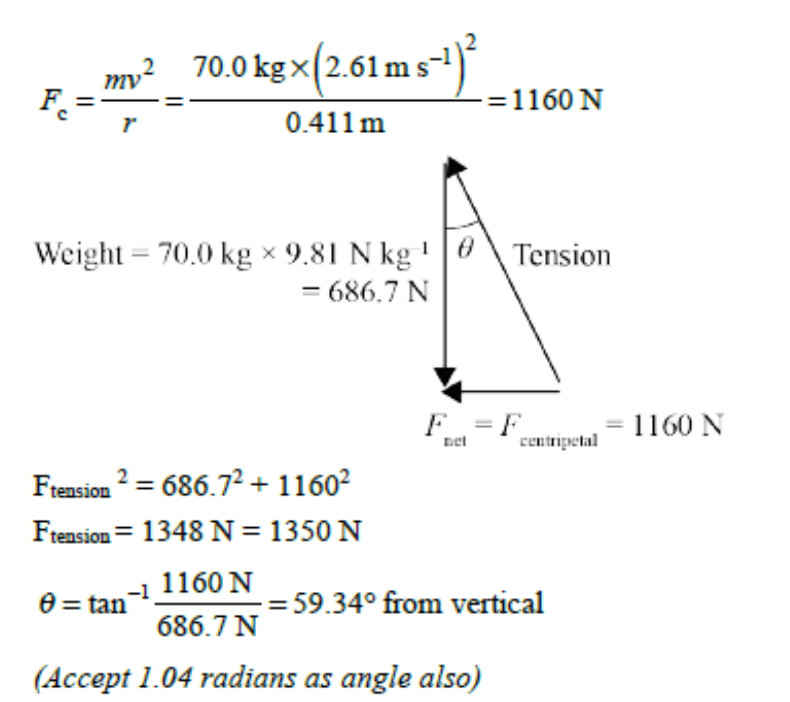
Jay swings around on a tyre swing attached by a chain to a pole, it acts as a conical pendulum. Jay swings at 2.61ms-1 with a radius of 0.411m. Jay and the tyre have a mass of 70kg. Assuming the chain has negligible mass and there are no external forces, what is the tension force provided by the chain. Bonus points if you get the angle too!
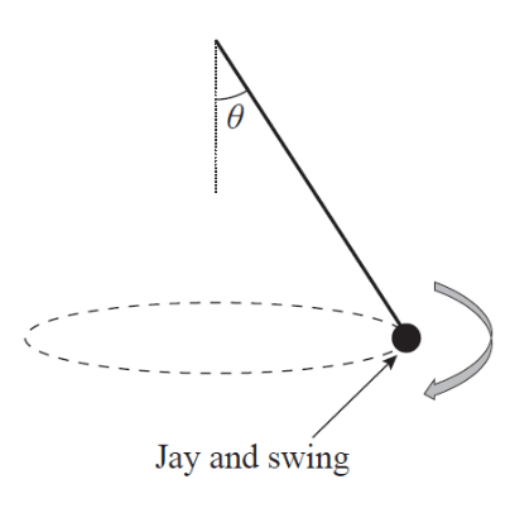
FT = 1350N at 59.3° to the vertical
An ice skater spins with their arms out wide initially; they then bring their arms in closer to their body. Explain what this will do to the rotational kinetic energy of the ice skater and state any assumptions made.
Assuming there are no external torques acting on the ice skater, angular momentum will be conserved. As the skater brings their arms in closer, they will reduce their rotational inertia, because their mass is now distributed closer to their centre of rotation. Because L=Iω, a decrease in rotational inertia will result in an increase in angular velocity. Ek(ROT) = 1/2Iω2, even though I has decreased, because ω is squared, its increase causes an increase in rotational energy for the skater.
(BONUS POINT: this added energy was provided by the work done by the skater to bring their arms in closer).
Penelope pulls down this toy (with period of 1.99s) to a displacement of 0.100m from equilibrium and releases it. Calculate how long it would take for the toy to go 0.140m up from where it was released.

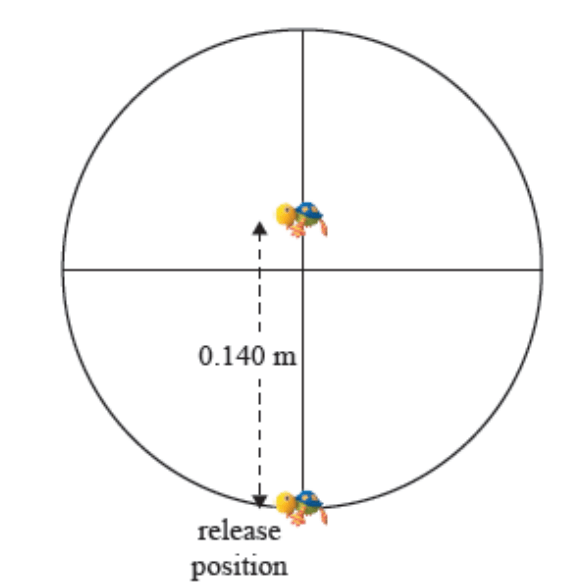
y = A cos (ωt)
y = -0.040m (because it is on the other side of equilibrium)
A = 0.100m
ω = 2𝞹 / T = 2𝞹 / 1.99 = 3.157380 rads-1
-0.040 = 0.100 x cos (3.157380t)
-0.040/0.100 = -0.40 = cos (3.157380t)
cos-1(-0.40) = 1.982313 = 3.157380t
t = 0.628s
