Pure Strategy Vocabulary
Saddle Point?
Insurance?
Mixed Strategy Vocabulary
Optimal Strategy
100
In a game represented in the matrix below, does the row player want the big numbers or the small numbers?
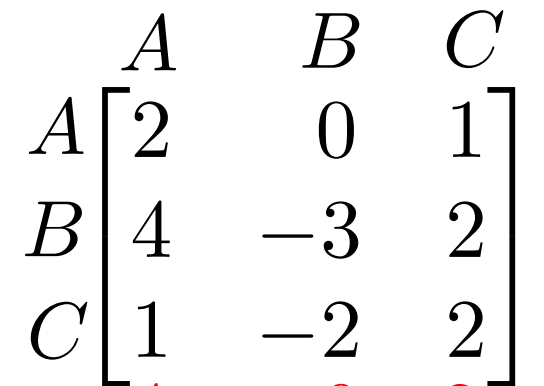
Big
100
What three things need to be equal for a game to have a saddle point?
Minimax, Maximin, Value
100
You are buying a tv, and have the chance to buy a warranty. The warranty costs $300. If your tv needs to be fixed, it will cost $200. If your tv needs to be replaced, it will cost $600. If you have the warranty, it will take care of both of these situations for no additional cost.
Who is the row player in this situation?
TV Store
100
When do you adopt a mixed strategy?
When there is no saddle point.
100
Use the scenario below to write two expected value equations that could be used to find Thomas' optimal probabilities.
E = p1(s1) + (1 - p1)(s2)
E = p1(-1) + (1 - p1)(8)
E = p1(7) + (1 - p1)(-10)
200
In a game represented in the matrix below, does the column player want the big numbers or the small numbers?
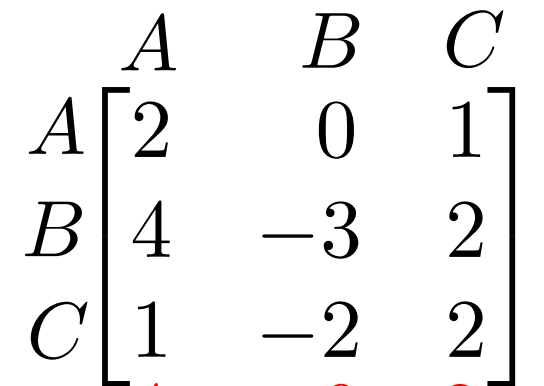
Small
200
If a game has a strategy, should you use a pure strategy or a mixed strategy?
Pure
200
You are buying a tv, and have the chance to buy a warranty. The warranty costs $300. If your tv needs to be fixed, it will cost $200. If your tv needs to be replaced, it will cost $600. If you have the warranty, it will take care of both of these situations for no additional cost.
Create a payoff matrix that represents this situation.
200
What is the expected value formula?
E = p1(s1) + (1 - p1)(s2)
200
Using your calculator, what would p1 be from the previous problem?
p1 = 0.692
300
What is the maximin of the game below?
0
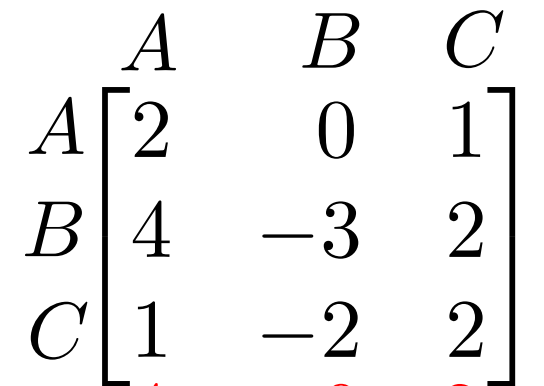
300
If a game has a pure strategy, then a player should pick that strategy _____________ of the time.
A) All
B) Some
C) None
A) All
300
You are buying a tv, and have the chance to buy a warranty. The warranty costs $300. If your tv needs to be fixed, it will cost $200. If your tv needs to be replaced, it will cost $600. If you have the warranty, it will take care of both of these situations for no additional cost.
What is the maximin?
$300
300
What does p1 stand for in the equation E = p1(s1) + (1 - p1)(s1)?
The optimal probability that a player should use to select strategy 1.
300
What would p2 be in this problem?
1 - 0.692 = 0.308
400
What is the minimax of the game below?
0
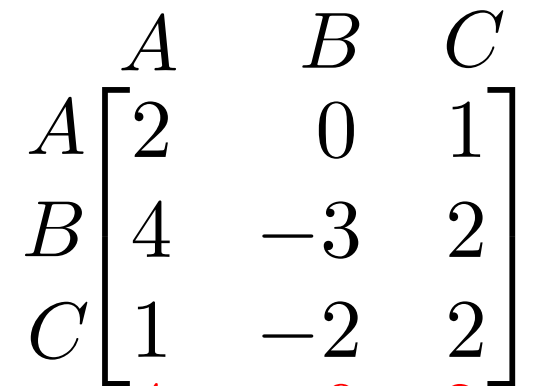
400
Does this game have a saddle point? Why or why not?
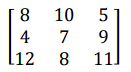
No, the minimax does not equal the maximin or the value.
Maximin = 8
Minimax = 10
Value = 8
400
You are buying a tv, and have the chance to buy a warranty. The warranty costs $300. If your tv needs to be fixed, it will cost $200. If your tv needs to be replaced, it will cost $600. If you have the warranty, it will take care of both of these situations for no additional cost.
What is the minimax?
$300
400
In a two strategy game, if the optimal probability for strategy 1 is 0.65, what is the optimal probability for strategy 2?
1 - 0.65 = 0.35
400
Is this a fair game? Why?
Not fair, the expected value is 1.769 which is not zero.
500
Does this game have a saddle point? If so, what is it?
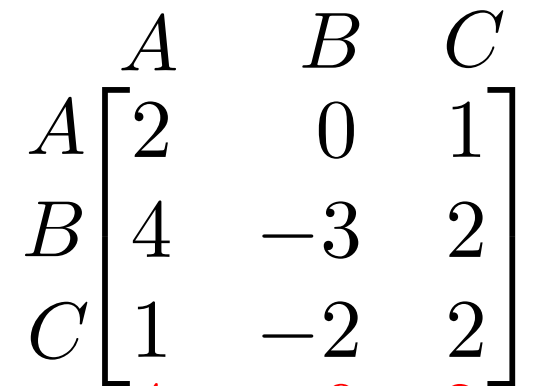
Yes, 0
500
Does this game have a saddle point? Why or why not?
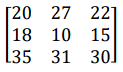
Yes, minimax = maximin = value = 30
500
You are buying a tv, and have the chance to buy a warranty. The warranty costs $300. If your tv needs to be fixed, it will cost $200. If your tv needs to be replaced, it will cost $600. If you have the warranty, it will take care of both of these situations for no additional cost.
What is the outcome of this "game"?
You buy insurance.
500
If the expected value of a game is 0.5, is that a fair game? Why or why not?
Not fair, expected value is not zero. The expected value of a fair game is zero.
500
How often should Thomas select strategy 1? How often should Thomas select strategy 2?
Thomas should select strategy 1 69.2% of the time and strategy 2 30.8% of the time.