Rational Functions
Polynomial Functions
Inverse and Composite Functions
Exponential Functions
Logarithmic Functions
100
Give the domain of the function in set notation.
f(x)=(-4x^2)/(x^2+2x-8)
{x|x!=2,-4}
100
List all of the possible rational zeros for the function
f(x)=-4x^3-x^2+x+2
+-1,2,1/4,1/2
100
Find the composite function and state the domain.
f(x)=2x+1, g(x)=3x (f@g)(x)=?
(f@g)(x)=6x+1, (-oo,oo)
100
Solve
2^3=2^(x+2)
x={1}
100
Expand the logarithm:
ln((3x(x-3)^(1/5))/(x+2))
ln3+lnx+1/5ln(x-3)-ln(x+2)
200
Give the equation for all asymptotes and state what type they are (vertical, horizontal, or oblique) for the function:
R(x)=(3x+4)/(x-6)
HA: y = 3
VA: x = 6
Bonus Prize - How would you draw these on a graph?
200
Using the Intermediate Value theorem determine if there is a zero between -1 and 0. Explain why or why not.
f(x)=x^4+8x^3-x^2+2
Yes because the y-values are opposite signs.
f(-1)=-6
f(0)=2
200
Is the following function 1-to-1? Why or why not?
f(x)=3(x-2)^2+1
No because there are output (y-values) with more than one input.
For example: (1,7) and (3,7)
200
Solve:
5^(2x-3)=25^(3x)
x={-3/4}
200
Solve without a calculator:
log_3(1/27)=?
log_3(1/27)=-3
300
Give the equation for all asymptotes and state what type they are (vertical, horizontal, or oblique) for the function:
R(x)=(x-1)/[(x-1)(x+4)]
HA: y = 0
VA: x=-4
Bonus Prize 1- Removable Discontinuity (RD) at
(1,1/5)
Bonus Prize 2- How would you graph the RD?
300
Given one of the zeros is 1 find the remaining zeros using synthetic division for the function
f(x)=3x^3+24x^2+33x-60
The remaining zeros are -5 and -4.
Bonus Prize: Write the function in factored form using the zeros.
300
Find the composite function and state the domain.
f(x)=x^2+1; g(x)=sqrt(x-1); Find g@f
Domain: All real numbers
(g@f)(x)=sqrt(x^2)=|x|
300
Solve:
3^(x^2-7)=9^(3x)
x={-1,7}
300
Solve:
log_3 243=2x+1
x={2}
400
Give the equations for all asymptotes and state what type they are (vertical, horizontal, or oblique) for the function
G(x)=(x^3+1)/(x^2-5x-14)
VA: x = -2 and x = 7
OA: y = x + 5
400
Find the complex zeros of the polynomial function given one is:
5i
g(x)=x^3+3x^2+25x+75
The remaining zeros are:
-3
and
-5i
400
Find the inverse of the function
f(x)=3x+2
f^-1(x)=1/3(x-2) =(x-2)/3
400
Graph using transformation and make sure to show all important features.
f(x)=e^(x-1)+2
Please make sure you put arrows on the graph to show it keeps going, you will lose points if they are not there.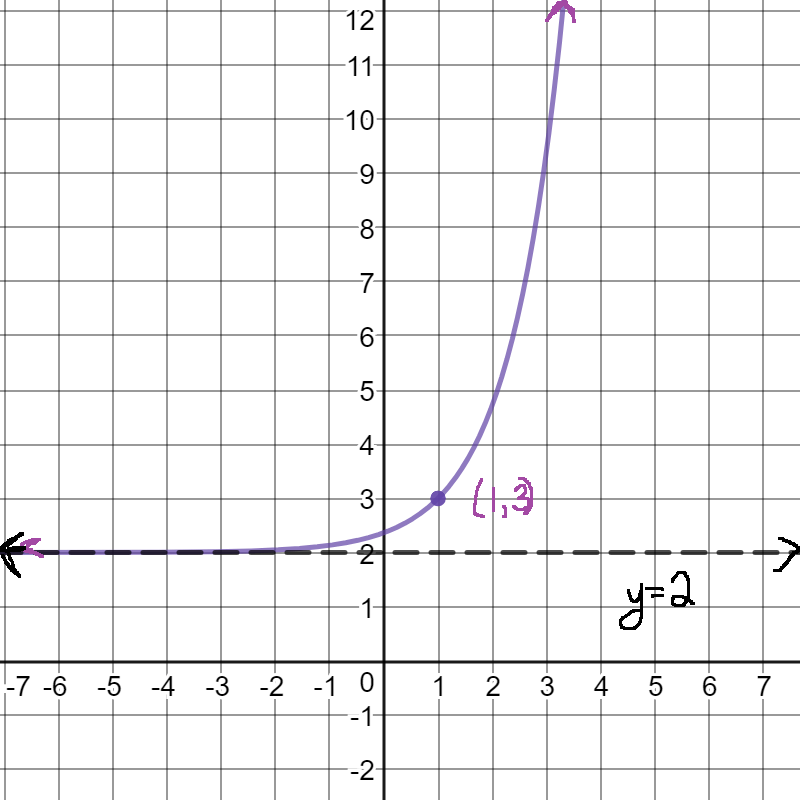
400
Graph with all important features:
h(x)=log_2 (x-1)+4
500
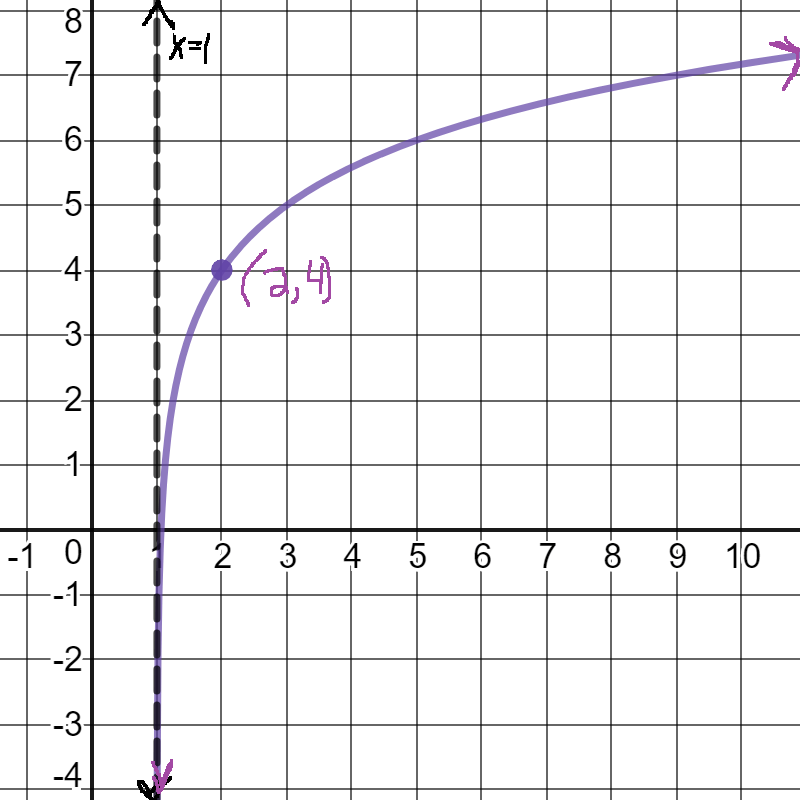
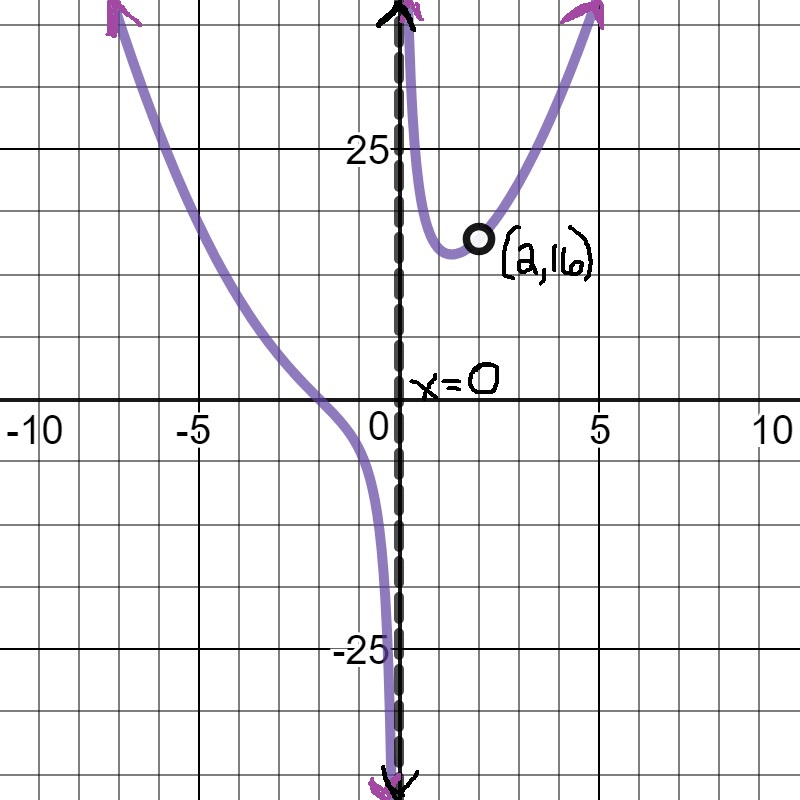
Draw the graph for the function and make sure you give all important features.
F(x) = (x^4-16)/(x^2-2x)
500
Write the polynomial in factored form using the complex zeros, One of the zeros is -3.
f(x)=2x^4+5x^3+5x^2+20x-12
f(x)=2(x+3)(x-1/2)(x+5i)(x-5i)
500
Find the inverse of the funtion
g(x)=x^2+2;x<=0
g^-1(x)=-sqrt(x-2)
500
Solve:
(e^4)^x*e^(x^2)=e^12
x={-6,2}
500
Solve and give the exact answer. If necessary use the natural log.
e^(2x+5)=8
x={(ln8-5)/2}={(-5+ln8)/2}