Work out the sum of the INTERIOR angles for a polygon with:
a. 20 sides
b. 45 sides
a. (20 – 2) × 180 = 3240°
b. (45 – 2) × 180 = 7740°
Find the value of C.
Give the answer correct to 2 decimal places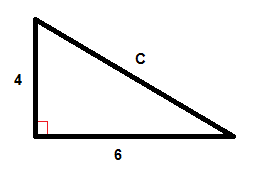
c2 = 42 + 62
c = √(16 + 36)
= 7.21
Name the sides AB, BC and AC
AB -> Adjacent
BC -> Opposite
AC -> Hypotenuse
Work out the number of sides of a polygon with the sum of the INTERIOR angles:
a. 2880°
b. 1980°
a. 2880 = (n - 2) x 180
n = 18 sides
b. 1980 = (n - 2) x 180
n = 13 sides
Find the value of x.
Give the answer correct to 2 decimal places.
202 = 142 + x2
x2 = 202 - 142
x = √(400 - 196)
= 14.28
Find the value of x.
Give your answer correct to 2 significant figure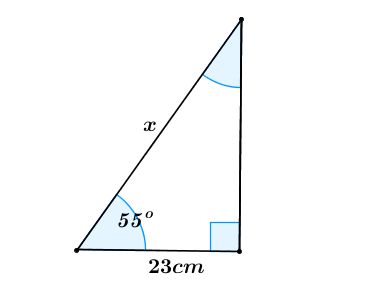
Cos 55° = 23 / x
x = 23 / Cos 55°
= 40 cm
Calculate the number of sides of a regular polygon with an exterior angle of:
a. 36°
b. 24°
a. 360 ÷ 36 = 10 sides
b. 360 ÷ 24 = 15 sides
Find the value of x and y.
52 = 32 + x2
x = √(25 - 9)
= 4
62 = 42 + y2
x = √(36 - 16)
= 4.47
Find the length of the side O.
Give your answer correct to 2 significant figures
Tan 71° = O / 6
O = 6 Tan 71°
= 17 cm
A regular polygon has an interior angle that is five times larger than its exterior angle.
How many sides does the regular polygon have?
x + 5x = 180°
6x = 180°
x = 30°
360° / 30° = 12 sides
Find the value of x
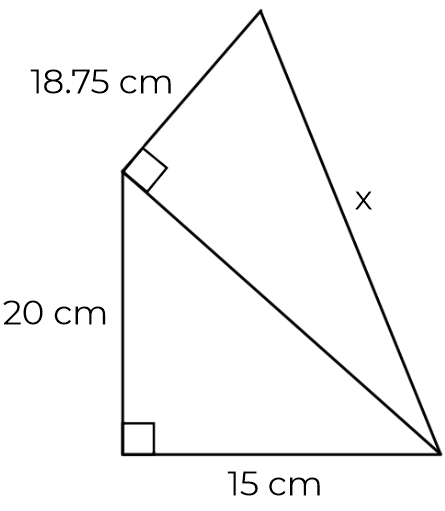
h2 = 202 + 152
h = √(400 + 225)
= 25 cm
x2 = 252 + 18.752
x = √ (625 + 351.5625)
= 31.25 cm
Find the value of x.
Give your answer correct to whole number
Tan 35° = 115 / baseB
baseB = 115 / Tan 35°
= 164 cm
Tan 56° = 115 / baseS
baseS = 115 / Tan 56°
= 78 cm
x = 164 - 78
= 86 cm

x = 126°
