The number of zeroes in the graph.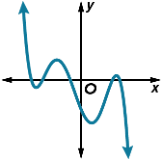
What is 5 zeroes?
The coordinates of the real zero(es) of the following function. Round to the thousandths place. f(x) = –x^3 + x^2 + 2x + 1
what is
(2.148,0) ?
The sum of (4a^2+3ab-b^2)+(b^2-2ab) .
What is
4a^2+ab?
The solution to (35y^8-80y^7+15y^6-25y^5 ) (5y^4 )^{-1}
What is 7y^4-16y^3+3y^2-5y ?
The first nine rows of pascals triangle.
1, 1 1, 1 2 1, 1 3 3 1, 1 4 6 4 1, 1 5 10 10 5 1, 1 6 15 20 15 6 1, 1 7 21 35 35 21 7 1, 1 8 28 56 70 56 28 8 1, 1 9 36 84 126 126 84 36 9 1
The number of zeroes and end behavior of the graph.
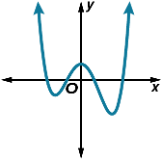
4 zeroes and as
x\rightarrow-\infty , f(x)\rightarrow \infty
x\rightarrow \infty , f(x)\rightarrow \infty
The coordinates in which relative maxima occur of the following function. Round to the nearest hundredths place.
f(x) = –2x^3 + x^2 + 10x – 5
What is a relative minimum of (-1.14,-12.14) and a relative maximum of (1.47,5.51) ?
Subtract: (3x^2-2xy+4y^2 )-(2x^2+3y^2) .
What is
x^2-2xy+y^2?
The quotient of (a^3+4a^2-9a-36) and (a+4) .
What is a^2-9 ? Or
(a+3)(a-3)
The binomial expansion of (f + g)^5
What is
f^5+5f^4g+10f^3g^2+10f^2g^3+5fg^4+g^5?
The following polynomial in standard form, classified, and state the leading coefficient.
8y + 7y^2 – 9y^3 – 15y^4
What is
-15y^4-9y^3+7y^2+8y
,quartic polynomial, and a leading coefficient of -15?
The coordinates in which relative maxima occur of the following function. Round to the nearest hundredths place.
f(x) = 5x^7+2x^4-7x^3-12
What is a relative minimum of (0.8,-13.7) and a relative maximum of (-0.95,-7.86) ?
The product of (a + b) and (a^3 – 3ab – b^2)
What is a^4+a^3b-3a^2b-4ab^2-b^3 ?
The quotient of (x^2-x-12)/(x-4) using factoring and cancellation property. VERIFY using long division.
What is ((x-4)(x+3))/(x-4) or (x+3) ?
The binomial expansion of (2m – 3n)^3
What is 1(2m)^3+3(2m)^2(-3n)+3(2m)(-3n)^2+(-3n)^3 or 8m^3-36m^2n+54mn^2-27n^3 ?
The leading coefficient, degree, domain, and range of the following function:
f(x) = 4x^3
Leading Coefficient: 4
Degree: 3
Domain:
{x|x\in \mathbb{R}} or (-\infty,\infty)
Range:
{f(x)|f(x)\in \mathbb{R}} or (-\infty,\infty)
The owner of a bicycle shop models the shop’s profit in thousands of dollars each year by using the formula p = 0.015x^3– 0.2x^2 + 0.95x + 39 , where x is the number, in hundreds, of bicycles sold. The profit that the company will make if the company sells thirty bikes.
What is $292,500 or 292.5 thousand dollars?
The product of (a + b) , (2a + 3b) , and
(2x – y)
What is 4a^2x-2a^2y+10abx-5aby+6b^2x-3b^2y ?
The quotient using synthetic division. (2t^2-13t-22)(t-8)^(-1)
What is 2t+3+2/(t-8) ?
The setup of the binomial expansion of
(7w + 4z)^5
What is (7w)^5+5(7w)^4(4z)+10(7w)^3(4z)^2+10(7w)^2(4z)^3+5(7w)(4z)^4+(4z)^5 ?
CONSTRUCTION The owners of a home are building a rectangular patio behind their house. The function f(x)=-x^2 +18x models the area in square feet of the patio, where x is the length of one side of the patio.
Find the area of the patio if the owners choose 7 feet for the length of side x.
What is
77 ft^2 ?
The manager of a coffee shop wants to evaluate the effectiveness of discount coupons distributed in the community. The number of customers who visit the shop can be modeled using the formula c = 0.000003x^3+ 65 , where x is the number of coupons distributed. The description of the relevant domain.
What is if x is the number of coupons distributed, then the relevant domain is only positive integers? (we cant owe a coupon or receive a fraction of a coupon)
The volume of the following box. V=lwh

What is
V=(s)(s+2)(s+3)=(s^2+2s)(s+3)=s^3+5s^2+6s?
The height of the sail with
6x^2+7x+2?
using the formula A=1/2bh . *Hint*
h=(2A)/b

What is
h=4x+6?
Mateo flips a coin 8 times. The coin lands on heads 3 times and tails 5 times. If the coin is equally likely to land on heads or tails, find the probability of this outcome by expanding (h + k)^8 . Round to the nearest percent if necessary.
What is h^8+8h^7k+28h^6k^2+56h^5k^3+70h^4k^4+56h^3k^5+28h^2k^6+8hk^7+1k^8 ? And 22% ?