True or False: As effect size increases, power decreases.
False; as effect size increases, power also increases.
When fitting a smoothed spline term, how many parameters are estimated?
None! There are no β parameters involved, it is estimated in a nonparametric fashion.
From an experimental design perspective, what is the gold standard for establishing causal relationships?
Randomized experiments
As the sample sizes increases, how does that affect the influence of the prior on the posterior distribution?
The larger the sample size, the smaller the influence of the prior on the posterior.
Provide a definition for statistical power.
Power is the probability of detecting an effect, given that there is an effect present.
Put another way, power is the probability of correctly rejecting the null hypothesis (given that it is false).
What is indicated by the p-value associated with a smooth term?
The p-value indicates whether this effect is significantly different from a horizontal line.
*Note: This test should not be overemphasized as it is fairly easy to achieve significance -- visual exploration of the trajectory is the main criterion.
True or False: We cannot make causal claims based solely on data.
True - We cannot prove causality with statistics since causal relations cannot be established in a purely data-driven way.
What are elicited priors?
Eliciting priors involves designing priors based on previous studies and/or expert knowledge.
These substantively motivated priors are a special type of informative priors. Basically, one inserts information that researchers have available.
Most often elicited priors incorporate information about μ (i.e., we abandon the 0=μ restriction).
We're running a t-test with 50 participants in each group. Based on the power curves below, what is our power to detect a medium size effect.
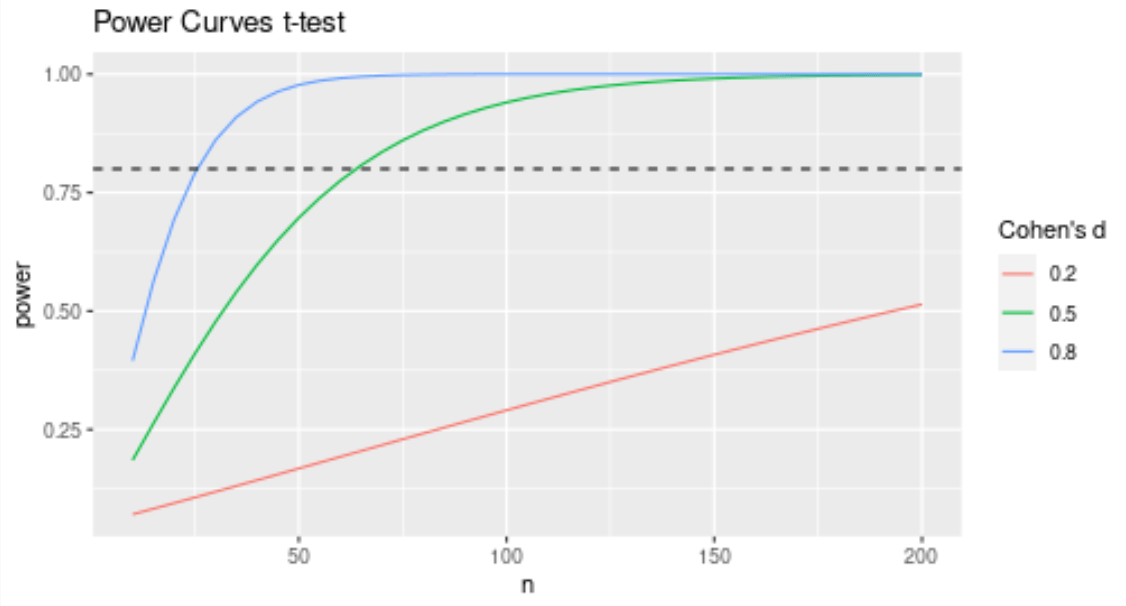
We have a power of approximately .70 to detect a medium effect. (i.e. around 70% of the time we correctly reject the null hypothesis).
What is the difference between GLMs and GAMs?
GLMs are all about the distribution of the response variable. The main selling points of GLMs are their flexibility in response distributions.
GAMs are defined for the same distributions as GLMs. The difference lies in the predictors (i.e., smooth vs. linear terms). GAMs relax the assumption of linear effects for metric variables in regression, combining parametric and non-parametric effects.
What is the fundamental problem of causal inference?
To make causal claims with 100% confidence we would have to observe both potential outcomes: the factual and counterfactual. The fact that we don't observe the counterfactual state is commonly referred to as the fundamental problem of causal inference.
Come up to the board and draw three prior distributions (centered around zero) which are non-informative, weakly informative, and informative.
Label these distributions accordingly.

What are the four ingredients for any power analysis?
B - Beta error (Type II error, typically set to .80)
E - Effect Size
A - Alpha error (Type 1 error, typically set to .05)
N - Sample Size (n)
When should we go with a GAM?
1. We don't want to assume a linear effect for a metric predictor X on Y (confirmatory).
2. We let the data decide if a nonlinear effect is needed or not (model comparison; exploratory).
3. A scatterplot shows a potential nonlinear relationship between a metric predictor X and Y.
What are the two core assumptions in Rubin's potential outcomes framework?
Ignorability: assumes that whether or not someone recieves the treatment doesn't depend on how they would respond to the treatment.
Stable Unit Treatment Value Assumption (SUTVA): assumes that assigning treatment to one person doesn't affect the outcome for another person (no spillover effects), and that everyone gets the same kind of treatment (consistent in its administration).
Provide two motivations for changing priors from the default (non-informative) priors.
1. Specifying more informative priors takes a somewhat more conservative approach for hypothesis testing: the model shouldn't get too excited about the data.
2. We can incorporate information from previous studies or other sources of expertise.
3. Specifying informative priors helps the estimation algorithm (MCMC)