Function Ops
Compose Yourself
Transformers
How Odd? (or is it?)
Ch-Ch-Ch-Changes
100
What is
4x^3-6x^2+13x-62?
100
f(g(3))
when
f(x)=x^2+3x-70
and
g(x)=4(x-3)
What is
-70?
100
In function notation: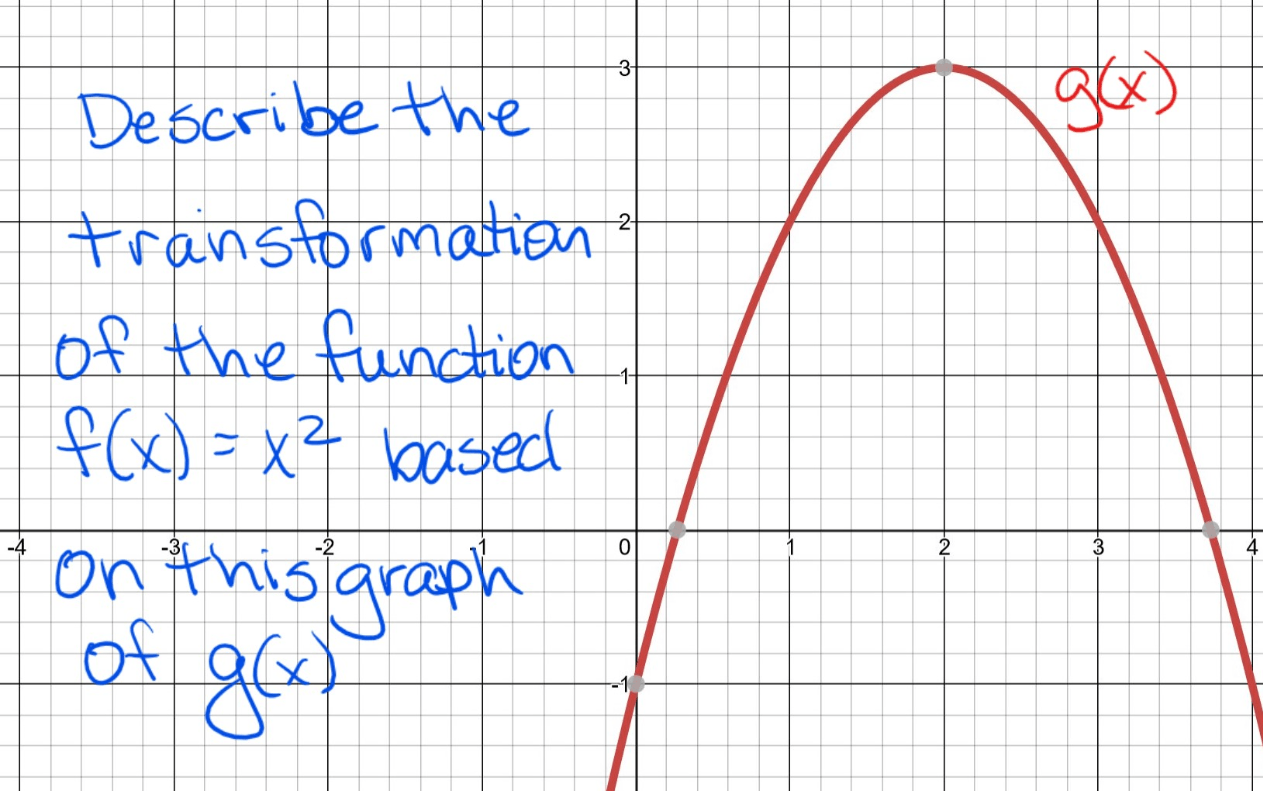
What is
g(x)=-(x-2)^2+3
100
The graph of an odd function must do this.
What is: be symmetrical about the origin.
100
In linear functions, the rate of change is_______
and the rate of change in non-linear functions is either ___________ or ____________.
1. constant.
2. increasing.
3. decreasing.
200
Three polynomial functions are given:
f(x)=3x^2+5x-z
g(x)=5x^2-3x+z
m(x)=2x^2-2x
The sum of:
f(x)+[g(x)-m(x)]
What is
6x^2+4x or 2x(3x+2)?
200
Given two functions,
f(x) and g(x)
Under this condition
f(g(x))=g(f(x))
What is,
f(x) and g(x)
are inverses?
200
The variables affected on the following transformation and what the effect is:
c(x)=f(x)+8
g(x)=f(x-4)+9
r(x)=f(1/4x)
w(x)=-2(x-2)-3
What is:
c(x) affects the dependent variable; moves up 8 units.
g(x) affects the independent variable moving 4 units right and the dependent variable moving 9 units up.
r(x) affects the independent variable with a horizontal stretch by a factor of
1/4
w(x) affects the independent and dependent variables with a move right 2 units, vertical stretch by a factor of 2, reflection about the x axis and down 3 units.
200
When considering odd, even or neither, the function
x^3+x
is this:
What is odd
200
The type of functions represented by the tables:
g(x) is linear
h(x) is quadratic
j(x) is exponential
300
The values for
a, b, c, d, and e
when
when f(x)*g(x)=ax^4-bx^3-cx^2+dx-e
f(x)=(x^2+7x-12) and g(x)=(x^2-9x+1)
What is
a=1, b=2, c=74, d=115, e=12
300
Given
f(x)=7x
g(x)=sqrt x
h(x)=x^2+7
The composition of
f(h(x))
What is
7x^2+49?
300
The values for r(x) given that
r(x)=j(x)-5,
when x = -6, -4, -3, -1, 1
What are
x y
-6 2
-4 -6
-3 -7
-1 -3
1 9
300
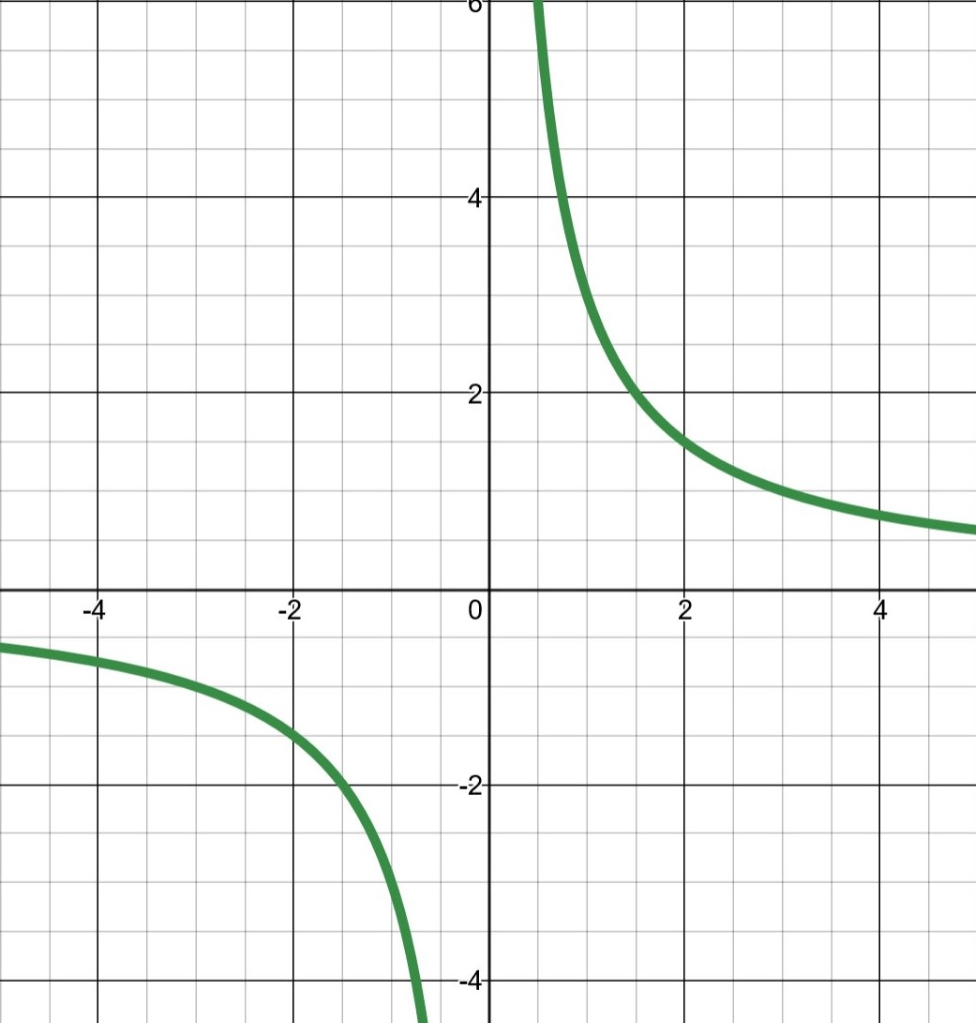
What is odd?
300
The average rate of change of
h(x)
over the interval [N, O] is positive. If O > N, what can we determine about
h(x)
over the interval?
h(x) is increasing
400
The values of
A, B, C, R(x) and Q(x)
that make the equation true.
(3x^3+4x^2+11)/(x^2-3x+2)=Ax^2+Bx+C+(R(x))/(Q(x))
What is
A=0; B=3; C=13; R(x)=33x-15; Q(x)=x^2-3x+2?
400
f^-1(x)
when
f(x)=(x+3)^(1/3)
What is
x^3-3?
400
The location of E' on the function
f(x)
given the transformation
1/3f(3x)+1
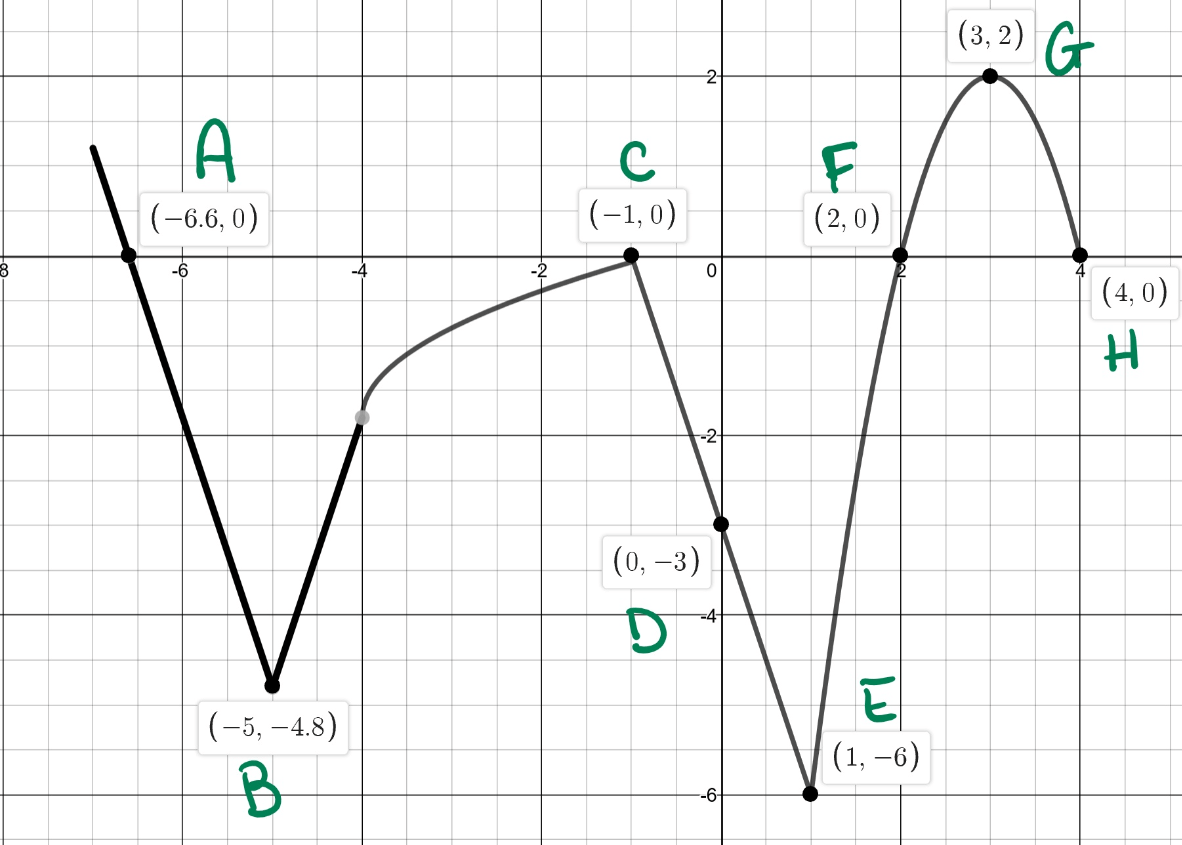
What is
(1/3, -1)
400
f(x)=x^4-6x^2+2
g(x)=x+1
h(x)=x^2
g(x)*h(x)
What is neither?
400
The average rate of change for the function over the interval [0, 2]
f(x)=20x^2
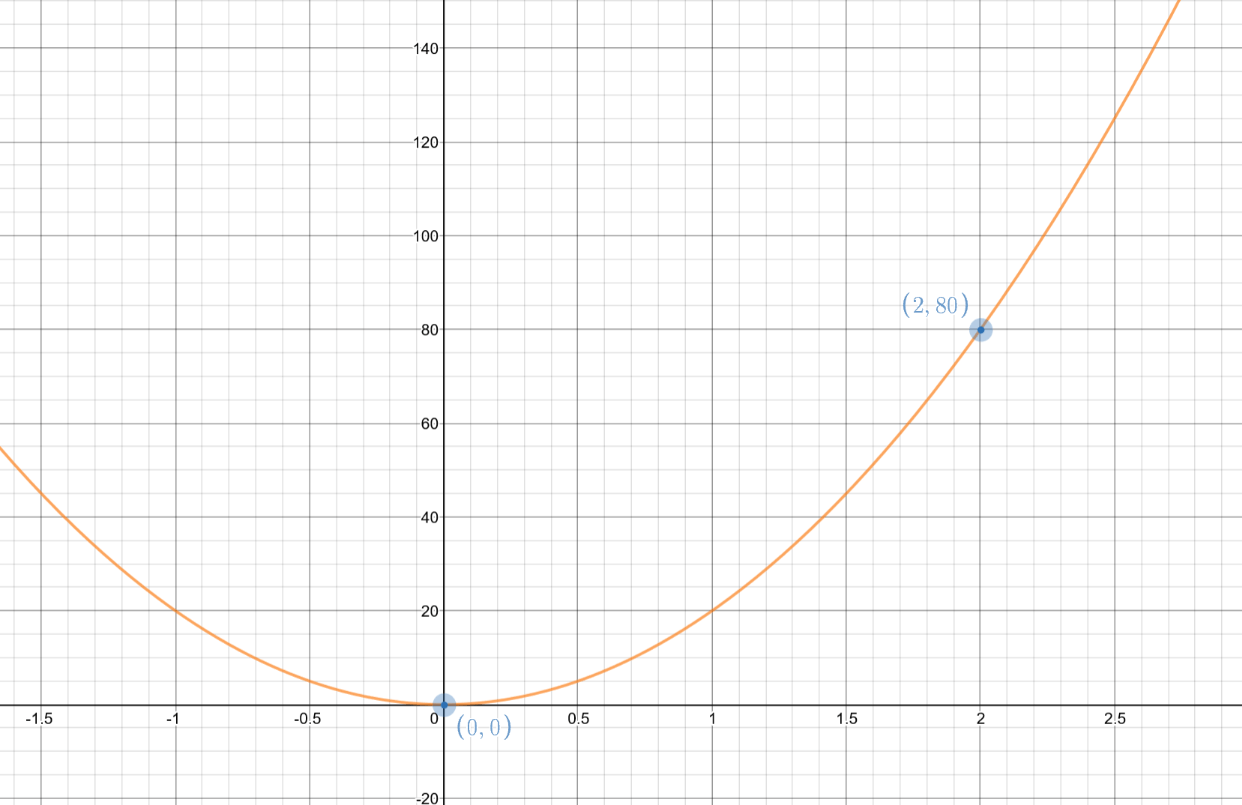
What is 40?
500
The polynomial that represents the area of the base of a rectangular gasoline holding tank at NASA in Houston, TX when the height of the tank is
(x-3)
and the volume is
12x^3-25x^2-38x+15
What is
12x^2+11x-5?
500
The restricted domain and graph that makes
f^-1(x)
invertible when
f(x)=(x-4)^2 +1
x>= 4
500
Given the four functions, write function notation for the transformations of r(x) (red)
b(x) (blue), g(x) (green) and p(x) purple.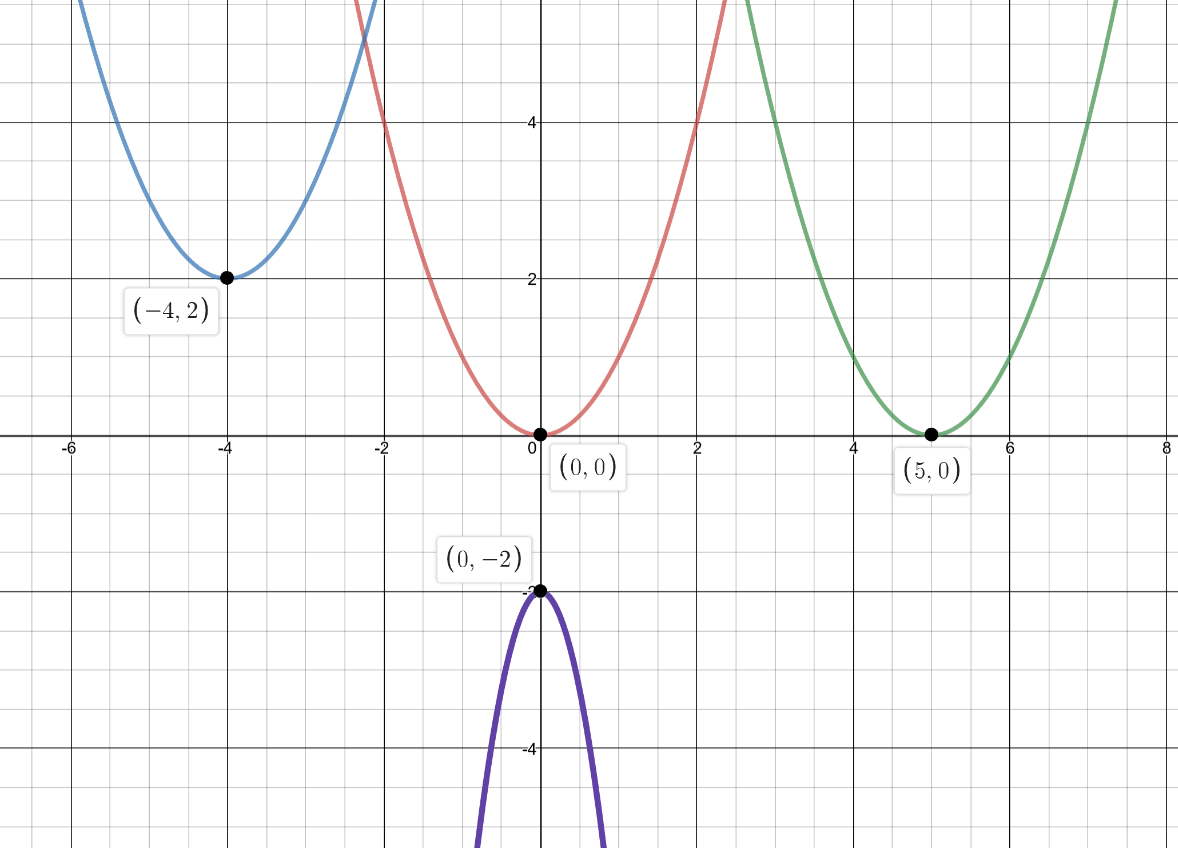
b(x)=r(x+4)+2
p(x)=-5r(x)-2
g(x)=r(x-5)
500
If the point (2-x, b+2) lies on the graph of an odd function,
g,
this is what g(x-2) equals.
What is (-b-2)?
Since plugging in -x for x changes the signs on an odd function you would take the negative of the y-value (b+2).
500
Rachel went skydiving and the graph below describes Rachel's height in meters as a function of time. What was Rachel's average rate of change between 3 and 8 seconds?
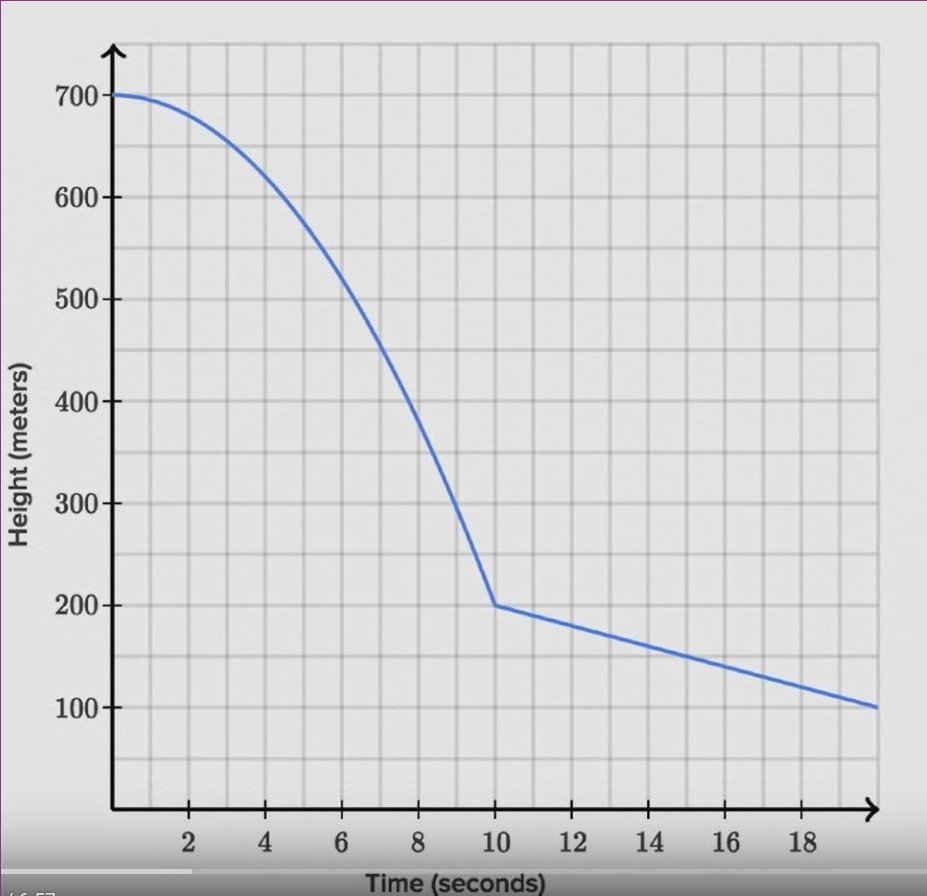
-55 m/s