Linear & Quadratic
Polynomial
Rational
Exponential & Logarithmic
Reading Functions
Combining functions
100
Find the equations of the line with a slope=-2 and contains the point (3, -1)
y=-2x+5
100
Find the end behaviors of f(x)=x4-4x3+9x2-20x+20
as x -> inf., y-> inf.
as x -> -inf., y-> inf
100
State the y-intercept of (x+2)/[x(x+2)].
undefined
100
Expand the logarithm.
log3((uv2)/w)
log3u + 2log3v -log3 w
100
y=f(x). Find f(-2).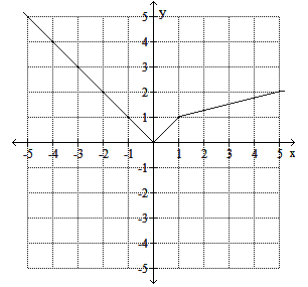
f(-2)=2
100
f(x)=(x^2)-5; f(x-4)
(x^2)-8x+11
200
Write the equation of a line perpendicular to 3x-y=-4 and passes through the point (-2, 4).
y=(-⅓)x+(10/3)
200
Find the end behaviors of f(x)=-4x3+9x2-20x+20
As x -> inf, y -> -inf
As x -> -inf, y -> inf
200
State the excluded values. Determine which are holes or vertical asymptotes. f(x)=(x+2)/[x(x+2)].
excluded values at x=0 (VA) and x=-2 (hole)
200
Condense the logarithm.
3log3x2 + ½ log3sqrt(x)
log3x3
200
Use the graph to determine the function's domain and range.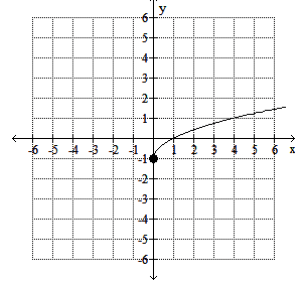
Domain: [0, inf.)
Range: [-1, inf.)
200
f(x) = 3x2 +x+1 and g(x)=3x
Find f-g and state the domain of f-g.
3x2-2x+1
x| all real numbers
300
State open interval in which the y=-x2-3x+4 is decreasing.
x| (-1.5, inf)
300
State the zeros of the polynomial function. f(x)=x2(x-2)(x+4)
x=0 (multiplicity 2)
x=2
x=-4
300
State the equation of the horizontal asymptote. f(x)=(x+2)/[x(x+2)].
BOBO, so y=0
300
Solve. Write your answer in exact form
86+3x=4
-16/9
300
Determine the domain of (x)/(x^2-9)
x cannot equal -3 and 3
300
f(x) = 3x2 +x+1 and g(x)=3x
Find f x g and state the domain.
9x3+3x2+3x
x| all real numbers
400
Write the equation of the parabola that passes through (1, 6) and has a vertex of (-1, 2).
y=(x+1)2+2
400
Find the third degree polynomial function with real coefficients that has zeros at x=3, x=4+i.
f(x)=x3-11x2+41x-51
400
Find the hole of (x2-4)/(x2-x-2).
(2, 4/3)
400
What is the domain on ln(x+7)?
x>-7
400
Use your calculator to approximate the coordinates of the relative minimums y=2x3-5x+1
(.91, -2.04)
400
f(x) = 3x2 +x+1 and g(x)=3x
Find f/g and state the domain.
(3x2 +x+1)/3x
x| x cannot equal 0
500
Algebraically find the vertex of y=-4x2+4x. State if the value is a minimum or a maximum value.
(½, 1)
Max since a>0
500
Find the complex zeros of f(x)=x4-4x3+9x2-20x+20
2 (multiplicity of 2), sqrt(5)i, -sqrt(5)i
500
State the horizontal or slant asymptote of (x2-4)/(x2-x-2).
EATS DC, so y=1
500
log3sqrt(x-2)=2
83
500
Write the equation for the piecewise function.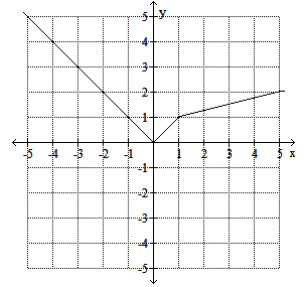 
y= f(x)= -x x<0
x 0<= x <=1
(¼)x +¾ x>1
500
f(x) = 3x2 +x+1 and g(x)=3x
Find f(g(x)). State the domain.
27x2 +3x+1
x| all real numbers