Laws of Exponents
Integer Exponents
Rational Exponents
Exponential Functions
Exponential Growth+Decay
100
The expression to (123) (123) (123) as a single power
=123+3+3
=129
100
Solve: 80
1
100
Solve: 41/2
=√4
=2
100
Complete a table for y=x2 with first and second differences included.
-2 y=(-2)2 y=4
-1 y=(-1)2 y=1 1-4=-3
0 y= 02 y=0 0-1=-1 1-(-3)=2
1 y= 12 y=1 1-0=1 1-(-1)=0
2 y= 22 y=4 4-1=3 3-1=2
100
Is the equation P(n)=P0(1+r)n exponential growth or decay?
Exponential growth
200
The expression 616 ÷611 as a single power
= 616-11
=65
200
Solve: 35/35
1
200
Solve: 322/5
=(5√32)2
=22
=4
200
Create a table of values for y=2x with first differences and constant ratios
-2 y=2-2 =1/22 =1/4
-1 y=2-1 =1/21 =1/2 1/2-1/4=1/4 1/2 ÷1/4=2
0 y=20 =1 1-1/2=1 1÷1/2=2
1 y=21 =2 2-1=1 2 ÷ 1=2
2 y=22 =4 4-2=2 4 ÷2=2
200
In the algebraic model P(n)=3000(1.15)7 identify the initial amount, the growth rate and the number of growth periods
Initial amount: 3000
Growth rate: 0.15 (or15%) 1.15-1
Number of growth periods: 7
300
The solution to (72)3
=(7)2✕3
=76
=117649
300
Solve: 2-3
=1/23
=1/8
300
Solve: 27-2/3
=1/272/3
=1/(∛27)2
=1/(3)2
=1/9
300
What type of relation is this and why?
This is an exponential relation because the constant ratios are the same
300
An ant colony triples in numbers every month. Currently, there are 12 000 ants in the nest. The equation for this model is P(n)=12000 (3)n. Use the equation to predict the size of the ant colony in 3 months.
P(3)=12000 (3)
P(3) =324000
Therefore the ant colony will have 324000 ants in three months
400
Simplify (54)2(55)2/52(513)
=58 510/515
=518/515
=53
400
Solve: (2/32)2
=22/34
=4/81
400
Simplify: (109/4)(10-2/1)
=(109/4)(10-8/4)
= 101/4
400
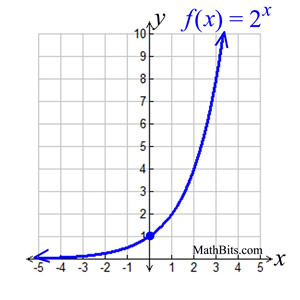
Using the graph state the domain, the range, the y intercept, the constant ratio, the horizontal asymptote and if it's increasing or decreasing.
Domain: {xer}
Range: {yer|y>0}
Y intercept: y=1
Constant ratio: =2
Horizantal asymptote: y=0
Increasing
400
In the algebraic model P(n)=4000(1-0.27)13 identify the initial amount, the decay rate and the number of decay periods
Initial amount: 4000
Decay rate: 0.27
Number of decay periods: 13
500
Evaluate: 52[(54)3/510]
=52(512/510)
=52(52)
=54
=625
500
Solve: (4/7)2 x (7/4)-3
=(4/7)2 x (4/7)3
= (4/7)5
= 1024/16807
500
Solve: 42/3 ÷ 4-1/2 x 45/6
44/6 ÷ 4-3/6 x 45/6
= 412/6
= 42
= 16
500
Create a table of values for y=(1/2)x including first differences and constant ratios
-2 y=(1/2)-2 =2/12 =2
-1 y=(1/2)-1 =2/11 =1 2-4=-2 2÷4= 1/2
0 y=(1/2)0 =1 1-2=-1 1÷2=1/2
1 y=(1/2)1 =1/2 1/2-1 =-1/2 1/2÷1 =1/2
2 y=(1/2)2 =1/4 1/4-1/2 =-1/4 1/4÷1/2 =1/2
500
The value of Mrs. Hookers Kia Rio after it was purchased depreciated according to the formula P(n)=25000(0.85)n where P(n) is the cars value in the nth year after it was purchased. After how many years will the Kia be half of the original purchase price? *hint use log
12 500=25000(0.85)n
12500/25000= 25000(0.85)n/25000
0.5=0.85n
log(0.5)/log(0.85)
n= 4.27 years