Which equation does not represent a linear function?
A) y = 2(x − 3)
B) y = 22 − 3x
C) y = (x+1)/5
D) y = 2x2 + 3x
D) y = 2x2 + 3x
During an experiment, the temperature of a substance increases at a constant rate of three degree Celsius ( C) per hour.
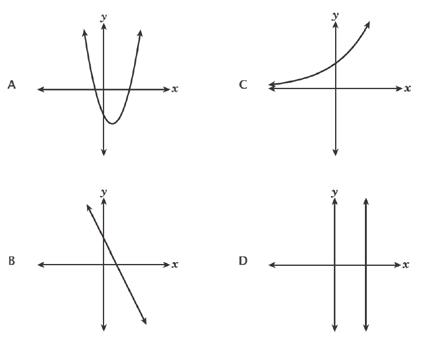
Which graph represents this relationship?
<img data-fr-image-pasted="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAdQAAAGlCAYAAABDWQcIAAAgAElEQVR4Aey9D2xbV5ov9put05Ktpo9s7YJ8tQvzrV2Yqr3P5IsHIRtPYS48rel6FqbgKSwh2TpMsk3kZF8ibdqJ9YwHj+xBPZIHcKQEmEQJGkMKMIZkdA3TwBpDA/WCDOCANJBANJ6NoVsbIPssLC82eqtbjPapv+9cUqIoSiIlkley7zEskveee/5893znO9//H8yxwCoWBCwIWBCwIGBBwILAuiDwR+t62nrYgoAFAQsCFgQsCFgQUBCwCKq1ECwIWBCwIGBBwIJAAyBgEdQGANFqwoKABQELAhYELAhYBNVaAxYELAhYELAgYEGgARCwCGoDgGg1YUHAgoAFAQsCFgQsgmqtAQsCFgQsCFgQsCDQAAhYBLUBQLSasCBgQcCCgAUBCwIWQbXWgAUBCwIWBCwIWBBoAAS2NKANq4lmQEDXoU3rsNkcsLUVO5jlJ6/rW2y8XtapXJvltfl6OusBGq9D6sr/0r2yx1RbRlU4HEaDOvvU+Zw8Uyr6bMU45IbUQ5V2OUZ9WgNk3AtNAHJd2m0rv1jsQcZfGofcl1Wp2uFFFtU/+5IGq85D1bL+WBDYABDgutU0zcAfrmVbaYeVNV6OozJU1lU4WMLnIo7Mr/eV8Haaj7Lt1fBW8NBRjvsch8Z+HFXwUHCfSLYEx+T68nhr7AOqveJcdc5f2pF5KFzm99I4eePZLhIpySobCAKF38/97jf9c53HQnOBFwNzoRPdc0Pxghpg4e5nc9H9vrnuy4k544pcLswlLkfnXIc654bSM6re7788Mxfe75nz7Q+wDd9c6Fh0rv/LxFzOuD039wc+MzYw130irO4HDnfPDUz8fm7m8e/mzpwIGM+xH99e/udngP9Dp/rnEjnV/Fwu1j8X2sv2D52Zv2bcmZv7/W/PzEXYt/dI/1zqaelqYW78XOec5/iZuRuPS9f4ybne+HxgrueVyFxIxnk4PBe9fIPjnJlLXOicC+z1qrGEXuKY9gTmui/yXtnj1lcLAhsHAjNzv4+Pzp05JWuZePdSeO7Mx78rrtffzw2cID6/PDCXWkDcuULys7lOweePU3OCmoW/GSCuGWte4dzh6NyZz9nG98VZEm9TE0NzPScjBk4S5wcmJudmcom5Hmm/iKvzeEuc8h3vn/tdtvj808Rc/yHvnGcvx0Z8X1Ryv5vreck3590fnhv4mwUsK8QH5joPhef6/7qs/ve5ud99WcRbPhM4HJmL/nxczTV3h3Pa5WU7vE68VfvPYY7hcWnzWdTrM/ejdH56tk8Nm2Z2OpJXBtF7KQ7P8SiiJ9ywz84A9uIEeLqcIfc3Mz0j/Fqx2Pi7AL2gDrvqmnCIBc0Gz4kudO2zIXV9BCNn+zFjG0L/CQ+yVwfQdy4GHAjj9PtdmJmagV0adHjQ8Uov2nkizd0ZxcitLLzHu9mGE3B54VInXQ3xmwm2P0MOOo4b6TwCR1ylwahTtzaVQy5/A6O3IvCd9Br3Zjimp3JyLRYtg+EPT2Pw5gx8h0Lo5Dic01lkyIXOyDy/18hhOxB6+zRCLg6Op2rbbi8cpeetTwsCGwgC+r0J9H3Qj6wzhI63O+DWibdcrApPhVMjzmpTRNLyHZc4Idxcgetd6mnTOa55wH24C90B4u3NMUx8eJ6NuNFPPMrfGkbfh+PQ94UR/bAL9ic5xU3qNuLtqR4EpzTkvh1H/5Us/Me7ED3kZn9etBeRJn83jnhW9pAs0rfTyB/3oAxzlWQp91BD7MoNRA5H4SnCV3tawIxw01L47MgHpzF8PcdxhhF5swtu5JCdKuLoH3Tkn+jG3nPcCxvngy1utG9VkFBNPMt/yl/vszzPzTE3LtZ4MoHs7i6MnOuBr1xUIzOgCEjWp4iR1KeaFb/JW+T/efGS+u2An4gZOexAeB+QDpxHlsRPP+FE+mYSOc2PoYv9JFaqkfk/vmMe+PgrO5vAeFKH91AHIuUE8yGR8jtefyUK99dJJK/FoR3pnCd0SlzV5oV3K5DgvTSRylfEJZui2kZXyU/6MXyzgMC7Axh+LzT/vHFXQ4abjIMEPnisE5Fd88OzvlgQ2JAQyNy5gey0A0d/3Y+el5ce+xS+2uwUg5YN/wUiBnHVzv9yX8ivqHM8gnPHXYjssxNne5DMZCmm9WDyDveGNg/6iLedO9UD838CR8Lqe/b6JAavafAcjCDCw/NCySNxMwXs5iF6fwGjyRgS91lnT7GGEH2Kh917OKZ8HGO3OnCGewfU9YVW0lfPY/BqFj7i7eDPw3DJXlNW8rMa5+SCxxdG53HZSZ6vYhklbaT3TWRytZEbfJBA7DpPkNSTLCpc3CXdZpFG8fbCNwMpjSfsZGtLBEx/SkLa5oDdTb0mSZdNnRYnMXE1zpPloh4W/eBZdtFv+ZG5ncBkzoWjkSjChxwofBtH7OFCNYPY88T8ahR+PY7xW3l1U8atxqcQMIPE7Sxsng70vlVJTEttGfUX6X9Kt6xPCwIbDAKOrW6qQzWk/jqG9CMSlYpi2yJiJkqWygnQHwR7KZER6YuqX8RvSmmk6JpwrE64nE44iD9OJ3GC0p/41djyeMu2BGtt5YRbGnuUwvjdHFzHutB5JAjPo0nE76TlTrEIvtngPRJFZD+QuhaDYK7aQ9iWnYcBzOaRuTMJkFhG31pKTI2GOB95jsT5eSwWQd1Ib52im6MnO9HlymCAItDoaxSJXokjX6KUcpKVEyNL6VL5t/KpzCCL2OVe9L5/Gt0fpeB6oxc9RfFr6LVuhAMaRs+9jq5XX8f5T2LIVBBWwzBC+itrVc8gRoKq7fbDt8cD/6EgMJWiCHgBMVV9PmPzBhE55ET8ynjxYGCItZQhBjeKVIG/d3nhMfaOsk7kKy/KxjOdwciHvRSl9eL0u4OIfb10o6p40PppQcAUCHgoDYoe8SD9SQ+ilN6c/sUIko/KsFRUNzzkLsKnFwR79QUOlUSTVBSTn/YpvI1eTMBxpAe9JwNqTr4T3YiQ6YtfOM0Daxf6PppAZn5zKE2b7fGrtFteMrcmkCVxDh70wbOP+LubHOttSpDmD+2sL7j+Qw/CkRBA0fH4N2xF8JCHgRkZP0XSk3fJ/W4l3lICtVxx2jRKp/qItzKPXpy/llaGUMvVf5auWwR1g71N16EodSDUX34YgS0bw8BZLsyPkvPosRKHqhCiOB91Hi4SXyW2of5GWf3yvm1vGP2XxzF6IYr22RSGSLQGLwvCLQCjxFGWn6j17xJIZSjuJVJ6KY527A0i3KZjkojJy6qU6tuo9wkeC8OvJTB6J8u9xKHmoO5TnCsEs3Q4WOi19E1O6sZ90cdmn2SRo74oV6AOyioWBDYiBLb60H1uCONfUo3ipp3B5T70XBhGWg6qXMs2IaaVHCpvCZ4tcKjqKMmFb6x/RRZJYAvK+paVd4Yw8PEIPrvUjSAPzGPneGD+mNxq2TmTcqkidEqf/DlLVdLNLKVUPoREpEuCGDzsQ5bqpRTVN0Yx6uuzdnheDCHstSH+2xhyM8JDi1haDgNG3dJn8cHFH3Io4Ex12kBkFN5mib/PD95aBHXxctgQvxy7Aoi804/Rq5+ha7uIkW6ok6TDRnHwFi5WIlwJDYzFa/xyFEVFMokZmhscPXUGA5eGMEIEdGaG0X9pgWjatnsRfuMMhr4cQd8xG8ZvjvNELU8aZYFDlZO1FB1piogyj4ggfz2Ijp928JTcjzgJXv4xRdT3DKwuIZvQTNuuMMIH7UiQS03nNDgVkWRTLg/aheJ/m0IiL20vLYaLjRedZwcx8vkoRrlRRQ+X64SWPmNdsSBgKgS20v6AxoQDX46i/12SPIpmx+/IAneScFLcS4JEwcxCmaELC62Q7MRbdZkcokaC1P7KGfRfHMLo5R6486PovTCKTIlo0jgwRAOkgbFhnKFRUeLTUcQfLjQ6M78zLFzT74sxEvWwT+Lo/dlRdFBdMziRgY2GgUkSVaNm8e8M8X0LJWXH/bA9jGH0dkZReeFQbdTfemgQkc2lkb6/0P7ChPiNOlSdxoT+cI/CW8HdoTeo1iHuPw/FIqgb7C3rRDCtKIaxtdnhFEMeioYUZ+eisp8yUhHVpASJiID6Q4pcueg92yiGcS1MRuiViGqkiA+Z8IdZcnlK5EQrYH2+DwfrUT9DYl3iLtUzvCYoY+h++IXIF6dRhL4njBBFvcEDfvgPBIl4Ydh4Es3cyqj6Tj4nxNcoNoR43/1gAqM3iZjqpC53vIicFHFxDIMXx5Auia1kPsVHDU6c43K4qI8R3zi2+5wgZRF41sdmggAXrhBHVbhe3XL45adT1i2xz7uHOlZKa+KU1hhqkTzityjZmSaR2i62DVKEMzW+qZ/EfwNvi8+wjwW8pQeA4BNtLuRzoRR1mPOcKg0Sr8dphOhC4PhRhAJB+H1+hGnEFNylKz2q4qI5VilKMsRP1+EIgq4CYl9RHZTnkUD2EptL4bODBHrk4iiStOZVRUTF86LjYv8cl7i2C94WmzbqPuN/F72KZ3yu65qeruWRmyaiuEiApvLQuNRd4s7R0EJR0RcDmEjm4dhpg3aPHNxTJ8I0w6cEhqucBIyIkL4cQ9+7OQSJpNr9BBLTPLV2HiUCFAcjJ2ESwBuf9qNwC8h9l0JyyoPOV0PwUFSb+WIYg7cnIYYU2qM0Ehk7nyeh3LUwGY1+OOLQXdojsrfHceO2Dt/Z0+h/LzCPrjpPvTN3X8fI34yi850APOx7hg/pPH1Lse0JIkTOcvSXdNMhgylO5VK8J7vR97iA/msD6L1/A95dbp5iNWS3URzNE61wulo+TWvn00gR5jIWzyG6AdFy8Hk57RqQsv6uCwKyjp6QvdvqIsZyfVEE695ZImDrannRw9q9EfT+Jk0CwrY1iljvZOA/0YOQj/sFi7+zA8F7Q4idfR352z7FHabuZuF5hXrRgCF5EdFvIZ9F6sp59KXJCRJv0xkHuj44Cg+bEbeZ7q94eCY+aA/TSH1bQOjVbkOMWxoNRcS6tqDeEYvd8RgNHD1dGD57BsXhsHYe3heyiJ4bxY07dG8LEF/LxcvkUjuO+DFxndbAUzQ+FDcgFg+Nlvrfz6P/y0H0vUb3Pu5Bsg1q3IN6LkeV/hY6DacmiNdPOS8eAmxtfnS8yz6eA9eZ/+BfsyhIWX+Wh4Cex99c7MO/7P8/8cO9/wzZz/53/B//xkYF/+55wrL8w/Xd2fKP03jyfz+gL9f3JEZ/iujp/xV/0UF/LtXMFuw48GME9+/AD77P48Gjp/hh+1FE//Iv0d2xb34s01OPMcWoLLMifvmHWdj/q/8W0d4e/Pmf7UMbZRL/+O+mUfh/n1DH8RQvbP8RfvZmN/7lqR/DUSav+MHf5fH4H2jEEApj3z+dRf67b3EX7fiLNzux+z9bmNOW/9QN539UQPbvnfiv//mfoP0/ISdMH9gf/Q8/we7/gue1P2qD+z934oW/I2LtD+LPDvrh/o/5/H+4jS45R/ETvwdt/34a+UePud1tw58EfoLgf7MNW9h/fnYWW/79LLS/0zD9d/+IH/7xbvz4X3gsRnUB/Na3lSBAYpq/M4K/eK0Pd/7Rgx3/wIPoL9P4Z38axA5Zg40ss/8I/d/m8PjfPMbTLTvwZ6//Jf7i9Q7sKxrv2Fz78ONAO3b8E+DxpOgzvfjx/9yNf336f1LEUoby/30/ham/fwFtVNgoUfA/9ePP3+/DX5wwDpGz/07DLFUsDydzPFz/COH/5TT+tz//Ccrp1A9Y54Hg35/+KX4kp+cnGfxfj6bxo5NR/My3rWzGbdj2T17AD8jyzv7xn+DHf7wNuUdT2HbgJ/jJPzfqtf2X2/DCH7Zgts2N//5/PArvP+UutMWJ3Qd/gqMvcb/5Iw1T/89j5PQfoj3w3yH4L3agjb61j//tNIRBn6Zf7PTfT/NQvoOH6h9hW6NhXjabjfL1BxKqYqMMZqOOQ5cT51cTiNGUvPBiBCEuFvuu4HPpZ7VR35E1LgsCSyBAjiv9Hd26Lo/gxhMvXbS8SDxyo/e95Vw+lrRgXbAgUBcEyniSup57rirbGGAg/Bb9Lg+6kLk6gSSdrEOHfM8VDKzJWhDYdBCgL6SPB+DuV0JwFxKM7pNH8ERoSTCCTTcva8AbFgIWQa351dBybX87jQ1s8L0UhKhSrWJBwILAxoeAg8Zz7m008NlJt5HthvJk44/aGuFmhIAl8q3hrWX/lr5eNi+chSRST1yMm7lcdJ8aGrOqWBCwINASCGj3ia+PGcpvR4EWtRra6Rcd2GkR1JYA/zntxOJQV3vxDLeVTU7gPP0hxZr2KEVGa2JOxbpVDOnEL0S+l/8uH4PcL9Xj53wpPSOf1Urpfvk9Xpvvr/y6fC/WV/dVfxUV5H5pHBW3lvyUuuWlvN/yfsrrlX+veLb8pwpKUW18pUo0PJkfJ7+qeZXuWZ/PNQT0xymM/LoPg9c1BotfBzGtdT2X6lWuQ1nrK633yvvyu7gPVH2u7P4S/C62teR6tZUgdStKaT+o3B/mx1HlGdVE5XWBgaCmfFYr5eOshFe1+pvkmsWh1vKi6LcpvqE2B03i13TA1al7HcTpizfYiBHGS2Ltgs7eMy+44T/Zh4EjOgbf78GNx7xTcmaye9DNwAyRvfQX+4hhvH4Tp0tbCN2/7EP0Zdf8yLPX2fbZUQbndqPrwwGcOeWFdvM8or+6wUgnbO+H9INj9JPQT5kd4iWass8ypN+bfRhJZ2FnnFD8gePQ6cz9bj/OvOJB8hevY2AihRwna7czluguHw8SXQgfrsz2oiH5625EP84j9Bqd0X/Ow8Z0Guff72cWmhwd1jlEIo4Y3MucZraF0HepF547/ej7IofwxWFEXyweT+jmM8jsM3S+wejFKCMxMavFz17HWJZj47NOpxue/SFEGHIttEeeyWPig24M38nxPv116atb+N6m5tDzCt0S5qFjfXluIcDdXKxlda5jlzhFrqXcj6H3HA/TEuxLrWSuY65HO4mAI9CF/nNdyHJND16bxIyDuPYC1+v3tI6PEKd/HoB2exi9vxhmqE3i4GsMUkLXsvmRPIrjPLPJjKYLcB/qZQSkTnimkzjfyX3gew6WuOfZKVGNOuguFlB+nZmrxP2LceKW4WMOCQl4uBejZyNwfDeGrvdHiPPMHkVrXNs2Ris7EqHxZLgiVCDxlskpei7Q7YU4P1g00kp/ehp9dMvRuR9IETceiZDETQuhD4bQvTuDvleGoTMc4tC50Pw80p/Qle6ajg7uVZ27cozgdBpDtwrGPiZ4y4hqkU7aoOwn3tLzYOLXvegfm6SPrhHXSeIotb86wAAQmx9vS1u3wM8qy0GAvmXrC9JOB+/dPnS+RiKoM8bubycQ15zofi0CNxHd46PT93QCuQeMZuJkJJMTRB453jHtkdwXLi2fY4SifIFBFBh/824XNBJURYro0pNOMtAD/dfEuTqb19QsCoyXm32ch5OhDDu9QHKCiM20a7mP6Mv2MskRIx7lp9z0TSWy0fla1+3wSpo29juTyyHzUEfwvSh82xhC7Po4et5NI3dpBD3lmWfyDLg9kUSB6d/id2JIURQe4qEjcKQDjn30Y83GMfBVmpkvmDHmsJFKSiz5JcB3VubKKc4XIlohz34pEVCX+Tv/gOEGSei76MPmYHSWOA8Or3+dw2cS3m07Y8IwoIS46ERe64TXwad0+gl7G+9jOD9G68vmggAJqWOdvuI6XUZCzKbkoR+0pDQcS2rwHSNx2E283OlnwIMC0gyYMvkI6PiAvpYuLkPGzHXv4RcWCXCfy9KtTFIsEv8yrwTmfUGzd5NIJFMMLWhDQYKuqAcKyGXo5749gCiDnxSIVyMfdtMXdIDEmP7ZU1zzUzr8x0hk6VQqYQklJrYi0oy1myFeOQ50MgC+G5KubfxsL/cGYLg8M0yePuoqqATbusm9gwQ3vIv+uV4eWE/S2JKH24kxHtBt9GTgIdzDg4LbQ8JKq+nsQ+4z7F/GqvrkN8HnDHFVRYHiXlWQQC/E2+irEXh5eJ+YoI+uhB+9OoSwi/W5l6W5TUUjEQTk/Qjhfkbw1iKosohrLVxFKiSfin5S60NGPdd+ZmjYz++MqykLPTEVRMcb3fPIhYeyPEnUXgyj663IojyFQlAloqYnEEKQCQYzd5nGaZqISeKEqUkk7gmCdcGRTs1HWrEz4oqtjdFRjpGDPOZAB0+HXT8bZPhAnkBfcqnoQw4Giuh6pxveRauAC56/HRL3k6fKzj0MMLGXTubhEaSSkzyd8lljShSFk7gz2VvXG25kGAlJosCEmDIqxJBoIdbRGAhi5GaOBLUD3Tx9lkqSCCRRoBYViRAj/XITNIr8JoH0EMnfIMfKe34780SeZfjDBxoJKok/77t2MJ7wqShCRX+/RW1aPywIFCGg5RkshVG35hdvjZCxbfchTImHlMyWNGJMpeaXXMXMtGSUvPpwOhh9iEEawjuLl0sfKsJQO7oYOD/FUJsS4cz3oqxxconEJ/g6cJRpGydLOCh4ILi+jwTzDe4DrzCi2M+iGBtLInOS4QCFM3WQ8/xZNzpflroLRY7SgvNu4ltU8I0EeWYqSikOD8OSHaaII7L/pHNu7j9CsIm3yQwJKvMdvxyh5IuNTCWRZ3q3bJvsD8S9Yjf6PYYfFPzkWBd6lt88uEiWLCkyfuK3m8kxOoi3AYLJ79AQvcwgNRkN4aJRmMNDeDG4y7OWmtHSoRrLoKa/WXJ1I1dGmChYlu4aCzkvKbqIarjwSmU+Bq4QldLFsk91n7E0fQcpdn2cYVBro51smog260Iw4IWb7ZXamSERlqIz9q8Uh5unZh4ECjPFQNXSNxd/ebhBVbF49pSnHKWDg5w6OS4n25gvPBgkmWJuZhuRjpy2bxt/30kyj+p8DeNLcRwLV3k4kM2D9RaQUn5Llgxyyvw0rhvjJgqrGMCcCWYYfUkjcGxMYyW/pchfpxwsrGJBYDkIcK31XxygT2p6uRp1XDfEoQsPGL/VOqyCuCpLyywPhr4Agk5GQiulTHsixFWD+wATTTD0YClxRWldG4do9kLXH7cQKyYoB9tRYQsFf+YPngsjkW8Kf/iMUXg4Jgfr3FqmqqIEKMEQojnibfdrTLHoZlSjW3JALz5S+iji4SIdKA8HpWw5BvZJ5SIeSn2F1wt3KKwyCqMsSdB9t+At60mRv/PDVFeejT8CAqvUCIF0Oo3hy8PwUq8ROiI82FqKQS4kRu7C0uPiEuLGW7lvYuj/ZZbhtGXBySkvoPzmFAnhomwP+MgNMotFhtFSXiLneI9c41aG99vnxqgiksZiFQ5VFq/2cBLpryeRYsDuuO5GlDF4bRRTSZxffSqO4V/wNCkjkaDbx0RkVRwfs1mMXjqPDCW1WXK+7lPd6DpWitjEwTFk4Tj1pO7OEFO5uZGjbnaEMUPT9yke21sGFxnHolLaFCqusx7RTsHBgItB7PUcxca/ZNjB2RwS3wHhD3twdE/xWVm9TyU84SC8BJgkYQ6fDMO3s6LtRf1bP543CGTuM/8ug8B7vUx2/6JvzdM31iU5xCJRMBrib65Dm9glXDiPBImG5B4OMESfhPJUOkg5PG73I7g3hmFypXkJ3ZmhpOWpA5GDQdgfx3hsLK1ZfkoCDIpvU3IASI4zFClDFJ7soR7Uhpzgk6Q//JyJvm/zO4mslzrW8IsuDoecIseSvTWIYcYI1h5kyGWG0PNGWGWHUuMlIY+J1OgYJVx7vCgwDePolRiSD7too1Acg9pHOA9pUXCsVGQexd/FmrxjfJP9yyD2/M2NTP+Wfr805PTaibdJHSGOv4OSLoGV4mhzFAVf5P6yTZ53ULLV9UzgbTm4SmCzPqtAQKzfEhS1CnImv0kylBYJ6lqgVzqhSfaGsn4UZ8n2NFompu+Q4LGejcQtSJ2Li5wiUYzXuFaZJSa4HRgQsS8NmZLJPANZ+6kHJYGVInX4oc7N5IbjzIk6KXpYxgKLnO1B5yFBPOpzpAaRNn2HScb5S2MgbE/A0AEJ0ujkQLP3eO/WJE+vfpy+TCvJorhGuknfokiIpLjrkJe/bPAz6Hb7J+M8gSdpRGXkb5R6izcfuWBwoCVOWq6owvku4VAFHoxSlb7NeWRS0HZGMXScjvkyQeHw1X3qb77hOGUTmmWuRwbu9+2UOVrFgoABgdhNrtWH3MAZlKXjBPX786zTWiFUjrnSBn8zV/DkPXJ+IhFiWEHbXhrq7XIZeUS5ToVo+Bh2c4YcauphHrZ7GRS2tcO/x6HSJpbjg9hrZO9S73hqnOucaqAjVNu8FjSIpeAJ/2fTNFB8QnUM9a/6LtoukKAaeMtwo5RgxRiIP5PW4H1jgDhqxAqWUWSopknMuknI/fzF/eUwk41fH8H47TQTiy8YTImES2ZZ4kjlWSnyWxFPfjegwPmq/YKfUuQ5ORxT15v5mnGAHxBvt3Zh4GIRbyUmsNQnXk9+k0BBGqGtiCNw9JnAW/WqFSCsPytCIPMdFykDRXuY8eVG7AY6T5AT4+mu7iInTJZqHKpkkvAe6mYO1A4m3hYiKmJX/lGLm88JEWHUpuBBD+y/oe7jeh6p7x38Tf3HFjFqkMVttM9zM7/zpHyiF1HWd+9mNpqdRYOdohzH5grjzOd98KtFzTNyUXRqIA1FuecG0NGWRt9b/UjcojiXQe5VQnBuHgkG19doACXJjjM2WjZO5ykWziKRnmQGjcDCibg4HhmOUdgZ9UCC/FoxgH7pzgzH5Zzf7Dh//nYxqHf/l1E4bg/h9DmmoaLOJ0QJgcBPHndRx9p9qZ+6GQPZ179ZlkZjfT4LEJA1KiJOOWhmeChL3U0Zh+F1Ta5IPEptED9BTvD0hX7qBGlOKPhaXMclDlUkQu59AfhfGGTAeSaD+JbSnT08wG51UmWzgLfSpE4i6dlHfeZbIXjdxDnuM3Im5h35Q2tiEsQPPkPfIVryClnjXiG3NdWOC96fnsEI7W1Ml0IAACAASURBVBrGmS91mEZHcRoeRoQ7pEFk+jaJGI2Lkp9Q4nSFHDSNGsVgChT7Zk4tGEyJhEt6K3Gk0q8QQuGANT6vhqMuknh+z/nOFsXK8pzg8b4wemj97M+MoOvsDRJs6mn30IqXcGAFgIeAKOHVxQNFObxUk5v4j6VDrfHlxcmRFZjFQRBDLN3i5OzWVGTRs4gOdWFRym/juhAbyWhjIwY5DCwy6qu/5C1JdF2HeNpDHIPMk5h9wY/QfmNRcvkr4itVlQ6Vi9tNQ6bQYRK4EjFV7Ug9fuHJUPQrDvnPvgzkKY6Pt93bPRBjKrHQTdwaZ87T4j1yrjEaBrkOEOHZrsNF03iKj/w+D3KEU6Ko31Vdlealfhh/3LvkIELieyfFAPjGtSw57nSGot3ttGwuHiLUfDgHFw8x3iNHEditYZQxlTOaPEPXAP6VEbmpg5INTOYhSG8VCwIlCAieZihelZyjYvQ3cW2idKvuTwNfeahdhLnyW/DXWKcKb0VnWVyHSoeq7vMpF3GVLnCJj89jOENjHUpTZAWrFubxRCQtRt0I1Uq+/SViKr2QWCnJDHF1G9Ojcc1Lf2pqcpvFIE7k+KjC6aA0x6kxJ+uttEGKHyWZn1WDhwZDoqZxE28ddIkLeomPD0h4S3grY+d4ZL7lHKrNJanmNOQeMg3do+J+RQOm5Dc0tORe4hHRUWkesvcQb11UI4WoNkozLyoZ5vkirTt5vxJe8xU26Rdr+6nhxeWf5BFjku/yzTrJnKRrEh9xoQknJlhUXJJqBOqMOUvz+uQN9P+Cp1cRYZJshl6hpZyLVbhQC3xOcZ60PAy6bYh9TYvDkySWfIuy+GemuWKJjNKuIjb8rRfTLqlO5v+wBtvTHtEk/4IOt1SeoZ/cTzoQeZlEiSdQfZom+cqvheJcEvDgr4cRm4jTbzSExARFaBp9ZOkb2y3+sIo4k0RePY/su0MYiyXQ9VKYjXIO7Eo5i8/3zQNBIIwOH3MqXqUvnJZGO8XVk1/zhOwI4Ex4IXCGzEenVbMaBu8dpf544gJPu3c66bpApanMgSLyoZLuiiyr9yedCL/sUfAo69L6+jxCgOsyRd1pju5mbnKCkoJMfovaxssDYL1FcEmhboloqAbEr5yLnCLWkUt9SBOZdPpDew7Q//MYJUmsUxAOUHBEiX19KHySgP0gXUZULrU8cU2Mdgy8lVq6uNiImw6/L5aBCRli+09IxD4fwOAdti7PkdvroaudIoAyFNkHWBw88IYOjGLgt+NIn+B8b/KTaproe/Q3P7yAt3nqXLveHcboGPGblr7cAZT0RxlKlVOIrT50vBlB7ALzGL/Pg8EBWl9Q9Bx/AITe7kJwKx/kgV9X+45x+Bfxd/hYO8bpOzt6K0uJmUCEm98jutzRRiO3g2JrAtX1UieilIBt9lIOrs0+l6aNXwwaUkRCp8M4FWIKGKf4N/p2BoGXy/SFNY2AyLaHybmZi7Q8r6c4n3uph8w8oq+X6GqJpDaGO/QeI4ZQd+nwUHdK9BKkETQLHQshzHRqwcPtBiLZHGhnzFKpq+pQNCwJwMWHbEmhKNi11w8fxcRZ6jFyXAUag0I4KKYhuaN42Mf8iOT8iiJgl49c6qkEYpJPkj5meSKlV/pXhhB8pLiKPIfoz3aCCc+JUDkilnsbrZIPcA6VOk2HTwWs8BKGMUmW/oSWjC9H8dnPOniCF3SWIpsSRWR0AyjByUffu3CaVtZ0gdDoN+va54eXBhr6ffYpm5rOZ700zTcasP4+5xBIf5PGBPWngrfiCibi1yz9PUV1sxaC6tjeDp/PDo8ypFkArttLfHkxTQNAqmHucx1S/Flw0odT8JXiWX/AD5dYGbK4fRR1HqIP9sEQ/KRpUjyCi1PFdb7FqfYBG0XHxUeMSuovcZtcYsjnhc5cwYkpEa9qFAf7VJ5hF/sy8K2IQ8QzSSQ+eVXDJHWZ9pwTIfYbYZIPVYp46zpI/D5ItxbxmeXwHdwfPHt9CNCrwNhvSkNgHPNTfRil/+3otRvI3M7CtjNAXKbrz+FSUAbiLW0ofNxPlDE+H/UxuESQdiH6Ix4edKqnyCEHd5NrJlGNPWSHws1up1thqZtN/GlFSlrl5clJsYvReeQzyKD4jm00IqD1nDhk+2kxO8ToIBWrbpUWrdsWBCwItAIC53/BKES0bo++HaXOPwH3TlqjU12TKxQUUVUqglYMxOrjuYFA8Yzy3My37omK76mXOr8u+my5yVXGRdR7vAM5RgeJTYwrjs2jdIJ1N209YEHAgkCTICBqGvGjHvp4SBkhZb7N0O+ymzYDTurhR1WQhRBVGVaxINBICFgc6irQ1KnAE8W5lDxFjXLSDdJ3zLWdYhPRXyjR7GLByCpNWrctCFgQaDYEKEkUXWKJC339tdfR/SYjk71k+KGK9a/DysHY7Lfw3LVvcairvPISMS1Vm7fGlQuEnvhcWcWCgAWBDQYBoqWDdgXzRaxjy4pFTMuAYX1tGAQst5l6QEmOVBFQflrFgoAFgU0EARokKT/tTTRka6ibDwIWQa3nnZEjVRyqxdfXAzWrrgUB8yGg/L4taZL5L+LZHoFFUOt5vxaHWg+0rLoWBDYOBCRCj/LQ3jhDskby7EHAIqj1vFOLQ60HWlZdCwIbBwJKh2pxqBvnhTybI7EIaj3v1eJQ64GWVdeCwMaBgKVD3Tjv4hkeiUVQ63i5yiBJLHvp32YVCwIWBDYRBMihLrL63URDt4a6eSBgmdfU8a4kmEOKuUGluHcw7qSEu5svQmSb99vG0ISLY+I2tz8j/JOEPyz125r+FDhLrkgthG9pvr79DKFmHZjmV/Wz8kWynEigfMEhw/WtNetZDuHKupjB85u5P5TWb+l9LeDt/JXm9M/5SXB+vaBjkrmXJeC+0ylBE1s3X5nrevLcliDUiE+LoNYBRXlxdrudEViY2URtulw04kKjdKtcQkIImvBbK2hIMdxh8ACd0pvQ/nLjl77kABFkjGEjpVtz5lfZvyRyd+1myjlm02jlfDPfZuHa6mKs5c0fpLuOZf1cVJUsLRLTVw5L8q9V6znNCE2SFcbtlgw0rcGf3FPG6M5mGXe4CftF2Wqx0c83P5XH+G9vMGl5TN2JMqKcx+NpGXzlPWa4X0i0uo2QutEiqGULZLWv9jY7fHslTZm/pVFWtClNJSr2su+WFi7WXC6HVvebfZxF0AROscCDixB3qzyDECCH6vUyUUOLcUhjDHAX07m1Mjyp8xE5RJlvk+cqSQYkHV6KyTxknpETEYZpbT2Mc9wv1GFlAyxba/uo8yXIwlkULanO59dSXYmpJG9Ui8uCeKzFHbM76dsM0auceK3yDEJArHxNeLczTCnY6v1CcrCqvKlNeI2SJCR+i6kXr4xA4iMXmKFGxLsSIznMbFOtnqtMUXBW+hXJg9nFIqj1vAG+uHmxTT3PNaCuWSewjbBIGwC+2prgRlRKDF3bA1atTQMBcmzcdls+XPsL7NIEQi55UxtZREomhHSUhFTE2JADCouzjanx+F24/3ZvOyYzk43stua2zNofKwdoWflWQmSl3zx+qBOYCccQM05+AgplULESTJp0r/VbHyfCTdfiUJv0Qs1uVhGA1nMwM3+QddXqfiXM4uLYxesF//i1cZWlR2PqO0kMYiMhNfBF+rGrjD4iUTJjnxLomtFvNZhaBLUaVJa7ZiKH2nqkNIBgFofa6i1IzdbiUJdb+Zv/uhyWTONQW308pKSlwRxq9I0oxpmu8sbNOE6/fbqojhGJDjlhMhihQEh5BBjWva1dLgJdi0NtLcwb05uJHOpiF53GTKeWVszYhGoZV1PqWBxqU8C6IRqVw5IJOjaDQ209BBrNoaoZFPe/+K0bSsQbIBHNTRUQOBCYt4w3i1M0q9/KN2txqJUQWem3iRyqWScwMzahlV5BU+9ZHGpTwWtq48JJmcahtn7mjeZQZQZikNT3YR9dcvIYvjSsxLxy/eiRo4a/utof5Urri1n7Y+VMLYJaCZGVfpvIoZp1AjOLQ221kEy9dotDXWn1b+57lg51fe+PxLLvbB8ymRSGPhpQboP+fX7lo+7d5y22zd2C9VpdNpIOlSTCKjVDwEQO1dKh1vyW1l7R4lDXDruN/qQclkzjUFt9PGy8DnX4k2Fa+cYwfHkEXvqIS/Hu96KbulWJjqSKSRzqRtKhWgTVWAq1/TWRQ7V0qLW9onXVsjjUdYFvQz9sog7VYcIu20gd6tiVMYx8PkIOtR+BQ4H51yyR40LHwkVjJF6mNbMZHKoMSCR4G0E9ZYl855dHDV9M5FDN0hFshEVaw5tpTBWLQ20MHDdiK5YOdU1vRXxPhz4egoQUlEhIlUWI6nwRombC4UH6N2t/nJ978YtJ068cRmt/6/ksdQFZFGha7vYwVNZOxoxl0Z7w+qMs8Ae7CvXn9gbh3V62YEzkUC0dagvWiMWhtgDI6+hC15D5LoNcgZ6PThcDonuU3a5exFudPp8zxGnnDh98u8rwVro0UYfq2KR+qOlv0kpvejR8FN1vda/+4tT+uHq1Rtco6VA3wuH/OSSoOjK3Yxi9mUZulpjZ5kfH+z2I7NIwfqkXg3eA4D46LRNVfSfcJKglhTsvmcihWjrURqNhlfYsDrUKUDbOJf1hHBO/jSP7pMADrxPtx7px5hU3Yhd6MZxkzFyfG/YtjJt72EGCWoa3MgVLh1rXi8w+zNKitxdieNTzTo/yNV21AUuH+nyGAvccjqL/pJxndEyc7cLI1QTCfyUZRjwI/qwLn/2VoXRfsoBM5FAtHeqSt9H4CxaH2niYllqkODD/JIfckzyxzkYrUTc8Oxlxp44jvW17CN3nIsxrCuSvD6LvkxHED/eyDTd8r3Zh4L0F/V6p2/lPS4c6D4rVvkiYwdPvS/AGB/ov9MMmAK+lWDrUzUhQiZj3M/SFInLSvMvt9sC10wOPq8aXLsi8tbQ6dDheIGFlFhnjadEBrNyO0hnUsQmUelrXJ8e0SFexrsZqf1j6XA0etbdWX00z5isjrGeDr29Gz2ttDemroxi/mUD6QRa5vAbm9IHLxfR8zCkcPNKFrhMB1IS+TINmKGfYgOAp/zsZ7i6rDFJWga/oUFuNtxyS3S77ycp7yiojr/8256oiGNX/pPI17f1ADik2WvQOc6+ch/iqrQnumIU/Zu1TlUAxYYlVDqHG37PUn9wcxchXMWQeF5DN5ymC5UIlQglR9bwYpuK8A4FdtS8A/X4cY3ftCJ8jR7pFsibkEPuyF6+nvfAwc0L3KyGUW+gVGBUkcSehFp3D5SoOXM7bwusq421ea/xvSTRT0DTmHIw3pf1lx08RjiRVj7PfZs6vsn85IcdoDGEQ1cbDs7K/0m/Z7D2e0nstvl7rY+0Q0DIYu9iPka914qcf4YMdzHFLaHPX0aZIXElgU1/1MfF3GD0fdCO0q0bCo2dx41YCOHga3jYgS81p/PMedH3rR3sggijxdgmBJocavx1HgbFoRXXTqvWsMV+orONslgHlFWFt/nrWp7lfTMt+IXF2a+xPKAHhMnFtTO1x0TejyNKeJPVtqvb9Te0XDKLfyv2Chymdc90oZXMQ1Nk84h/1Y/BmAd6XwjzRkuC5mSxYRv89ieujDFLJOPreTyLyXj+6D9WwKRLZRy6MwnawGx37BZE96Hi7D/6f6Sg8nUT8ixEMbHGi7xWfQgN5YYIYHia+Vv/JFbeq5PJC7EF9RnurulT9FKaZBorUXLJItPJ0n5hOwEs4S0LoVpaEnqJJCzkZqzQEAhJZx+E9ijOdYYT2Vj/o6k/SmLiegZ0bY22cnI7kF8OI5dvR/UFA4Wbo/T54OjUSyyzi1+neMWvHZ29ViH/JtXmIs+3UCbZSfZL6lhlZfmj03RCg1tBIlqJ129P694v+iwPMbcrADZeH4D/gV7jP3a6GHo0qBa3AZ7KEcWv3qUSSh6sNUjYJQWUgrZ0h9FwMwr/HpXQo5fDzIYQw/aHSd5mf74UasizIyZm6gcTWDvS9Qy602Jhjl1gHyo8A7Pdi6M/QolD3wVM8OEuqIjfz/nklO/w8h1o+kuZ8F3FG7qmR5aE5PVRv1cUTZyaTpki9hgNK9SbWdFWyVri3u+GgiK+Vxf3AiYI+g9bOtpUzbG1ftu0+hE/SOIjrt2rh+pI6nW9RQsTvqxcd6SuDGLoFdJztQaj4ohw0QCrhrTOfQPetSWRJUBeRAnKoHg/VQ67WrikbuTzXVpfK0LL6/BpUg7CcIaMhWWFqLRNXJ5BJpyHi3tCRUK2PLaon+Jqh1KGefhc1sMYfwuhYfqj1AM9Gq719bmRvjSMztfTB7K0xDF/Nw3skjPDLi9BoaWXkMXGhD0N37AgeJrJzwWcfaerUmv8ujTTN8jNfTyDOzTXIHH/usr3AcF3hy9OrNNvES8ZiaWIHyzStknzP8+fLVGrGZdlca9pgG9u5JGY2SwfU2JlsnNay14bR+/4wMhRDLi7Ew1/1ofdXSQolWWo42udv0hDpYhz2QBC+LXRxe0gDJ3LB+ftpZO4J3sYQz+jwH/YvJqaqfUoeFBe8eBTN/iXyjla7vMk6lpRqtZb4zRgGLg2gs7MTnSc7a31sST21X9TwHpc8uM4LEkzC0qHWCcQcY0im72hof2vpg/QaRep6AqFTAfjKCODSmrxCsUTB5oZzW46n3QHEic2eA6fR954Hk3fHMXwtTSMlioZoCdx9ckHcq9riYlHIYcqiaTEVLwLP0DVVhWRTL5oyW4oFzYr00lRgmta4huy3OcLUT5yqHASNA212aPQH1ykRWg1tRRdY4GHa7XVgJj2O/iQPwZRaRd/tgjNJgkBLfb3NTWLaib5TVaz0FZFZvZfKUa73t2Sb2ch+qOJrev7CIIIHg5AUbesqan9cVwtreljeqsF0tP79Vg7YBNJQOYTaftspNlo2nBYNlqjgrK0hhxfRc4z8UaV26FQ/iXKVG6VLpZOQCdzTsmKz0tia9CkGO2YUU3q1ONQGv2pa4Tr5JvPV1TB6gbYBtirEr+oobPC+cgafvVLl5qkzGF0Jb+UROSzxX6uL/QX22HLOuLZYvmJ01PteLyS4/cC5gZqkBCvCT+2PK9Zoyk15qxuFQ900oQcdHiccs2mMXs0sfinTGdwgd6rtZBCGZu/CJnKorUdKA8xmbEKLX3ALf1kcaoOBTV34XuqlH8Uwdo0RyMqK9rfjGP06S3pKe4Sy6037KoclEw6HGzUfap7+wL3v98Lhpq8pY/Q2BDTC9JjBbHDRtFqsvtw63TQcqm0XDY8Ox3D+49PoyoRxlIho03NIMOpR/Fsbop8wY/xys2zUdRM5VLNOYGZsQo16XXW3Y3GodYNstQdch7rQcTuFgQuvY/KmD+30Z5mZziOTnETOcxSnj3tXa6Ix93lYErFxq4vBoba6V6GPy+tQdY15TZmKTXuqYfSrUZWKrSEjJCdulg2CWftjJdw2DUEFQ4qF3uJJqm0IY6JE54lXt7ngYbzd7gvd6HqpBedcQsvSoVYuoeb8bv3Wx3lYHGrjX+YWFyIfDsKxewQTt1L0UaSYd5sHvnCULmld8LUAbdWkLB2q8W6JWBL9aPLBJEY+GmmsRa7aHxu/hFZrURgpS4e6GpSq3ScBDb3Rj+DxPCOuFBhxhX6hOykyWmLwUO3hBlwzkUO1dKgNeH+rNWFxqKtBaG3324i31HMGT2i0yuXmR9Gga2vT5UmLx2rpUBU8hj9lXlMGuBCiKvlMG1osHWotxuoNBfnaG6PhUfrqCEZuZ+E50o1uiopWc5BZe2fLPGkih2rpUJd5J428bHGojYSm0dZUBjGKFWMPmHSi8zQ6X3I1vo9aWjRRh1oeba2WoTaiTjUDzgnmNR39coS+pn0IHV6br+mKYzNZh7oR1FObxihJ+yaBeNqNnrPdcKRjmLiZX/HdNuWmiRyqWTqCjbBIm/IuqzVqcajVoLKOa4xqRIPB7JajGLjYhdyX40jeN0WYr8T5z7MOVfKaDlweQFdnV9W8put4yQuPWjpUbBqCmnvKYPhbGAhruxEMq8DwWi0vJnKoZlmxmWXla8q2a3GoDUYpSUTBEKFiPPgNrfMZSrJW77YGD4SuK+K602IxM3s0rHxb3a+4CC24KknQC4mAdPSnHeiWVGzNKibrUJs1rXraJQg2R/H6/PDTgXvkyiTydgcCgbULfDVGVkkwTKFkq/EcYJzR/YstI/L3kkg9sNFJ3IdFkcpM5FAtHWoL1qnFoTYWyAwp5j1I0eKWccSSgI/JK3w7qxAXRjsSveqqxFbLInknjUnmQ3Vu9zPSGfGzrDlN8JbnbE+AYQcXo7RhcGaalW+rj4fiImQUyWsqxDTI6FI979WY13Stq8DSoW4SDpUvSmPOw9CrRE4aNfiOdVQPtk0E1pgxZOUi0VtSJKgpZDMJjFzqYzaM/MIjU0mMnIui41VGUXpUgQgmcqiWDnXhFTXtm8WhNha0U2kMM9tMXPcj+l6U2WQqqBzdZ9LXGZrwQwa7/241vKXA9kkG8XvEW2ZuiV0ZxtAnceS5N6gyzb5o7f/6a32IPazAW6lgog7VDEsVu51RqJih6vS7ktfUhv5zzGvKz6YWk3WoTZ1bjY1vDg51NouEZJgAXWROdcFbfiyViWpEzOQNjF7LwE2DpZ7jFYi7CBgOxvxlgvETxsX4r7pw/q9TdLsJ81TH4NvXUwxNSLP+g+SAVYSTskVY4lAXtdeaH8+dDpXI2fJicaiNBflWD/zMLDHwUS8JoEslPHCVNnWdB1tyTzTWh4cuNL6dK+GsMSwbQw2e+Vdh9UO/PYzTv5xA6gT907czhdv1OHKMgubbaYdTcaIV64eHJTOKGX6odoZ0lGQa4/Q1FShInN568pquHU6WH+rmIKgkcN6DfiQ+HsXpE0x663Yp8ZBdkITZQSRXaI6I2R6mE/kB96rrYSGuKJMdP9Xh2kHdjjz1KI5xxh71HolAu7k4sotqVDhUhayrdtHYCurkV+XU3dhelrZm1nxlJJWHmaWja/wVi0NtLEzp5hagm9tIgHjFHJnpbzPMCMXYvkyL6PAwshlzl3YdCiH0EoO01NJziRizbnaK+NDmYIo//qBUafhOAb7DR+F4skwqL6VDraWTxtYxJ5YvMPLJsPLNFGIqroWtKeZESpK1Y/mh1vmGPS93on9PgJxoEvFkipkmmKCYuhf3Ti/8gXbqVEMI7iehreOIoH1N3c5D5kF9TeKJMiHvNQbYdh9Fx6EC0hWh0mS4BR6nU+x7hnlC3TSOKmVXMLIdyEuVmJJN+KQoW7JqTFyLNaf95cbNfgsm9JtjgvH4bW6MhGVT4LnMfCXvbDvzsFqlsRBw7GUQe/6XRNDKD5XNO0gMFw62dfZHUXL8dga2w90I0Ac9/cUNYHcQoYATE1eEoC4lzzYelmKMqiYJxjWu61atK5UNh+sq+yDTvP2huJ5LUIxdjyH3OIvw8QgK5DQmsi3aN8zYpzjpHBkqBzOSbYRSB/nZAMOlCMl3TP53KgKjRlSLMUOVoevkRoeZCsp2+DQie2zQ7k0gdicL9ykX9DzDohH5CxSb6LNE/CKUnLRY9Hg9SsEv+TrFpUQ41mZ/ShCLDHOzhnmab0V/pfnIZhBn8t5W9yvE1MeA3e6t7pbONyGHJUo8rNIcCNjWQ0RLQ9LziH06ghjzFA9IVpn7Exi+nYfrhBv2aaZilID79AjQZ8n1lu1uOjnUwP4AD9/MfNMivJV+BH/c27hvMIdyc/s1Dp8jX4xg/Pq40p2KERJpHPs1JGvN7Z87E0MaJu6asF/cYix3TtSxqlVbaRE177NsyTWvk2a0vB4Fu/6EhkcXx5ALdKGfiYil6CSectLJXelDShDzMTnCK0xdHoiCGaOMQmjJJu+k+X8p+bUsUinN/BROWBaLzSG9NL+/0nx0mzn9ykYocG71fG3UPVllA0OAwV3inw5hNONmXtRulQxDIwdmI75mrg6g56s8sjx8Zq9MIHSgB76tZXMhh+okYWsl3krvzh/alTFQ8/sFxNd0dGwUXQzpGKJ1tSTeLtGYVuwb6rBvwj5VkmSVvW3Tvm5agrpmiOlZjJ7rw2DSgW7S0gTFI85tfupfujHO/6rcH8PRN3jSertjgZgWOxTi1vJCkY4pfqhm9UsAa9ShUoDfclCblS2j5RPdhB1mr/ajl1Il75u9KNyNIcb8p15fFEN/U0zG+CTGYPsj8L5NI6dyYipzFR0q13Ori9KhtmAdJ79O4vy58zhKPXLnq520hK5iA9LkyQtBNQN/FAfO/aJ0aGjyNFdsflMTVC2fJxfDbbeefZdI5fTRMtBGjpRImZ2l8/luJ7wMiTbfzFYvIp0OtG+fv2IAkc8qa1sTENPyQ11xHTfmpmXl2xg4LtuKjvx3GWSfiv+3j+kYGY3bURL/LPvQwo022jucDFEVw6hp17l57/DBudu34HPq8CDc2UEf1Qq8lRbE4Iz/Wl1akQ81/yiPPop3xVf/zLkzkN9YIdtM02Cg9semtb5sw/JWzfKCqBzUpiSo2ncxDNPiN5V3o+MDGiaA/mlPPYgeqyHYM5Ey8tYZRCohUf57qw/Rt6okPia0FKdoBtSU1Wv5IFvz3YxNqDUzq9KLZeVbBSgNukTdZ/yTIYzcStJVxoueT7tho74t00ZXuBM14C2H4TnWjTPHVhhPmxfh95ZpSw5LC0fmFRpp7C3DyrexbZa3lidT0cM90LXDo3xN5d4M51oeKam8flO/m+yHasb7rYTnpgk9OD9wLYORzycwOUtXF+bzm/meRC5HR+8v4sg0+wBqIodq1glsIyzS+Xff7C8Wh9o0COv3xjGc1OA/FoGPSa3FDgEMnJ+4lYbwU00vPCxxp2h6N5UdNNMPVYyAJGCDBHAYvMgUeVsXuP2V8qFWjrFhv0XsagazwQmYtT9Wwm7TEVT9YYJGQy4cfZc5UH0uJdhw7qCh7WsCTQAAIABJREFU0HQOGqMoNbWYyKGaokMlMM3iUFu/9XGyFofaNPTJ5Zi/eLsPQfqTe2n8JVxUS3Wa0p9JHGoz1DViyzHIKFSZ+xn0XxyAa6er7N0tjuVbdqO5X9X+2NwuqrUuAn6z9sfK8Zh0nqgcRu2/bbT+dG9JM2xgFg6e0GxTWcSZiaZAZF0Ud7f2JmuvaSKH2gykrGXiZnGoVbRgtQx3fXUsDnV98FvhaYmZ7ZP0i5eTKDzIwX2RyS6e6Ai+FaLxWQvKM6ZDHaHr0DgNKgdITH37K9VTIt4WjrzFxdKhmhFlcp0vmUGxw7vjPJ31qeD2+DYOpzuIzrNH4Wn28cBEDtWK5bvOdVPL4xaHWguU1laHtgtHj4Vw4y4JKt2xstMOdL3ThfDhlpBTZeVrxuGwGTrUMeY1HfnNMPrO9iN0hPHNqxRLh1oFKC241GwS1Pgp5LMMYabBF+ll9BXyMQy84D0QhLeaZV+jezeRQzVLR2DGJtTo11ZzexaHWjOo6q2o349j5CqDk5wbQv8lE+QPz4gONc4QjpLXNPpa94p5Tc3hUC0d6uYjqBLcgH4yeRojeen+4mboMUFPjeJfB+81tZjIoZqlI7B0qE1dUc9N47ad7fTpZkzfL4cZnSxInBUdKoMteBjQfs+CMU3TAGKiDtXRoEQP6W/STMV2WiUJ736v6DNfFWDPpw51Ixz+Nx9Bpd+obUsGNz6N0UKQTty0GJT4oJ4Xu9BzMYKmRmI1kUO1dKhVd47GXrQ41MbCs7w1jQSUdDOfHEf/7VF1R5t2IvxmP7yM0d3ko/Cm90OVzDx9H/apCEirJwm3dKjlS6+V3zcfQSXqeQ52oncHncJLHCOJrIMZFVbPM2OANv9NjNkvEsjNMMbmwTC6jnjZKvU6DJ49xriQM8y92s7rkcNyvayU+jMDapYfatmLaNJXS4faJMCyWdo+dL3NwAvKtaKIVTyg2uk+swjHVhoB3WwmrjFlW3YGzh1BRF4Jw0MJVfb2BCZuM+0iE7d5DoTQdcy3tE05LC29ulJvDbnXCB2q5HiWJOESvrDvQm15TS0dakNeX92NmEEa6h7kogcYDSV0gsmKF12s54eOXE6jnJjWwm0a0l8NM3l5D3oOu+l2w7igTg8P0jk6oY+QsFJPe6jMaMJEDtXSodbzjtdY1+JQ1wi4Gh4jIS1Ithni0Lwagd/RRn/UGos+lUNhlnlV3Uy7mI5hMKfTMCeiEmXYfijW/8Tnq8PI287gzOEKWdUm1aFKgoo+hkoVF6N+usmUYgKvBjJLh7oahJpzf/MRVKZuGiGxi6VzcFKXKt5lootx74ugl8mHy8jfMhCzwXekkxlrjNsqwThTQUWJgL5jjAGqrjMw/mtdiH+dgnYoLJIqowiHyn8tt42WCCTSb6tLab6t7tcETkJN0eJQm/amtYc3MHh2BImsJFww/AZtbT76k/ei52QVjrLKSGy7mAZuj3FDY4Lx3l/GkXgSQYTZp7wlfP5lBwaZNUojPs/jrTwiOtQG6TKrDG3ZSwaHWjMPvridIhFN3U1h+NNhlbFmcYVlfsk6NnbGZSo057Ic+q1Yvs2BbRNbtcHJNFBuWvWKyNeh0Q+VBNHu66x9Gy4dI2azYKpCpmRzLyAfHaY1JinOTPPEy5RLi5GS0+IiVym++NmqMqMze7rMroV9ytzkdKz6lY8SzORGk4sYYCnEbPF8ZdOVvJlWaTwEHHs7cOZScH7D1R+nldrF5pA0iDWWsjWYoxh0hs96SkHwS3j7mHG5D5bhc6lpITLfcyG3eE2p+EySUKPefjnXwV8PQnKbSjQk5WtaYxs6UxAqmNZYvwSi9X5qOtVw0kiL+1W7lAmHpWrwKlui1W5vwGsSuP69/rJYvDoy10dUWLN6R5u/NYFxJhiPvus1HpWwhhSrjN1i0AimbRs4XLxebLgwVUCC+Q0lwbjTVdTYim5TXmYTP4W4zFAcPUHkamY/S+bBeRc09nuztf1KUvP4beaqlawHTYRr5XwLtBT3WAnG60Wj2uozAbSn3Jp3rxc6DW1GJZflkcjig+tqLT5hmrKbk3Af74OPOlToGQyfJfG5Mwl9XxeGqsX0Jg7F/zbOPMc8nMqG36J1VWBYQHvephKMV663qr/JWwqnF7slRpdxBA8byq2Ja8RBKTWMW+0XJOKm7Rct3qdkv9gopcEEVbg7RkCZtsPDUFiyHzalyImPZyERg6ouJBn4NxoyVI0GFrGUy/eufzeB/o9S8J/qQ3hncaAOL6LnRnD0ZzEMXUyohOPdTGheKpJgPBgIIhAIGOIXQUyBYJM/s4+Y75GRocKCXC3orzQfiREqyb4jx8It7Vc2jxDhrGKTtnC+kk+y1afr0toy/ZM4lSfuzshabqMKRbI4CbFqVCH3kn0oib8NtYltlnYKTOieo01EXdshc5+OXBpDxnEUA8eLB16bF90XPkMHfV1HPx6jgVKWQfQX8FZNgesodCiEwMvM2dhkfC1vP3knSbsMBzlMjrXGfsXwStZiz/s9iL7B1HQ1Pleql7mfRe5xVs23pfsFpQbCcIRbuV/w5aqDQ6PW6Trbke2qYUWct/tOdmHkkR89H9OB++RiDq8hHeWpQ/14GLHvaEDURkLIjUB7rCmOUiz+aik6s9UMXhyH40QvzlRmuuDp0LU/DP+WUcS5MDUi5jyNFmjxv72UiLoEvSZ/2m1iuJExiJpMsMn9ldpXHKJsdy3qr9SPCrAtfba43+cyli85nuydCYx8NUrxIlUdUzpVHT4EDkUZgCEKT4MOxdp34zgvOtTHJR2q2AUG0XUqUIPdgyx6FhLTMQaBT84GaKDTuXhsXCuuvSF4dwxj+B7jBhNvFw1dxPmlE34L15XYeDjq6DfNvKbDl4YROR4xiKnMu87x2rg/qUNKnc/V209lfYGvKf0SRKImMsOKW15PeSmBvPzamr9nmI4plXfS2o7RjNKMt0ti1fBwgKI/ZaoiD0OXSbFtYX/HAug4wZigtcyGCcaHL/RhJO1GZF+CBk4p2LcHEQ7YkODJMKsTDRloPz3rQeDF9gViKp3xpKhempwYW1lEzLN4e2hN76X5tqY383t57qx8SUzpy3363X6k0I7Q8Sg6aDEkYkqbg5tyA9e5Y9dR9JxrR1TtuHzVPLg6XB54d84fV1d9/5mvzmPg0xQ8JzxIfDGMuFj8H/Awr3Ec6TwxRM8h88CN0MkKYiotiw5V4dGq3TS0Qj35UJWvKcMJevd551OxrWkwso5NiOWriFote/CaJrX8Q2p3FLXbBiiNm/40UzHdzcJ5OAL/dEzpRjKvMdDCngZPlDFBw6+cYYLwcuhxY3iYh76LYqryy9W+c5PwnehGt08jgdSUUZIKqs9TnZMcb+JxDna7G+F36YfKpOOLCqGlkLJxUFvU/Io/TNgMZDymWBevCIgm3lSbbhPb32hN069zjNaj8WnaEdDwZeCNsgALst4auc5J7NKPbSTaTGJRhIP2tzHmR7Wh443Q4oPrMnByesPo/tALqrqJt7QmpL+48CVi7a8/JVdK15ngK1F0HqoQ90p7isisujss0/PaL9fqhyp5TfvO9ik1hxghrRf2Zlj5yiGpkYeweqD+zHGo+v000g/t6LrAZLe3qR9h4IQ4CWx4T4PFvloagx/FVbLhyH4DQbS/HcXw5zq6LnXDt9qBlwRZTuLV/FgDJyVZ+QpFODY5CTXw5L5Cb4tuWX6oi8DRnB/PGYeqPUxh8i4zvwQiDIZQRkwFug078fOw+10amZsjGJiYoX1FFEGPnVZ2Odyg+1u6LYLQGyqI0qrv1PUyxaAvV6m2i+5ux6tcL7/Ew5IcD1tdasmHKtb0QkSFqI5+Oboor+lax2sGhyoGU897PtQGnUF1JO4w8pCNupe9jFhUkGD1MRr1JBCl4YC3Rt3myotHxFOjGPzVCOLUw9hoBTourCVfokausrCtA9FmH0AJLbM4VNXvygBqyl2zONTWb30E33PGoRae0lAor8NFYzsyeU0r+TvjGPz4BjRGMhq52Itx9iV2hTYP/UpPhZobLrQ0Kx6WzFCbrOqHysO5ENPUt/Q1/fUwXNtdpRGv41N0qDLfFhe1P7a4T3YnS/fZ4lBpLJChxV42k0JvhJaSFO9kOc3C7SQyj7rglaww6y4U7bipc9nuRoLJit3Uv3hE/yLcInMtHj3GfhrRzUrjZF9mcaiN4xhWmuDSe2Yp+pv9KpfOlFeeMw7Vuc2BdpcNN5RlPlUhq0l3qgJttYs2BGj8N0TdbO81oOvdKAJCM3h4sdOSuOk5jEvDk8OSaRzq8sfDkU9oYEm3NJXX9MXKvKalwdf7aY4OVdmYNIhFq2fGAl2zJHiV42zI9LXvEtQ9utH1fofBjXI3zN4cxSitBsfvpBHeWyFOqhxFjb8dtOLrPsvMMr9JwnU4iujB4mmuIbOoYRDqBMbX16r+yodk6VDLodGc788Zh+rYE4SPEYXGr9Pd5IsJ+N+LwKX8Oin1oRjSxtixDRHhbXXBe7wXA15a5rtoqyDssByE6UqjaTROIrFtetmAOtSxL0YwyLymwqEul9d0rXAxh0O1dKgNIA30PfrrGPJehvw61Tlvaat7ZuiT1IvY1TgyJwLwlSKarHWFlJ7bGULPm076R97A8HckbiQ0Oi1z3Tv9tO6rwwS/1F49nyZyqGadwMziUOt5LQ2r+5xxqBC/6/f7qdfsR2yMOTa/ZSCBA0wIQQlT4XsnQu/2ILS9QdDlTqOlmRibxDuVIWElDc1rTkQ+GED/W7WFHlzXSHhYIgVfVxNreXg5HaqR13QY3ZLXlC4yjS6WDrXREK2tvfUTVCpDbNv8zMxCYlbWmm0Psz682g1npiiWrW08q9eiNfEo/VDHvskyjA9ZfTcxs0DfNoYbC59c/fF11eD8LB3quiBY88Ot3/o4tOeMQ5WXYdsbRv9vvAjRJiGdpPEQA4h4vF6002WsvVGHYPaj3aFR0s0c/IyN7SJh8xx3IJukVwDVNi3gT5U4n7OVKbe0VNOhSl7TvrO96Ih0YOW8pmsdqqVDXSvk1vtcGQlcY1M2F0LvnVlqNWvzIPJX5SEC19h+5WOP0khOOdB5cQDOL+mT9uZR2HI3EHtUxfes8tn1/jaRQ7V0qOt9eTU8/7xxqCWQiD+nWL6vZilbqr+GT51hO7HHx2hffqTSKRyle0sOgxglUdWOlAVPWUPbNT2yQXSo+UeGe0wwQEnbOz01Db3+SpYOtX6YNeaJP2pMM61rReemB/qL2mnWb9uSZ7jBGbiddqQYrk5CDza1mMihqhieTZ1c9cbNMOSoPpIWXH0OOdQWQFV1YaMlsf5Eo3hZh70tiZEvxqgSytDKmP7jrRiEiTrUks2FNqWh+/1uOLh/ic+prYm64+dRh9qKZbRaH+vnUFfrocH3bdvbGXIsi8JTG7y+Gcb17MUoY/lie6dKC9Xg7hY3ZyKHaulQF7+Kpvx6XjnUpgBzcaMOXwTd03lGRqIlK4PX3/jVELK2IE5/WEvKxcVtremXiTrUkmeAJAnXqSIbuDzUEF/TleBg6VBXgk7z7m06goqtPnS/y4DazF7hskXRlWekl6fUn77asTi257Iwoz8rLZAHr8SQozGT51AXet8iUjM5ceY6r38Vp0qWKaCYM7WXPnKOcgiZyKFafqjLvtDG3bA41MbBsrKlNoYEPMRUbeTOcLgb/e4QcZhucLvq8NV5FKc/6xhSDyk+dgVpUNWN0C56FCi8JT7PEp8PRonPVcKQimTLBB2qgEECN5z/1XlMiq8pg1l4mBayucXSoTYXvsu3Xk4ulq+1ke48ySD2VQKuI1EGwxY97UBZKrfaBqo729H1tp+Whozo9Pko+r9yY4iB/G1uLzrfDcE9S8Ony2MYbnPiDJMfl5f5ANvlF5v9XYm3W29QIaIqszhjR8Mi9dT3chriJlJfl89Fbe2bUfR9nEfkHO0tdpLw7V2MV7UAQWdgCN9PuxFuY8rGm+MYuzACNwP429xFfGYM8djnI8RnJ4ZeqWhfOFQTdjsbY4/3XxpkJp8sE3IMw9cwX9MVIKbwVqyaW11EDdf6fUpUBmb0Ww26JiyxasOo45pNR+7bNBKzcbTvJGcp709mQXFsbQhDUfFLpQCDPhTuMMtGJgdtiw+eF0tRWzzwk9DGHxUY3aUsLBrfXG6KLgU0sFAnbTnxin/ofP/N+S05STXJqiNBTFvQX2k+Ip4y+iUUFHybM79Sf8rwStyg2JfAmWkPWjxfE6LLcH09D8WxnRHUiLOSmsx5zFeM3SvBHShp2ipIvHqxUVwc2mnUcxdSdJ3L0G7ChsiLTKeoLgs+MyrTA+IzSn0U2yWHWnhKPGLgf1WavZ7ZiWzyceY1jd+8oXSmPp+vJf3r3C905n1t9X4heUl15Vvc2v1CuU7yfda2iorroUkfm5CguhglKYfh3/QxOtMoIyfR2IF0xrOPcT7fo6inHkDRBSeTZoSY8hRt8vwUs+bQR86zZ7H1oRC2LN0KElsScOcodmbHwtEIAWjmpxA1cLGqpNst6K98PjOq30RT51fen8BRsp2k0xkeVDIt7TeXp1vHvvZ6VpBVt1YIcAnbHDpSXw4g8aWBNxpxLPx2P/rfqzfwCznU73iw3e6Db3vZAKYZT/xbMIjEYryVGjZyqMl7SWUA1Qq8FcOjGHOaxniA6DhJddROL+J3GEWOpXK9N/q3BOUQItPy/YL7lBBVyaHczP1wEbwIT+lzPkWegrB5fzYfQRXiQtFsiBklHIzqIsgB6k4kMXJ9JxQdaUYqic/60XfIW/YGmFT70wlkiKz9FVkrnC4n/AEGkDhIwt2QmJtl3a7wNc/Evak0E/ceYaLvFhaBrYRFixxvbb+x6zGVyF0lGG/hfOMMlVmYnqnvUNbC8W3mrnTqUIOdTF5xglwppZEzBepBKYNweup3d9PvMX8rk4j73+ktSw+pI/npKBIIEm/L8dmAmngHhA+HWyNyZZfia5phUgCP14MeBshovt50YXVk6ZqTeTDJ+VZLAbJQr9HfdErQYvRnbvl+QQ8PjZyxg3Y1ZpfNR1C3Us/53gA6CTld5W1cGxCz1xjy67qGjnN9ZVGcaJj0xQAGkzams2Js4MqmFdGuj2w35AWLmLfO40Jj+pVeTZivDN6MlWlZ+TZk2VRrxObyMoavB/nv6CrDzGsS4MHGdW2oTqo9scw1Gib1X7gBHDyN6KESgtLQ8OogA0cQny9UwVtpSnSoCo+WabeBl1Ve0w/7GMPc2/JDsJqGrGMz8qGS/xfOtNVF7Y4m6G6rzdOE6VcbRn3XtG8mMPDxKJMKM37w2R74ZtOIUwQbPVFLCDMi3/URnL+SQejnJMwvlZCSxPQqDRquaWyThk77qxASQsssa9tWbQaVb8I0P1QeXlpeLCvf5oGcCTRiHw1jhLG9tYIXPZ92w5ZkdKa2IHoqDP+WHcSTJM6fHYHmi2KAYmIDc4nPPByf/4qpIom3nS+W8LmiFRKZVhxKJQWbuMdIfOI+EtXMI+ZpFSlai4spfqgk4yKONaM8W9lmWglB5kMdGWPsYEZ3cT/SgO/ZuZ5F/KscQjR2WDXjDBF77MoIbqQpJv6KC/4KjY58dJ05YcPEp5Iazg37571IfEy5PM37+4js86RVOFQ5CZmwaMyyYjONQ23lmir1ZXGoJUg0/FO/x2Ti1G+GTnQid53Zohxu6sqzSCWdyBPHXDX0mL46hNFbabj1MfS/NgZtewDRSDtxf5T47MTMl31If058pj1FH+0p5vFW2hYOtckhJEp5TbWnOYx+NWH4mt4nMW1mbrxl4GYGhyqHfjM4VAGBWftjJfg3HYeqMylyatqFo+92wfGbCVrnUhOzzQ3n9CQzZAhkK6dY8XuLG53nRhFi1BL8YQYzXO+SFk6ilkQv8bpY0s7wOheHfXeFfqfEoZoANbM4Y7M4VL6F1heLQ20azHMkMjpFvn5fO1K38vT1piWqvGTi62ooWxqU93gfRgMadDKbM3yeClh4XG5ELxBvaWdQwmc73WiWlBZwqBL9KENf0yFy4iUbi2qxfJeMreEXLD/UhoO0xgZNIA01jmyZaratbjpTpDF5Nw0nXSts9Eu98SCBws5gbbkVqbj27OH/Ku276BvnqnJ9/pKJHKoVy3f+LTTvi8WhNg22ngMh+K5S5HspjQLd1NIXGO1sihzrOwyeUmOvNlrK+nZWq0zXm13Vrpddk8NSEznUYRLROK16By4NwLt/wQfWyDbT6uOhOTpUkdyZwaGqc5mlQy1b7PV8Zfq2rkNp9H88gCwPpcgk4NwRQvRsuMzir54G66hrIof63OlQ63gtDatqcagNA+WShraH0HfOjonrNxCnj6Skjut6M4LwSyseYZc0s+YLcliqmReur5exK0xLx4ASwqGGKixrDQ61vvYaUdsUHSqJmqVDbcTba2kbNvhOnsHowU6k6RM6Yxd/UQZlaGCqqWWnYyKHapaOoFmb0LIwNvOGxaE2Ffq2XQFETjLZOMW2tq0U17YqdZvMqkk6VOFKhz4eYl7TKCInluY1XS4falMBzcYtHWqzIVy9/U0n8i1No1x8I+YGLSkmcqiWDnVtbzgrVpZ0/HZvd9PychXhosWhrg3ItTw1m0eSxoBDV8aReUzspVGS73AnTr/dhcD2WrWotXS0TJ0m6FBVXtMPe3H0px2IvtVdtWNLh1oVLA29KKvHsvJdM0gZkOEr+px9egPpbJ7GRC7YdvgZJamPfmlNFh+ZyKFaOtS1LRiNxioDlweY7s8O104XPDRAEyf79t3tygqz0g/SDB3Q2ma2uZ7SvxlH/+dxOA5E0feWG3o+gdExikp/2A7fz+uNlLSGucthqYE6VPE17SUx9fvo9iN5TZdhTSwd6hreVZ2PWDrUOgFWXl2/T/P7qwno+7sw9K/8sIvLzDUGyv71KKPr9KzuNlPeWL3fTeRQLR1qvS/LqO97yYeOxx30CexF7ppE59EpaqTL1Q7+p4Wog8HLPYzW493jRX4qD8+OJh/K1jaNTf9ULpsF6M7Se47RkhjhDExp4dH7MPQtrfMRWNkYsBGzb6AOVfKa9r5PX1MJfH+hX3kILDdES4e6HGQae93iUNcIT8VBMCxgx5tM3bRHGgmQiDLG7if8uswpcY1dLX3MRA7V0qEufR21XhHdlsRhHrw4qJzsNSY3kP8p+m2ouK7cGIXguunWIZysVRoPAU+AYf+SSeTuM2y9BF+gP3iW+OQ5SOv8xne3tEX1XoWXWV8R9YEQUykDFwdWzWtq6VDXB+9anzZrf6wcX7NJUGV/6//t8iHYFsPoB68jd4Qm97OTSF5PI8fria/GGLjeheChELyrYak4wYmpdT0QMJFDtXSoNS4dbtJCJLNMl5V7TPeMe4ypmskgx99GobWnzU4/SDoz0uHeS/Fv7/uGdWbm24y6vtrSqXEkVrUKCNjzcfS9E8eIWwhqDrmnxEFnGl3X+c72dqH/g86l4T4r2lgUVKUe3G2EDpVrSzjSycwkhj8drik+r6VDrXyBjf9t6VDXA1MGQc4xwkqWvmyjuUk4iVQFBmOwMULDyOUYj7xh2PcFSVAFzNVLhv5ww0wkniU+ewJd6H4nMo/I2tdjNO+Pw/PGGfQwa8WiYiKHaulQF70J9UO4hXniyQCxQkQTyQTyj6lbf4GbNNeGd5cXXq8kUwhhnKqBxJ0EGLYD7q1ORtYK0zqzm1bixnue4abrqmeTXjok68qyEKA1PuP3dkwR6RhQBS/41WHWRpwqMJCKnaL25THWaFTUPYMfTyBxPwcHE4x3vEvL2heN44/GgPn9DPDgPDmAM5V4K483QIc6+OtBlcFl8GI/fGW+pstOmTcsHepK0GnMPa4oK1LSmkG51YeeS79DN3Vh4tIhhgbC7isOjpCVTVRSJy1faLLvDaH7QgfDn5Eo88TZf8WN0XcC0O/HMXx5CONJO6In5TVVFLat+jFj021RYO+KGSv4Vl5r+m++z0WJ3LnpSh5LlT7vcZbJmvMQ613hQDOZFImnGJwYxDMYCMJzUnSkbngZCEB2aWkrySwYknqPbxDtJLLdFNstcXOQTZd9WaUJEGAu0863FgIerKUHW5uH6d7OoHurHSmGIRy7yATjvzmDwDTx9hIDKySZfu+IOKdXKevUoYqv6fjEOK2STyPAw1mtxdKh1gqp9dWzdKjrgZ9skkzZpoJOC5GjiE/J0ClJWomUGl3SCGUvK6rigt/jRIyJhxX53NqOKDfaAhMhLxItFWvLhxDrVluCCkFYRGDKxtPMr6pfEYu3uGg0DkozEpYU4TqzTEVVoCFI9gnTlEi8UL4DZ5sTQabRi9L/T1xiSqHelhtqgum0JPnx6Xd7EX0jCpfLVbVqq99t1UE8qxc1HoQe5pBX+Eq8nbHBtdsLT61uM9sZKakIG/8+D4NEMOqSIC4JbeRsPxz6AHLLHXZFh7rcvVXgHb9JMfXHIzj95ml0viJ5rmovdrvsF63FIbEDcMp8W1wEd1o9VzVFs/qtAt81LrEqLbXqEjfF9PVRWvrGkVNUkH9IXJ2ig7kYqc/AQUviRrKA4CmvQYi3uhi+0MvFGCdRVY0vmtUMc2WmmX7KxvCF7h1iMbpQpHY52jTyt3BneRKUDPsulUa2L21Wa48USHGG0m+1+/XMVzazErLZSQxVLFY2qk2T8+SBJp9nKDrOM0vRbea+pPgiN8n7QtSdDooLGVdZotAoC123m5aVDgVv4Sjlvcgz6g2o9yYjkxEbReCXeZBBlzjfH49gRmP9qQVYSi2prTGUJSwrXwNoDf6rM+3a8MVhjN/he+U71WcZk1fnO32tBwN/VRHIftW+NYruSUwZbtQvAV220ErbYQfzXShDp6qPk0MVXXrpYCrve6X1K21I3cyDLPoZAcnJNef1+eZxcLXnS/dzXMcz3zuYr1MkaguldL90pZG/c09lv6BYvNX7BVVO9ZbhAAAgAElEQVQwGg9NjdgvaoYH8V9UPxulbD6CKoh5ZRRZRxChfU61SAtUyUgi3/IFuzqAmVn+0giyWzvQf7BCV8qHea5c0oRwwjPU98gGbXeSKHDzLj8HColtxu/C95wgS076Vd+MP83qr9SFzFUgoRFBQZ3kav0Zy1rgxs1DNk15Wm2efDZHzoSprXLkMlPplHJRKUiSaSKEEEzbD23Ua7rJrdBXlIZCIo4VztPtdEsjakhKEiGt8z3oEgzd6KH4ScLKb+XwMX7bIPDrZJYTJ9+ZJsjHzVxKZX1p17LyVaBp+B8tHUcs72Qg+z74d8iqkvdIiQ+5zqWYtnL3+dujGL3LOMAMN7pI5821tGxb5NhEZaD07sXD8krrWdZtglKSQaqEggEfouRORcJRrhJY6XmZgdyX9S1rzk7craV++fpda31dQjuy31bvF8Y+xf2Cc5Wy1vGrh+t5Xt7nBqFkG2QYJRDW9mljPN/o2/3o3FNb/aW1dCQ/7cPwPQe6LjAGsPKLK9YqIpvoZiuLbPh+n18ZuDi2OipvN+23+L0l7qYQejnQtD6qNkyknLgeo86o/n5LxDNxN0GRLfWeJKaFPJMZkLO0t9nhY8Lpki+oGA0psS0lBIIY8dtJtYnJptbS8gduAsxiQjlFS7t9HjpzMJCGj8ZffhIn3zrChGrfMHXbrxNwH6fo/v9n731g27rOfMFfWqVDvid3yPfsKTkjt2bH6piqnZhqnDHVJAOzcGdNwzMIBbeIhHTW4Tg7iZxgY6nBG0cNBl45i01ld+tICZqWCZBAMpBAMhBD9EON0LvjQAzgQAyeDdF49obG2lgSLwJ4FxFA7kY73N93LilRsmT9MXkpWeckFsl7zz1/vnu+8/0937ezHAfJHnHtzIe3Cr6UUAM0EXh3epcEbsE5CXTv2+XjZ/+ix2MWajT+SVyZF4RJtKqIj4F4Ilu9XwizEqWvgt/ifUoYc8VsW71fzPNC1x5B3RZEyDuG6JsnkHucMXxJDIXTdbppX9m9FCmVkZbe7UHfuTyCx3oQmranFqFDe0dOcbp3bubKIYn3lIrhHjaFed7DXS+VJLO7VqrCTdXvYiuE8BA7Z4ZRq0Y/J/Gk40+a6qa8pMEjCCV4govMh3+XH0561koQBVHb3o0hEQ5bYGw1QTW9fDUxrcJSgm17AM0M5NDzTNTUSHBdZfMOtBwI0wFwaVKqePn2vDYC7Amj51DJmloaLWU7rsUFZVRKqCJhLqXI2pXk4OItPsBcq3dbq0tqTzYoC0tOjoTN0tVY03nN9inZry22Uy8E0cW2y4Weq9112r6SiTgGJEnxJRcBSZ40b4OHIc16d4fnTcs2a7BGUnFRsSQJ4+kORF/npu9jOLRfBUy5hC/HTk4nN4+EqjjgGqkXFDGfNZHq/yipa1VPhIsQOXW+k+pbsVnKERSxgSqOhivJQ69a2XzE01bC/LmZp1ZFI1qBNG/tFlSEpWy6alOuPmzXWw/GJ0MYuca4ynQgcjD3sKxnU7251DedR/LCMGJXmLZxKoLwJQbpYAab8IsdCG4V5lck1DuZ4Gk4U0JdkNhOV+IXvv8eHosR7/G+NyKLOruVPzrfd30OdT6oVPaavHXt5btSmDL/6eikB0fe/gM6dglKmshpq3ctLa+iw4eOU8MIE49NTk6aoBRVGo/Ny2M5PfQcnAc5iWyKE6rFpnu3zaI09gp9CuEUblOI5hjPdaZu0kmIkqdy6niQ8P46D+8Or1J/i7QpUmcp+Pzc2LgrHdI80F9pU0t/To5WrD0Wc+nzq2XNr2h/3BpEz7FOqvtXMhAG4Xi6F7GDXJt0QhPyKGdL3dMewrS7n+5HiA6D8xZhluZjkudUjrzF4zdUW/Yc71myenhOE7N+6nOos8BRlR/CkmkJdaWgbaAdRhyQuPE5ijY31dQyiJx67i792zYusJ2zTyUp1mLTLdp27zLsFd0SW5E4a4iNM8V4q9PnO29QhGcR+4TYOFsYIi70ZBBueju6+Q6EcFqtkl3RBJfzkJZQlwOtZdV1+PxoPh+nViMGm4/rR61nJhmjX4JrIXyb00PJs3vO5emfcn/BIszSwi5L6jE5a9q/QF7TBdtd5IY+h7oIgCp0W0uoKwVkvQOOdAwnXxxBdFeTsqFmJ6luZODtI/9Mr7+VtruU52oooVaCAxPiqQgmVbZpOggJATWvkXjy6JEQSZE4vT4mf36qHTang5Jpkjks78zzuBRwrbk6WkKt3isjjuaMGEZeG0KEvQhDbBhOBmpgYJWXrMk2Q3Z4wfmpvKbMShRua1dHqxasuMwbOpbvMgG2wuqV2B9X2PWsx2oha80awLJ/EDGdXj8CzFEhQRZENSmHZ8TuuYBcuewuFnyghhKqkowXHNicGyT8kjlFjqioOLZF4qlc6XneU9z4xdbpocOQj16XQjxdPH95hyci9x8hurUoC299VRyNllCrBty8w4NWEs/9IicKHn2VpdqWKltm/ak63sqs7mJDTX6eRNfLXWg90IqOl5iKrYJF21ArCMwFmpL1oyXUBYCz6OWNXoReoHeuAJESl20FDi+L9rFQhVUqoYqbvAR/H2MqLPFMFMehkn1Y7KHiXeuielyCI3Ts6jB/S6SgRdgpc5EuBIzqXrdkk507BS2hzoVIxX7bNnp4XMaNFCNWMXYHmhikw0Fm2EYHJUvKAjZUyWt65OgR5UjX+fLCeU1XOkZtQ10p5Jb+nDDfWkJdOrzuqJn5dBh9pyNITHjQfpxODrkED42TWDzlqy63WyMJVdkqi8SvFMdWgiOI9Ciq2zw9bc06ZlQhb6N5rnPu+c47ALmEC0tx5FhCM2ujipZQq/eemK5tmMHlBy4lYXxFxz8PI13FY4xuxATdT889AlOFYcxjQ5Xk80JMHbS9qrym8zki3uNQtA31HgG4xMe1hLpEQN1RbSKByGAUBoNte+hIg69Yg0nGx85QvfkkD41Xk+G1UkIVdauc7+QcJYOK2HgiTBllSGYdcvVuB8PvcQOQw+riYas8bSkBOFx3ccy4A5iLX7BAkb74IKyqoSXUqkFassEMJG0IMhZu6iyPvHGtZpk1aizpRIYElfqS6hYyS9wopvsQzU0Xc+BKtpte2k6FqFajaBtqNaB6Z5taQr0TJku6kr85hvG8C/ufbYdjchgGJTcnzzva8+PqOGRVRdRqSKhEaLEDT3vX8oiKBIYXFa6ciRR7kzrfSUK5f89+dS5OiKeE61ObQFFyXRLwVlCpVhLqzNa3gkGv9BEtoa4Ucos+l5cEFFT7SojQ/HlGzTLSlFT5mBW+DzK6chsq8UokUong1fvrXuWIt+gEVlhB21BXCLhlPCYylJZQlwEwVVWCLt9mHkseDPcggfE4D3hLKLsbCYykRpHdymACS2UyScAk3iQ/KNExOES5VEv1aYZSoLo+l1gpAsfK/FxJUec7yRmbHrYMUMEUZHK+M1U8oiIH073bGPGJZzyD+xgSkQ4b4nWb5rEWUe8GmVDd6lIrCbX8lVg2Zy2hVhzUBvEzOeGg5/h+tJztQ+QUg4EkqXV5jQzwpB3BF2hLXWqvPGojUYzEqc4m3v7lx21KeEtfgVn4XGpbJNQiPve/0a/S+b1CourbXV11s7ahll5A9T6F+dYS6jLhm0mMIPJWCq1v9+DIwSS6GcUk/iUPeL+ThLuREVNeDZHQLqVItpoIA+wzo4x4HDJjxRE6I/gb6MZ/1cyrOJah1PtIK155sQ2e8hCDREjhhEqIebfe1PlOhuBLlYLCC/GUTCoknopYEOsl+bVw7JIBRfJ3iupWbKHzne/k03frrmr3aiWhVm1Cd2tYS6h3g86K7qXOD2Hougddp8N45bQLwx8OIibEbYsfobZWBLYtmZwif4MBF04PkBE1uIMyN+pznQjvpcQreYyZXm30Bh3wdjJp/Mth+OY2W2SCh88OI/JeBF2MsCRJ56tdtA212hA229cS6jLhrJJI8yjI+LUMcygyQfgLboxdpVq0jvbD7T40z0WgBdtn6rVd7ejd1wmHLYPhV5k+6kwcQy+4MDQ4jPSObgy86cDAsycQOeedHTNUJNS5BI/XRNqVIyolJ6FUiunOSHcTVxNqFHK8x8NgCBJoW7KolOLZLoUwSwPmYllwQlW9USsJtaqTWqhxLaEuBJkVXxeTRZpSauxCHB7SUbc3gHZvsTmmNksxMplny9L0ETamVgwfjygmN3XmpGKqm31HkHqbeLs5jMjxJsReZ9KLM034w3OzEzoI3kY/YvhD+iJ0PBtG26Hwiue0nAe1DXU50Fp5XS2hLhd2dYyue4sBHQ4FESH+zYj5lKEm6aTDWL597y0hli/7lTizZqHaaIN8yyFDpE9N5OEJMVA3ka/lcSDKHJqpSTMAv9SSlyZRhcRJSIhc+iaJ6C3J28nvEtCdhNVJZyGxbTbvamby63YeUWEkGKYku5ci46mFpGj2ey8jX+GzEmZxrrp9hU0t5zG7XcfyXQ68llSXrzJzeQidEhRfNDx8SPAoP8VzqJNu7H+uF33Hl5gP1SXmHrPYeVzOyT0hfWMMowbxf18T8c4FH6MwRc6OI3nYD2/ZGsozi1Dk3Sg6KJmGn+tY0tArVUnwyMpit5FzMYMzWtntvJo1KwagzjVzP14NzH/ZkrNi6vfSBxcJD4cHxLZIImgCsfhJLHVvbWaAh2WW2/SevWxH4FgTbJMxnmulJFm0yzgpUeYTWRhFVZG0nKYjhXjbSrJqZUcl9CRfp6hqm3c0q5B8EizBwQhDQhDE2Sidof2T0quglBBFeemm2phXZBGozYUTECKywO80w/+Jd6+kglpK/eW2v1D9XE6YFbPfu41voecXms9i9Q1qIsYuJ0H6Zul8RcMQ4HvXpYIQ4NJ2+VvRdpiaGSayMNcR21f4QYe7xmaFG8vqcYo2WB6/yW4PUTNlYJhtNW8yVVROsaFy/YiGCOVpGalmFn8E3yMtiH9qao5Wuj4XW7/l99PprArfmeGZeSv6k/0hLQ5gtClbvl8wWEdpn7Jqv5B+RENoNdOy0HrlUlwbRSKr2DZRZUp7Z6AcUVY6/Cmei3t9EMktQXQ94gI+nRsYneG364ikZQRVFqsQz/10DvJ4TY5YCLsE6c6rlEkkmiSK8ox8KuInRFSIJT8pDxeJqiA/ry/1t+I4JTLUCp9Xbh/L6G+6vo2WWz7Hfpc13unnVzZeQRIhppbPl/1KCjddKgcBcSByMvdt4ABxpiLN0iP+HBOMX7UhfJoZoiYHkZP3VmxbaXL4+46sQcTJMFW9biG8gp/Lwb97WM8M8qn2ERFSl4zv99Cfmhf7MhhRzmr8wZSINBlr9wvZb/m+y/fpiiyzFTayZgiqo7EFgYO0l5YRuBXOmcDPICaHzBkYoutUSC1fUDULR5xSqNlq9ja5HkcTvYpnepHE2HLus2VPi3lkZeZWVb+Jg9MYN/qlJkeu2GAI6/SXafiWmJS5Uv2mb0mfDNJRhYP2dxtjNitijS6VhIB3byuCOxlwRPC2ArtN5sIATvw+iRZGSws2sM0JF5zGGPJfyrsjYaW0kqeUeofHP/sW73nvdm8lp7doWwZFZckHfEdYz0WfXHmFzM0M7HUpy/cL0WZJMg2r9wtx/Fwt5RurZSCLjcPGQA6hQ1QbibB0T8VA7I0enLjABOPPh+GtJ08nuNjgRdNmBz2AowymwMhLF/PMauOj49LsziT/pywcK4uojuWf1UX1KxxgDYpsRLUod0g2tRjEfdSnY6cfwb3EowoQU+PTCDqPD8O2rw3tfmo/ZI2Q6Q2QsCY/jdK0kkTs0ji8e1tA9nh2IUNaiyWlzCbCTFhYcuwvWwNNi2jllIbOwrlKVxKcoxb9zjfNNUNQ5xv8iq7RDprgge5sNoXoKTootIVx5DgjL9ENP/R0K3xfMlfqL3qQ9oXQdoAOSuWd8MUp9a3FCKKGIGqNGpRaGfprMltuQkqFXwM46y4Xh0AqkaBPQxbJ8/3o5JGb1qMnGXLUhdDRdvi+iuHIs91IbmKA+yfn4K00LWYZ/md10edQqw9xeaumWa36fS3WQwX4xsW6WGX36XrfeXoEHWLjFM5GhkdipTZwno3rOOVTycfnVTcSWooTqgXUaiQp1mITqtmKkU23FsxSzSa8tjr2He7D0CHxBRA85B/BW4W4xNnX+tCudlZemw8/hVmazR5bMnl9DtUSMKt9uRbvd+7s5lt6c+vcf7856xJHc4ckJEhaZjedNXkica0k1NJ4Z43Hgh+rYZFaME2zCy2hWgbqFXW0UryVzsgs1aLoc6jWQL1W++Pc2a0/le9cCCzzt0io80qvy2xnudVrZSOolYRqvXKOb0RLqMtdlmumfo7nxGtxtEIkVOWFaimkRL1d8nu2sGMyPLXQ8Jgai5rsGHcAVxPUO0Cy8AUhpBLYIfL7CJKf8yyblepBbUNd+MVU6o6WUCsFyVXXjpwT73+bMXx5lttKp0JtQ63+UlCa/hrtj3NnpwnqXIjc5bdEQAoeCCp9/ZEXOjD4bsQ671ttQ73Lm6nQLS2hVgiQq6+ZMPFV8gNLlpme492QoyVWFFNCtaKn2X3URkKd5/zv7GFV7VetNHhzJ7Q+bahzobDE3ypq0KW4OmvV9jN6FvpbLFMj1cpGoG2oS1wcutqqhYAcrxm7PIY0zytKQPwW4q2DZ0OtKNqGagWUZ3xirOlt4V40QV0YNjN3qFOInGF2m4tx+P0+dDzfYelBbRlIrTgwbUOdWQb629qDgIQKHTwzyBCHHrT+rFWlR7TSlmp6+d7h+lhlQK5PG+pqYP61yncJS1sRFRJVSYrslgDdWysTRG0JXc9UqZGNoFaL1OotSAFa21Bn1tt98s1ONb74PYi/g49ZqawkpgJCbUOt/kLSNtTqw7iiPQgShp8L0/bSy2gsKWRuW2N/mTUJbUOdBY6q/FiKDdVKR7SqTHJ9Nerf48fAewMYS4whIY6EFhdtQ7UG4Itq8CzCWy2hLuN9u5lJxi0xfynJWF20DdUCiC9BQhVmKnYxBomvvKySN5Ckh2nyNvUdmSTizA+azAhvrUu1ISDe+c56Z03MJtqGWu23a7a/2P4o/i+i/l+JMJRhXuvE58xgxLCzSZr94vy+UNE21IUgM891Uf0qToiSjNVlUQ6sSgNS6u4qtX23ZmtCapYioVIXPfjuICL5fpVKUJIlLGoCoHYh+fkQTv5zBONO5sllSMvEpQS8z/bC66qJcvtuoL9P79UyUpLV71jbUO9YxHwFsUvMp/3rEzypEULLrhb4dvvuqDb3gnEtjpH3enHyAhB6Jgh7MoHsZqYQ3RmEa25l/tYEdR6gLHiJagNR/84b2mzBh+79hnBfVtt+ZNTmXK3xhpwFJc7XYcaUm3XZih9OlSpv4Z5cLhfCTKrQfrAdUXK8AX8AzY944af3qBDXhTDKuTWAtlACJ07TZPBcN/reDCNfI7v4wrO7j+8IE1yD3c5pt36/sHOezhow/bJP1QRvOV+H7e77lOxlR549gnZqibqPdausQ0JUg3uJv3fx+nbYXAjQmS12oRfxlBNDp/pgo9f4QixSDZbY2kVaWTDpiTRG6YLv8ZiOSSI5KnWD2Dh5v9K/BVqSzix5LQm3213x9hceL3MqcuEkryXg2Sy5O6ozv7n9SxLmFOc6ypVp6Xw5w9S1capy0/BOetX5Ynmv5vjMCDDqN+Egn+LtHY8nuBZiGI3HMMQsRc3eZhJWP/bv3Q/Xlhn+VamHyYxxb2UWkCxyE+OIX22Cf/dMHXnPulQPAjnmK05eSc4wplXC1/L1LJv42JUxOB1UNxdT3ZTfr9Z+kUqlkLqZgoO5X6vd33T7fHXGlwYSVI+6Zb+wAL4l+CVvpBi9Lga3s7Q/luErxyECEHcvhbdybErBh8/Inhq9EFVp/Zp9JK77gmZ6vxJVFDMN7HAy6pSKAMW9YewG98MG34K5fUuPVm8l30ctZxm+LJUicUtysdIuI0AWTkXUouINq15apX/LYiAyCj6m0wMKmlXtr3z8XIzSb2QwUr35lffH7wJPSZGXIhNR0gRYMl8SSSF8Pp8PKWYjkg1h5n2W3rOJlBwi1bxexC8nSCQlqXIORiaNoWsDSGVS9AR3I8jE9aWSOt+H3vN55vNtQeuuJEY+JPF9tbl0W39aAIFmX7NS+Y1fHzeJTLXwlXMprVeZlsJdfopTlGX7RTG95MCtGu0XdAIz98US3lRxfyRsZb/wbCTTwly4ZvL4Ur9ln8Rv0VDIvq32FWqi5L88PcCj56NIJCiwEG89WzzMgy2jZ7kZQ4SZyLArgNa2FvQNRhFPtqBpq3l7vr8PFFjmu7Hur8mGyqz3wgVNB8snAc1MZEziwvtKhcRrUsfkyPi9Cr9LkpF6J1Vo/67jV51Wd35z+y9JhlbBt9S/9KvU3JQshPOe6b/0Xs1Pg4gbOhhCilyuSJ0SA9i/y4f2p5lfl9F4BDFnxXs2MnRAypm2Vn43Jqka2+JQm44Cr/5TUQjkDeJucfMsNSxOKbLxVgM/S+tnZr0U8UU65zi4quasp+riU+33C85b7VOlzyrPl/gqeDsD/1K/cz45pu7XujHA0LF8AGLe8RBfQ2JTfbzFJKaldvio7OmZG0xezqOSLpvBPNlkDJi83rFQ8hQ+ogmqAG5uyTNXKsMKRs4nYGsgd0KbWWj73XX0c5vQv+9fCJz89UlE3o5AQlGKejcQDMC3k2ccyf3qUkMITNEDm5tl5NwoN0FqA54l3mq1eg1fyOrqOkZJ9MiLXUpCbaG/gzDFYkedlkgrMFzyT7rMhUDq3CAGrjjRdZqqzot96HmTevZTbfDUbL+kXZGckn0jOSUr6Do5M7FjZr6klLbBRWJBNYgVK0Xc0tmv8RXfiLPY79yXU+Pf4nafup5Ex9EOtB5ohavBVeMR6e5LEDAuDaH/kg1dbwrekrC+OQDP9k747iJRlJ6t1mfmGs0Hgrcbq9XD7HaNm0melTfA3Dpo2uazqF9KclfZr+wXVNl4pF8r9qnZU7/rLxU29rOEIqLhX4RNbVEV9rQqNHnXea2BmwbPCKYYqqwNPjqW2EQVcIY69tskqFtrMHyqCGPvdqPrnRRajv0BfU9ZEKXp5iiGB4eRvEkHmjzVInvD6D7srzpRNa7FMPz2EMZF1T7Ffg90oOfpxV3brXwrolrqFU8/LY1aCfYl9MV4vZ+MwrYrXMRbagziwxi9lofvkRpwwmQO42d60Hk8gZZXe9F72IJ1TAl97NwAhi+nlO9Djtq1rqOER8MSwHcvVajRi9HPIib7BdWqdnq0d75M88cqIqqiBg8fCledAdaBHeYupKk00rRxgZ55Cg25cbptdEbKGHNrWvLbyIwhnmDotE20E1jF/ria0X6sD38YHED/y34YH0YwfKP603VsC6Lz9AAG2O/JQx4k3qcTQG3AvuBkJai6JqYLgqeGN2jjSuXhLsNb8X0Q57ZaFOP2GD18SdjquV64mVN2q36pc6H5YBf66BT0h8EuNGXiiHwYr36/Ng+CR3vVfjFwmkQrQ2eei5nq97ucHriZW6FNsmqLXs7Ua15XfNLs4mgkpU68OGnDrhGkhMh0HHPC8R5zsFqClZwsN4GSItOmzu/RicYKtZl44Clo8w/nmudvR43gXhqG/lxbEBDipUrxHCYxuSYTcGwJEG/pRZofIoMuO4o1xVHStU6xR/mfuFz9QjwtqbTlRAKlVOc61eDo7WruaiMB9dTnMc4zR4CXPtlpZPNONJVcqefWt+C3o4EcLs/RKS82C/qb6SKD6EcxZHfSeF+isDM3q/IteYYOP+dHkZxwIvTLHnitIORVmYlu1FoI2OiMacMI8VXhLY+4CVPmdFtFyubMVrplEBB1/pS7LIdiGVGVkaTogJPKuxDcY4GJiP3lecTk5OuDGLvNBCL+DoQft4KQy0xXV9Eq3zveh4uH8x3I3GK8VRr3kzxrmNzig39rjRBTxifYKJw2OT8rS5Kq3oGrLnpLBiyTFD27gnT2CaKF8E7dTJtTt3LSuq81CgEHmnY3I39Z8JbHlOJ0qmOAjkAtvfPp3FfaNUqfVgA3fy1KVe8YHHtbEbJo37JtbELgyRCCOymEfJmiVG7FTFdfH5qgzvNOPE+GEfSk0Pt8O7ov5tD+fCs8tZTlFYdrrYSaPNePk2eYkPmFI5YhpbwKGwMm+A+G0fGkB0lxBpuY5wXpSxoC80DAtacdYV8afTwu030+i+Cz7TX18JUhKl647HOeYVf0kpIUTw0g4+PedcgCR6jS6OspiOwNIvxiK9z5UQxcypTurKvPWpKJ1QtoGtlDL/Qi8JShbBDTgR1qNWKRTImZpfBl1R6G8WkE3ceHYdsXRsCdUwEMnA0exsusbs8phi0z8rSjUuWe/IyRkhq8cGmVb3WBfj+1Tqec4Es9aCHeih+AJXb/xeBXxNsqo445CiOByKsnMDTpR8+zHqR5ZCdvxZEdZk9K3CYzzEnmr48hNemEz70+Vb6aoC6EEITMtIF/oTpWXWfgZ4+3CY4G00Gq2t1m0wacm23IXhtBz7EB5F0+BrfoRtv2am4LdGa4EkP/Gdps6xxwbmlB16vtNTz7W20o6/arBYFVg7eMAuvZQUa0LK5zteas2pVoUHnuFUhh4PVuMuBOND/Vgc6neISomh3nGXaTZ3+TE+Qe6unx+3QH2ndXtcdqzuae2taRku4JfPphDQENAQ0BDQENARMC2oaqV4KGgIaAhoCGgIZABSCgCWoFgKib0BDQENAQ0BDQENAEVa8BDQENAQ0BDQENgQpAQBPUCgBRN6EhoCGgIaAhoCGgCapeAxoCGgIaAhoCGgIVgIAmqBUAom5CQ0BDQENAQ0BDQBNUvQY0BDQENAQ0BDQEKgABTVArAETLm2CuRYNxhiWrQzVK/jbjoX7CWKiGgdSnccSvZqrRzcJtTmaQuBBHSocdXBhG+s4ahAADLzANpGGUAqhs8nwAACAASURBVBJWeAp5xh7/JI4k9wbjRhIx4rBRpT1i/pEz0fjnccQ+t3i/mH8wNbmqIyXVBOyLd5q/EcPABYbiY25WB2P+5YkseQacdj8SgHeSEYXeTyP0Wg+C2yockYTJgodf60JkKojeY82IHutAbGcPhk4FYVkwMeakjb7RjbHtnYgcZ796lS6+YHSN1QGBfAbxD4cwmmFgfIY/lEyoEjI0X+dl5hcbcSuC7L5u9D7NIPIVLXmkzvXiyKkMOn7/CtJnu3Hkj270nulDsKGiHd2lMWbpusCwpecd6H6PexOzZK23oiXU1frGiYSZWymkElGcfLkb/YNMacZkyVmG93J4A2g71Aqvq/IL1rg0jIHLNoSeYWBx5la01TMXK4N0WkZM5X04fAg/F4BxcQBDV6vEza/W967HtbYhMJVDminM0qkkht/sRhcD1ceYaFzCeRp1EpaPiTd2uSs/RyOJwffjcATDCG13w24j3m6wMS9p5btauEUH45+3ocWWwMCZxHRigIXr3393vvkvLPfftNb+jOr+rBFP/CSIwA/tuDKSRH3oPzE+5/+AR3dsxgO344iOTsDj24EH/88YIm9Fcfv/ncBo5Hd453+fgNtTj5sX3sFvfxvF9SknHvK6VSrV/O0EPug/id++/6+4NeXm9U1zUqxmMPzb3+KPDz6BI4cDcH9jAhfJbaf+HRF04hIiv2N7/8bn/qr4HLnx2Pu/xck3PkDsvxrY9L1GuL9NcXIyiUjPbxGf8uDRv2T8YcmV+NogMs5H4f32FUT+l2Fc+28TuPKvf8SVB76Lxm9cxwdvnMTvfv8RRidsaPqhBy73g7j+0Ueqjb9/3DNnnGv//eoZ3KcQ+JYT3scD+OlPdmDqRhyX7U/g5Ole/MOBHdhcZyD+ny/C+E4zdmxMY/itQeLNBCb+y0f4bYTXN2xG/X+7iHd6+zH8X/Jo/KEXTuGZReo9+zvi8yD+eCOPzY1ebPp3s+GXucDsUCOTCBzpQAsl0uujUcRuAJvqDVx693cYHmd73mJ7JHWpTz7Am72/w3vUgk396Q/gaagnjuWROPNb9P9nA56/boTzGwaivzmJD248qHA+yTG8M3obk/91FH/8zMAPvE4kz7Lf376Dj+K34PzLR7H5u05MffGv+ODSl2j+2wA2zxnn7FHff7+0hLrK36lNUjiw2OqYD7VYsskYht6LIUF7DMiZDpzux8C5FOwMaJ++2IvwMycxZrjhriNhe4PIeY1S3kQC/a/1IpZ2w+8nIrzfgx5ykbPKRArjt7MMTO9hknXzjoNIlmYWmDS5a4+NXPfr7IvIxI4x/GonTl7IwuP3wn0rhp6XexC7yVtU2caZ4DhWtL3mmY1i9FwMoyk+N5VFLBpB7+sRxChxp6+PMkNGNwbiTAu9pwXNDW4zkLfDgyZuDAbzW6amzLHovxoCawYCNhNfBW9tJZMFGc3Ye9S6JJgEfcrAmBDBd5kInPof90QMvS/9o8InBwXY5Htyz8TP+O970Xc+TQbaB3cqip5XI0weXg4JEsirKeQYFt+3xdwv7Nw3jOQYkjdzcHsdSH/QjxOUYKUIEex+bQRZtw+BzTkMHScec/+QlFbpRAxRElmz+TSSl0YwEi/euzyMyJv9iJzluKYyiL7Vg+63RsGBIeDzqGwzVC/Bs4U4nE5hjMR/vRVNUFf5G88zSbGUPFVJ04XZZ+wkeLa6IvK4SDz9QbQ9dwRBco0Gs7U0P9mGTuZxdX9FtTHVTZk4CdwVEq0DISbwDlGdS+nyPNXI5Wt+MktHJKqUnSUFr2SvsMG9JYDgwRA6mB/WNZVE8kqazgdDKueh90lmszjcwXsBOG/FMXhOkJGbCNVNJWYAVD9JCrwibwD7Bn5nIvGeY93o8BPZb5Cwkox6/Oxnr3c6TZyNtuOckaYdeXrm+ouGwNqAQBFfleNgiSEkvtrqBS/MKdiJx66tzOT0VBjhg8wIQ1x0P9KK8AsdCNDEmkqlkMnEMXIhCTQG0PpkKwJ+FwzicnSWKYSE8BaZVbZvL7ady2cBVxNaDrSj7XAX9rO98cvjdPRLIPZhFJmNAXT9cxhtLx3B/gYDQ+8OIynOUhuY6YljNB0e2RgZA/Vbhsz2HUxt2f4qmfanA3AwkXjyVh7OrS1o2RfknmLOy0kzESYyML4Uxnt9FU1QV/n7JvqpEQqnO037SGRNYipXBEnJFTZ6VD07ialLJEyhieSMHURaELmyE1mkbxKZ3iIRe7YL0ZsklILo041KU4IwRAZpX1rjfRsRyuZymQnW2Z6ThFIeyt7KID1FIugx7UE2F3OXbmAflDqFACqJusSZ8wm2otqTZtkKmv0tzHXKsZNYHznehaAriZ5D7ej6NTl2NSazvtiCpjl882H9V0NgDUCgJKHOGWqZpik3ZYfHxfRuxBMb17mdqc+8grhCeCX5MK/niLeZSUqK0X4yrWE6GZFh9RBHvypHXOL5nGTFdmKcYxP3haKfhYN7hJ3t5Y0sUsksXJLfWA2NuM06thSZ2okZpr1E9GWfEeIqWA/iu3uzH77trG9zIcCUjj2/8GDsrQ6Enz+BqGjCWHJkJuzsD5bab1XXNf9TtuXVfCx6APNAgP6B6qpIqGpRyy+1yA1+kSvF+3RikpIrSrS5IlesJFxih3OjE24m7G451I3OPR4iFh2cSNhm5QFmMmL3RmA0TeTi8x5BwBKnzbZVb0Vi63S7+HQWo4kkOh7xwbjGxMJpItw+OkOQUCKXYx8cE+unkuMYpzOVh+OW36ql4jhlzK7dbeh5LIT4r8Nop/ratzeA8CNpJjYnl00VcEn9LHV10RBYGxAQ4iTEaIZIybjLfwuTOVcDpX4L7gqakCDZibeueuLAThLTF4NwUlUsqG7baJJDaVPUrO5G+jlczKijZlT6cB+Q69TwlO8DconSo6fRhtFrCTKuPDGAJMausc3N1HKxL6YkR5YMuNIKTUji8DRyrtIuI+OXgZnFxjzJbb/qQ2hfBK1Pn0T/+SBPHXh5NIjMtoO25M18cJ0VTVBX+QsXIpY1MsjnTAlVfpNSURVKgiWLm/+yE0Jci4XYZvC+8uIhMgtHmp60w7WnDe2X04idjaDncyecJG6O3SGEG8oQs86NIO2hA4MJJDMkqCSuwgkbTFys+mVfuSw3CEqgLqqmOn9Guyzd5LtSbOM27Sy7qK560k/u2kCAjkQ9H/WiG1QFp3kejistKzuBfGbT3BhK4xXHpgHag8k5Jwx4qTpqFnd7nqMb+9IJ32F/kZMuTVB/agisDQjkKVnmJn1FlpdjFnxVScDN8WfJ1ApK8H/YBI+Jq0IE5UpeaZWIdy4/2p9uwcnzPCr3epJOSsRbD4/gPDX7GJs4Qrne7sfo5RTatlJrRNw3sqV9QTqRfULa8yH4XBjJN+goyNMDHjpKjU15qWZuh9dBde9jdEaMDqDv2EmMe7LIidqWY1Oj4vn3LHFfxisleXEQ0YvjHDdxv7GF3svUktF/YpQ2YrevXTlHmTXXz1/t5bva3/W/0azh9OAH/h3wiaqHxf6gDXXu7+PRv/bRi+8BbPgOVUV0WPBQd/QAVT2eHY+i+a/oGED10gMbNmHXjx6F5883YYe/GZv+LY2JNFHC3YiWv242vXKnYVCHTcRF8a5NTG3GT3c1wU5jrYfP7xBv3W+w/X/PdnY1o/HPN8Lz4xb8oD6Pif9rEht8P0XHi/+AHX8mjdnQ+HAT3H+SJ+3djMDf/T1afJvh3cExbrRhg/278Dz8ELx/LjqhKeRpb7nyf3yJTT4SZNp9fa4pRP/Xf8FH/98T+E/kyt2Kmk8PUn/REFj9EPi3B/Bg3Sa4/2oHnqDDTr2ILsQf/MkmPOSnt/uf2VFH7/nvP+zDLsGtB+pg+4sf4KEf0cHv2w8Sj234wcPEO3rUu3/4BHZ8h2bJ22Ssv1kP749/goe+K165ZeXbTjwgZ9f/t0k8se8JbPr3DxDFfWh+2APnt1iTxj33D7kv/JCSqKcZLQ878RUlyS/tjfj5Px3Bz/3CPVOA3fwDNG92YuL/nkLjT/4ef/ujJnrdE2//chPNQXZs+ssmPPrwZkVgH/x6EqkvruP/+dNm/N0z/4D23W5kPn4H/R+mEXjxCH7auP50vg8UWMpei/6qIaC8AKO3PQgdCtZG3UpV0+D7UeR2UoKmeloXDQENgcUhkOfxtMg7SXh+1o7g9jLN0+KPVqiGgQSP2cUybrS/EISrQq2upWY0QV1Lb8vCseYZdlCcnWazwRYNgComMb8qW6xFXepuNATuCwhQLUs/feVVX4v5qH2DquP1WjRBXa9vXs9bQ0BDQENAQ6CiENDHZioKTt2YhoCGgIaAhsB6hYAmqOv1zet5awhoCGgIaAhUFAKaoFYUnLoxDQENAQ0BDYH1CgFNUNfrm9fz1hDQENAQ0BCoKAQ0Qa0oOHVjGgIaAhoCGgLrFQKaoK7XN6/nrSGgIaAhoCFQUQhoglpRcOrGNAQ0BDQENATWKwQ0QV2vb17PW0NAQ0BDQEOgohDQBLWi4NSNaQhoCGgIaAisVwhogrpe37yet4aAhoCGgIZARSGgCWpFwakb0xDQENAQ0BBYrxDQBHW9vnk9bw0BDQENAQ2BikJAE9SKglM3piGgIaAhoCGwXiGgCep6ffN63hoCGgIaAhoCFYWAJqgVBaduTENAQ0BDQENgvUJAE9T1+ub1vDUENAQ0BDQEKgoBTVArCk7dmIaAhoCGgIbAeoWAJqjr9c3reWsIaAhoCGgIVBQCmqBWFJy6MQ0BDQENAQ2B9QoBTVDX65vX89YQ0BDQENAQqCgENEGtKDh1YxoCGgIaAhoC6xUCmqCu1zev560hoCGgIaAhUFEIaIJaUXDqxjQENAQ0BDQE1isENEFdr29ez1tDQENAQ0BDoKIQ0AS1ouDUjWkIaAhoCGgIrFcIaIK6Xt+8nreGgIaAhoCGQEUhUFfR1nRjlYHApIHk1TGkv8wDTjeatvvgcrBpI4PE5XGgsRm+LXLBLMaNBEZvAc0+s17+dhKJZAo5Ps7/YXN70bzNA0d96Ql+5g1kriUxlsrC5nDDs8MLT72BRJz9GvKQDTaujnyeLUzx9yY3Wh7xwWHjdyOFeCIFPOiB7zEP5FKpqL6vp5Hb0ITAI67SZfaVwLhhQ9NOL1yzHjCQupFCKpVmn064G73wcm4G6ydvZZGV/lnkw+Nthne7a1Z/0x3oLxoCNYdAXuHUONd/vs5JnPLB00A8IhamPk0gM+WCdzfxsLTrFvHZRnyWNY+JFGKCV1N5td6dbg8824kv5Xg7RXy5RnxhH5jG2zzxdtTEW7ZtI+6W2sizTssu7guqDRnHKFJTHNs2jm1jGcC4HyQF92FH0y7/dJ95jil5LQPbVh+85YjLcWSIt+PXU8jbuH94iLdbHVD1OYc056D2Dfms96Llca+5d5R1eV9+LeiyqiCQuz5a6HsuVAg84i/4H/EVAgfaCq98lFZjzF7qK4RcrkLo+EghNz3qXGHkeLBg2xYs9MTNq2Nvhgt+l6Pg2upTbXi3+wtt/zxQGDObKRS+HCsM/CrMPuS+v+DbHSr0vDdeyKZGCq8c5O+dvL7VU3BtdBSIeAX/dl8heKin8PEts9PxdzoKXoet4NjaVhhKTQ9Effnivc6CfyMKju0dhZHrpVGmC0O/5Bh3hwsjZfWziZFC7wtthcBumatffYZ+NVT4IpstjLK+h/17d/LebhmDvxB+baSQnd2d/qUhsDogkEsXRk51FkKPFfFnZ6DQcXyooFDu67FCzx5fwbOlszD61cxws3/sLQQFn1//WF1MD3cWPPwteCu46eOaD73wh8JoqohH2XHibUchWMRb/85g4ZX3xgrZW6OFzoNBhbe+bZ6Cw+Ey8VbaeLJnBg+J3+GttgJs3kLHm+MzA5Fv6Y8L4S2ugmOjr9Dx9sy97B97CgGOp/ODL6brZ5MfF/peCBeCnKvgrf+xQCF0aKDwxddsJtZb8Ndx39hCnFV4zc89PYXR0t4z3cr9+aXEK92XzMLam5SB6Ns9OHkhj9CxHoR3uZGfJLe7sSiNytuqtysOVOQ2U9DLq982cqAiUUqx1fFOvQetL/eiw+9E8oMedP2mF5HNPvQ950Xi3X70/H4MLUd70LHPA0ySI6Z06Gjw4MhxD9rZRvJsN3oGU2h+thev7OU4hON28UY+idilFDlWcqSTKUQvJhA65JNuVZFxOR2smIlh4GwCgV/6OU6Oh2NzbCiTqq8No/vlHgzdcuPI0W4E/OTc82mk8m44WT3JdhwNLWh9tQdtXnK+5HRtG93FOZt96b8aAqsFAplLEZx8Owrbng70Px+AjVom1DmK65ULmlKjw+E0pbbSoO3EDOKz02ZXmiQI3nKNtzzTi569xNtzveh+/QQijU3wveBH+hzx9t1RtDzbje6DlPgmDIgEauP+0PEacZ2apOSFkzhyahz+X3Sh+0kveyLebmG7LMl4DOPwwr/NhrF4FMlDxGHzlpJoZXy2iTTGzg0jfvAV+Imuap+R68W9JX8jip7D3Ri+7UTo5W60Em9drJWkhszJOnmOwW6j5urJLvQ871eqJRv3Dme5NKxGc3/+KYLp/pzcmpsVVanJ22mkPa0IPxUoLnZBimLhYlXEkj9LeFD+rVRNPommcG8VFakD3rpWDP2mB+lbVBPBg6Solepa0HYoCN+che7aRhUTa9m2ulknTdVQM//NEEJcHUXsSh6BZ7rgvBBB7DxVSE9RfVQckBpfnQfBvR6kLoxg9JAfAfYh10m2i4hpYPTNCKLXnejiZ+c+6VEKEVx9cjMSNTM3JB/VVZ4GdVH/0RBYtRBIXx1HFg60/yIM//YZ7CwN2FYnRDM3TZjU9a8Fe23ICV7LBWEaiSfOLU3KtOG1tSI2HEcynVW4k0wkYXN5EXg6BP8W1cL0Hw8ZXCnOFBnkuhRxvwXebSW84o0pqpPJ4Dr97WjflULvO2OIfW5QBV3EbcFPmwOePT64MYah8yn4nxL1NEc2lYOd4xfymjgbwcBNG8Kn/oCeg+yrWDw7zS8ZfnCW8HqoIt46c79U737/1E5Jq+kNi02EUqL7ygC6j/UjdjXDJVxWZNGLTYJl5vrMt3I0znFZK0OMIAFtIymXG15fE5+0weMTu2cUJ14+ieFPaQNRLc7+k6fUKu1l89myG3nEzsUoRdImsjegiGb6ehTRqzMt5GlbAVGy5clW7HclEfkwoZ5XxJQtqppE7tHLabh2hNiGq6z98q9m/4Yx03b5Xf1dQ2A1QcC9rYkSmoGBV7sQOU976eTs0eVJlGxkc0WCmy4PCh7nSaxK+FzEb9aVK8nLY0hOuuDbQcLGpz0+L22UcUSOncDgJ8Tb8raKjZbwNT8Lb9na5zFEyUe79wURfLwFngn6XVwcg2CrKtxX8lNkw3fuR/seNzVUg0gK6j3IPySm5n5C6fVSEu5d+9Eqmq15C+fD63naZNdj0QR1Vb11F9qe76LE5kaK6p0j5ETDRyOI3ywSlSIHK0OeIZ4z38pJjx0ZDB1vx/6f7kfH20k0v/gKjjzpUrP1H+pAFyXHLNVU3Yfb0fqLE4hdK3+a7Qvxln4UZ6oeo9NEwnSa8PsQ2EpE3+OHh2ra2PCoqiu11HPCcW9uQXCfF5lzQ0hk8nA8aI5TqY6oVhKVbr6BDMQCOhIbuWWDm0ffcyTMP/0JfvL4EfSf446gi4bAKoSAa18HXnk2CPetGE6+GEZ72xFELs6sVxOPFpFQiQsO4vjo6/+I1iC1VKfi8PyiGx1KdUv9zZOd6Hk6gFw8gt7nBG+7yczOJVyUeAkfZWaZhhOZ6gsxOhy5SEypKt7uR3CPDfFLMSQzpUrETyH6GzwI7AvAY4xh4HxGSa0lCTU/mUH6OomyzQV3uaNUqQn5FDW3LYOxwW619+wP/AStv4nCmIf4lz92v3zXBHW1vcktfhLAIQy8KzZUJxIfnkTP61GSxxKxIpmb5mhl8CZHKJ/lRald9oTQfqiNdg4S6PODGPm0iD0bfWh7lSrXD/uUDTV9kRLx8X4kynBT2Syl9TJEyCRGkUhkaEt1Ik0Pv0ye9hly5Slyv6MTZu+l+iJf+vbuh78uQfXR+DQnrO7TnmQTSXsiSySfr5icuo2I6/ELYQ4iEKQKaTNtULpoCKxKCDgQeKEXA+ci6Hk2AFwfwon/mRqgqxys0iwJmRPZrayIhEo8mJFQTSz2+AVvqZql2SQdH6afQlGLRL+I0Kt9iJ77A8IHPMiSsHYRb+PTRFHaLkqI5fvBZBIjF8jC1tHeSrNS5jZxjxqr3GVKqZdLRN/cP4yvcnBsC9BD34bk+RGMpckM08abE2Ir6t/6PLLUQmVnbzczkxK8niJ+e6iaPkC8pSYrsI5UvwvIBzPw0d9qAAFyed7HQvzHYyp/14r+BNWsk7SbiAODA0ilyygfh5fmb2ediwufC75Y7FS7Nu1pR9tePnCgGfhZO/rfHODRl07TNkvkcO0MoGNnC2sGEKb6Z+xmHr6dZhszEmqpRdo9L9FeKqosOkuEz8t1Ig//T6cSiF82yNmSO1UrSrCN7Wz0o/VJH3rej8Bo4Jh5T9138EiNx4HElSjtOO0IF/uUFs0iSMlv4lj1/CsIbSle1h8aAqscAo6tfoToiOd10c/geeIURcDQdjuPoVDdS21OVvCnKN1lv6TDoSESXVGeFGJEzYx7TytCok0i7uRpk+15YxAt/lfgIyoLcXZsJ96+RrVtHXHnjTGM3zRAr34FGbosFiFU+uQpNzojJb40YORj6Dk0at4nUeSIMPp5UhHn0t4hamnKyQi17Uf01SEMnrMpZr5JNFX1Th5/8VClTT+Kz8Lcn8w+ix1Of2SnHGimc1bnC97pa+vliyaoq+pN85wYF7jBBeluIFeYjCF2y1DcnkPwYwvPitL7Z+jcACJc2O0+N7KJAapmUnDsCKBly8xkcnSRyPIMWea2A9kroxiV86bitseS57nVpGFjH07kblK6/DwPJ8+7esrOmc1IqMJZs9xkG5+Qy308hG46M7nqiPxEboNef/3Hoxg9H4OxL0RCyOuC1DmDn1QLk0P1nqH66zxPuD3uN826vL7/cCuGX+6nHbcL9l/SkcNL715ywam8nc4MfF5WJttKp1Iw6IGsxlPvoKfkzEbBGrpoCKwKCKjz1xmueGpv7Hl6v18Yg91Ff4jNsl5JYPwu2EjY+t8chufZFnrWj2PwDPGGZzhDtJGaxdTM5DJc82wrmxwlQU7B3lhc8xl62N8GmgRvM8THzyhd0vnIXYa3OeFwVSl9Gqbj4KQX4eMdyglRSZriof/7fgx8FMXY05Qk5ZQAn8tPiQMUv5NoB7ePoPutKPL1ZMhFkUymvflnITSfO4n+l7pgY3sBwdu6HNIcr+cRcx5CqLNfcu+ZoGMjcVjYBfFELnkKq+Hdp380QV3iizWuxREjPWnZ60P2Mu0RG5op7RFJlvj80qrxcPWFAZz8YJQxDuzI0rsPjUG0v9BKT122UO9D+LlupH/dh6HXuhAVZpIqmpw3hI7nyDEWOV8JxpCnamf4tQ4k3XZKsGkSZXKzT+1X0mmCffTS4y8jUuBXJLw2LzqPdqDFVTZK3ssYQhSlE7rcX4xiOG5D6J0OtFHdNF1I2NPneQTm4hCiN4mYHGeWNlJBI1V49GX/gRYM0iM4rdozL7v2dqDnGNB/Joa+VzswsEHUuUTl3R3ofZHHDvg9TSIeOfaPiG7gnRxVyKEOdL8U5Paki4bAEiFAPIjRSci5Kyj+7RglDjcTh8to0BIbWqQaGdM+Mc2IBPoVJdEpEsqjYbQ+Yq5W39NdCKd6MUztTvtFaprIPGapGwof78T+nWadnDCjGfoknO5E+KwdKQY2sbn3o/NwSEmnqbPcG95KKOZS8D5Lb/quY8TbLWW7EPE2TVNKPl+8doPH1y7QMdBPExIJZzmKOzNxRJ+PEjcTaDlAvCV+SjAYs9De+ncBDJ3l/asM1CJ7BYtrdxi9p4m3JLQREtRBwVvivGtjCD3vhNVukaOKOf5hD9o/43EbmZMtiJ63O+Er79xs7r77+4Acr73vZlXpCRn0Vj3Wjf6LebQSAbzxQcScXCS/ClV8c89Qehy7nEQqk4WTEqnXNzsqkkwtTw52VDkUkGyJG7147ZXtEMZVIgo9e5Wdg4ggdZofZzsNJuLmb3JjuTxKhwQ+v9GD5l0t8G2dTaaMq/QKpFHV83iQLvo2RlihLSdJO9EBSpwbZwM483kUA5ep4qLNxDuZQPRSFh5Kpj5GiVGFnHWUiJkicQ2KI1OR8Ms9mUvyCufM6C+i4vX4WhDY6UKG/cWuzImU9Ag9FPeIh7IuGgJLgADVmonz/eg+OoT8AZ6L3JPm+es8N36qT+es4SW0dtcqZoQgrmMSH9RT28PjXi0756xViUb0mfghpMjEuim1Eu/KIn/lb8YxfGGcRC2vnHgcgpvE7VJUNCUFJxhx7AYZbZ4IaH6cODYXb2/EMXSJx938tF1u4/nt28THi0nYfCJxzqFogpfULOW9rQhuy1HLlIDBs+ohRj8zi4H4+ShVyoxwRkcl/5aZPULN9wojrRFv87TNSlSoIKNASX+xczxVIMyxEGEhqPXE+6dm4/1dgbmGb2qCupSXJ6EAKZUOv9WPMQdVq408uCwL9rE5C3Qpbek6GgIaAtZAgATVoMQXfbMHkQt2hJ71wnAE0Umv2fWgfrQGyLqXcghoL99yaCz0nbY77x6qM+lynvxwCCmqWprK4tQu9Ji+riGgIVBDCNTR5t7gRdvPAjyOQvPBBWo+aaLQxLSG7+Q+71rbUJf8gnmwmu7fLXtAb9Yq2GCWPA5dUUNAQ2BZENjahOZGmkWotgyUmUaW1YaurCGwBAhole9iQBI7zIc8s2l44KdN0KB0GmLAAl00BDQEVjcEDNrhIxfT8NKWaUza4JeABWX2+9U9ej26tQgB6lj2FgAAIABJREFULaEu9tZ4NETCeKXodOPZFkLbnpURU3G+SdzIUN1ElxpCXdROyhuXLjailvLSHCvp1HiOWm6oOjxSzc3ATHuknHduG3yQDgBbeOa0fGOgj33yJj1r6dnnpiOTS0y709dkguxjCx1+prlzOj0wMENKvG55CFuOpIhrv0vqkGnI3+Q9Bt42eJ1P0qmJYQvLHBKkxenCozmJG3kewWGQbOWExKM/V5P0EJY58GmesTNTwNHzmIEavNupcqPLfuo2445S4i9PTSUOWXSnUGmgxPEoczWhHKsMwsMmR2Z4DGFmDpwinavSExIyTcZPsHEuLsY0La+jbug/6xQCPL7BM9KjDi+jjgVmrbUlA0QciYiXQpAFb831LHjDFpgEQtaz4Et6Gl8En3hLcHoLnyGOpXifh994jet3o6zsYuG6zcizxBWbg/foYMSnkeHRuTTbUO0wWL6nwSWx9c0ywRSOxHXpv3S0DcQLHyOXgb4eqRtpnjc18ZpnzJRWbb6TZnm2k2RdhxzFK+4L4vSUZNAHwaZSCjizH3rxMsa3h0EdUtfYt4xV5lYs+dvEZ3bp5v4h+5LgZUrwsoS3ag6OUnUYUj8jY1Q9qXk4tjBwi9o/pqutzS/3ZxKd1TarXGFM0poxDZpvu7fgbXAVXC4Pv/uYnixQCL/JFEzXRwqdjzB9klyXlGq859/dVvhDQlI3ZQtDvwoWiMwFmyNQ6P1oJpVSgYncxphOjcdTCzxYUgi/Pqom/8VgR8HHdEyuLV4zNdo+poF75+PCF5I+6utxM50U0zx5JVUb0zx5tzL92zuStilX+Pi5YMFbz9RpMl65/1io0HFK0qqppmf+fJ0uDDznY7+uQuDwgJmqKjtaeOVpPr/NW5BUUq6NTCW1ld9l3ns7C0PJdGHsdFvB1+Av9F4qa/BLPnfAW7Ad6CmMqTGOFXof8arnZQzyL3AgXOgZHivkmCaq8PUXhYGnfeq+jNMvdbYFCp1vj5altpsZqv6mIbASCOQSA4WOA8QPwQVJacj0al6mNPRxfQcO9zEl4heFocNMNciUZSa+cJ1zHYZ/VUrJ9kohuIUp03jf/9JIIS1rt1ik7badjgKJV8F1oLcwLqh+i/vA1uL+oFKjBQvhl/qmU7iNMjWjiVOCt9wnOA7/L5k6jc/m4n1qb/EQ5xXecm8JMe3iyJUyPFN9M53iP3M/ga3gO/wH9azgvbSt8Ii46pH0jw2ci+DWI8SrD7hHcbxBh7cQfK48jSKfOx4qeLf4C32XOYivxgt9h3xMA+dSe5iPe0tgH/H2HeJlCW8llaPsPSW8Je6GTn18X+AteS5dqg8BZl/gucv+xnaey0riJFMtjWRb0PFqO5o3mRKgjVFUJDi1d28Y3c/zzJxIsORX3RLkgGpnkTKd5ABdPL82JsEfeBZU8Xx8To7Z2CRh8AQPUItEzdp2ftrovh94pgdHdgKj759EL4Nq2xml6JUnTQ7U5tqP7lMd8PKcp0iqwkFLyQsnTlf3/TwqFPTQnf6dE2rMNnL6vYdmJPT8DR4uv8IYo9t40JzfYzfa0MZExGGmZWvlINKXGRrt1Cg8B3jm9Bc8HM6AFR5Kuily15K2albheDlFzqnE+Zrz8GxtxZHf8IxtlkeXft2DvpfZn7cPIfYpD7i3MsrTsS4EeIZccfTkuEstzGpf/9AQWAEEbFuD6DjOoAhcs8kPutF7PsuUhoyvy3CecjxGjpDxaCuPn3EdHuc6JGcrCiYXj6qpIhGGJJ0ZM9DkP2eksQmeBXWZtyT4vcHzqt4GaaC4agV/uQ80+cPoPMYQhpeG0HP6JDppaoq+RucqqcbjNMEXzdCkqiU5psPrSqPE727uNX3PNCN1iedWTzFetwRkOB2eOXt7bYzBXHgKVqRrHlmLMx6wh+dlvfs60e+nZHmLcXx/cxIxWwDdDLoi+4NIsqAEqyRX7g8zOMZvHLODwVdUETym5One0YoOPttcl2RbTB35ehauXQMIb5d63NmIt+0vH0GIQSsEXnK0b6ZNs6m1+FcT1GW8NYNqHVHfkPtT6p9lPMoFQ6RSiETnJqp98nk5R+aHr6i6zV/jqmJxcmG17GbIwfLGRb3DVefYwTOajizD/DGCSoZex2wvz3Nn8WsSNzcAO0MDSj1ZmOqQOBe3m+nX/HsYschJwnvhBMYSYzyTR+RQRM0L3+NUtcxaBSbxltF4d3F8WwGfjVFV3j3BqEVUJ4EqaDU2ZsPgWdgx/m5/sRmjp4cwygPiQlA92wkfeX5KCPQYHHQI8VF1PV24YQjxm4VAREIJmyb9mteL3zbQdk14EHroEAJ+lOok0Ytvk/ssdsJxD+dQrgI37+i/GgLTEBg8M8gzzAwKUgzRN31jsS/i4S/4zmK7QiLKXMUenun0PVJavRmFS3IW0+cnvrhmNygxcCVlYmAvTwjEGekokaEtl5WYV1jF0WVbAZpAYszuZBZ+krkVFXDLI344eJogxZi7PczylDzaYuIGQwDKXjAzhpk+Ba9cxDcxFXkZMCLB6Ey9NzNKJTtDyBmBLctIa8+T6A4OYYTjCklfJJpqpluAGM/r2jbyNxNhlHKm5jlVE2/n4imvC+bKPiJqXI7fPCfr4/7GdHATZLaPk5m4xXvEW4FcngEhvISXYiZmhr/mv+ljM8t4hWNXxtD7Wg8StO2tuHBNKWLGxSecWako2yp/qMVWulj2qa4Lp7mHtiBKa8mkED5KgVfGkSIHHPA3wybtCYfIIhKqFKKm+pT1LjZGp0Q2kaKIaNkAzKv8q3pSz5XuJnmAOyv2S29RKpa6DK8WO8vwao37GXeUZ3O9TO0mwSYkUkyx5GUvKSFZ6SI/S3khS+2rWxyvhE1TtmV1YWYeZj3ajq7zuLjYcjabJF3lkWT7M9FdyjrRXzUEihAwaK8beH8AsXgxju0KISPERJWciXvlzSisKd0vu6HyiPK6mwFLWjYbTOw9LqiopD3xPfAxOINnVpCJIr4SH1Q9EiiDiGR3M7A9r6m7bI9y77zF1FAVMUt8EjKiQRLbbbG64O0FRmJrDKDtIPMhe+yIC7Eun5JsTNK/Io5l3ZA5MI8cmUTRvGOOV+1fMn8+JxgueG+OgnO+Qrsro7E1MX632a65y8g+eL8Vta3eb5Oqynz48hOfJRg6bJjcJhdikWtddl+ySFnM/IgzTysHA0pZifO9lMQGTKLraqVKtk1JX+opSnbuHVyYmxgD9PMxhBn9KBFPwNZA1TF1PglZoMX2VUxP8VBmyL/Bm1T5MjFwwuVDp18OtTPSCks+M4QjIUqQXPr5BkqAR3sQ3GoS4fwUU6e9yMTklEkNOjs1H+1k+jdTJSzPGpJfkXjiOkjpkVK1j+3m3yQnermdZ3ZdUsUsxfGUfgqaKaTkWE1UnKmnJFTWN6/zk19SSaqNQzE6MlE6tjUhzHCKMkaVUorwysSZ1/WZFPplDmhBmGEMQ8VwbzN96m/rGQKK0UtSOrwQZeYihrUsqVeXCRRzXQqXWL5y+Vt20UmmbXu2FRHGuM5TsguKWpjJu00Jlfcpcfp3eZj1JU6TB8dATVHqa5pkeA3kz0uOdQo/yBmnGTJw6P0sjEvDGKJDpP9lSqTUbAkrb2c4xaFXWzFO/a/gZoDhSDupdTKJGp2N3utC60USRGpybIyC1HM0xNjbfJBFIqDF4pSZn20mkaU2jLmRB07x2uUwtVyz8VZmOc1EyMNUX5sSqoyyBAW1M6nxm3jNPuttyDIUaU/bGE1caToaNlG9S7zcxodkPxD4X2dc4+dbMaBignvRSvNS232At1pClYWyhJK5nUGUgaQdVAHFqUbJrzTxteLguKZkcZb1W+LwlLcf1bTNO5vR1EiLYhF31Qc5VRvD9/m3MgNEglLqDWazuEZ7hahlSFxKahdpV0moXLypC0PoG4wiu7WdWStod3mMXKIicuRx66h22c6+tpMgNkqCZHNA8ryNh+LFa0+YyhQD6ztINIvOgLxLdS+53CzTtzUzULeowt0NTcyhSI/Kz2ZStanWivM1W5a/wvnyY+519VuIaZEzl02L43SIfYjewE6ZCwm4h1GqTJBw/EKUeZ+OV4QX1UvbJE9jEWAzHepv6xkCXCMx5gLNGVnELjIGt3jIrrCY+CqyYTnmFmVF4ot4mKt16CHeFNehKaFyXVMl3MRwhM6vGDb0M+LulRRyDPPn3ybGf7Y3jQ9cv8TD/K1RDJweZFpEZlx6tRcnD/uLo6Ymh/fd9CJuErzd2TRrzcs+YnPTU34LE2fwZIFB7VXJi1fGnbocxyj3HvEoFrx1cMx2B006kmxc8LJU2I65D5Qu8HNaQhUsLhXzm/Rbwmv5tIstl3jrJt5mbuWUIDDzDJ9lVh3B2xaGPfVuJw7fJ3hb3EJLwNGfC0FAYt+OXxvnQnFihPEvQySqkqdz2UURMy5tWZxlDwuHKnjl2bMfXa+1wVV2TwiHIpa8JiSneQ8dfGiTGHqHQahzLkqq5E6nhHdli6wr7Uo8UBpuETjaj15JUEzKbKpreFPak/437qdEx7im5QNRaCT9EJHp+NC2kYHFn+lgkOxBtO4rppAi4Ry6JEcJ8hg4FkKUq0hstkY9s8VciiPJIwpMrmGW4nyLv9SHw8HsMXTlSKtgw8U7k4zbSybF3kAHB1mVAg+xJbmZqur1Trg/6WdigH5EPowh8CsJkM+kADLXTTwS8WoP/CWVVnlH+vu6h0Dic2ZWoqlGESmu12Emcujc1nmPcJmFMCY+1TVTCqOGp2F206aESkmSa9XFVIm+DYyJPTgAJ4/QNUkMbjYV5z2TyZVnibeUOt10Sup7M8z7xIHp7uQetUv19Cg41I1X9pDbLSuyhxjEGR9Tp/W84EFsUweOnB5AlKrdDqkrtlrJgsO9IfpaO2JFPDNopsmT2UjSYaqEt4LP0q0ikqU+uPcJmZVjbAavmSjO3Khf8jfbcApRFHwXvCSzEBa8vM1941Av+t6hduBUMfY5n8+7mtBKeN1vqRm1hFpaLHf5zBMRYwwSLUhZIkoJsccIIiy3FDnReSVUaYuELitnuNhnuRRMtJruySHG/A1JZnwYQs5J4rWVt6RdWczF9ks2VAfPgIkKpjRusxETWaQv6aPUl9BgzpD/5L588h9zmopDRZoMRfRSRiogQ1tpgoy+9yCzvzD9WseLXeimp2373ibYWG80YdZTlYvjUd+Lf0Rt7WZi8uiZASR4ttbgmbg4Vekx8gT+Hc1wS9fFUuT/4dgdpHrKgbGP6Ah1mzfJZUuRquosqoKXMXsDUDX0n/UMAZFOx3gu2kliIOs9JsHg5fz1PRWFKLNasFF1Ket4Ni6JpkjWKfFJiFe9F/uZQjFxpp9e/pLakIwui8rkMo0npqQnmhcnVbozxFRVLa579k8GVPUl657ErFSUpCg/KDG3SIIKF7NOUZskI85fjTLBBfF2H08SEF+7iLddVLWGGajGQcehoXgp2bip4ZJnyvcNSaTRsouJx+MDGGLSc4NwzHzKxBgXibguSpoN0i8xUvYhJiVXZTsTWjSSgeb+KannSvuT4G2WEvJceJkPrd2/8pp1WQQCSSLk0LkRVSvLhSzbuKQ1amsjB0mD/7IKF1uWB7AzX0o7M0W8c8FchKNn+9F1mzZDOSpDQ34ruby27Vx8IsFRolNCnYup46h/HSJBtz9OVSubkeATOSGOTMcmJcc+1IKnqqvES6obxT/Zrwykrw2i85mEImD5STeCh19Bx0GqoIikGW4OSsrlXH2P70cLUzWNnI2hjUkB4mdHMM78iv3P0y6ydabVgJvjv9CFCOu172lTttl0JgOPSamnKzoeaUX4ZwlEPqIb/S9i5MJpM2KqOue+DiK3TxFJQcocEZaJsEznLaqugrQZR84MY/B8O1oOuWEnjJKJIfQeTWNAPLLyzDvJNFmdTxXbmO5Rf1mPEMjQuzXGtINS8jSXCOFKpehdy0xMAdpSl12IY2mmJszOYqTZrly/PcYjXVkMMfhBnuvQt/cIel7yq3tZg0zypNheXTyeQm3SRJTZX0ictglZIVNL3E5nuc5lQFzTeeJslinY5iuC58bNcaZmPILU+yS+xFXb4x04WUxrmCbeunlNiuQ0bfb2o4eM63CIppIPmDmGx3R6nu9k0vOy1sWh8EInhn8fRQePuMmRPZX8nDg4S0J1MKPMS2GM/k/Mx/zyPyJG50DjFlXXTj/aX2KKOZqdJJCFmg/nZDoLOrCffhYnLw5j4MMEgs9xf+Gcjc9HmMGLaniBFzHezWxAfYdKau2ysa2xr9/8F5Y1NmbLh3vy1EncGL+Ch35Ee+PDj+LBuilGJLkO9/c249G/fnR54/mWnYKujW39BE/8aDPqiyxN3beIXBs2oemHD8H9HSfcf7aZyYmJdGzf/e062L+1AZv+yoe//ZGHz9iweTM52MZH0d76U2ymjrTuG3Y8wOcffeJv0Pjdetgf5DV3IwI/Fi/CYifTI30AdvtGbN7xA3x/M/vZyO8NO+hm38RnHWzrQWz+YQuP9eygfUaY3U34QSMJGMfT7NmE3L/VoWnvz/H3P6b0W6bjqNv4XY55M5ybOO6HOU77g5ySF0/8+FFyr4JtxfKNenj/5qdoeciL737bTg/GRvztz/9HdP1TCDsaimP9Bg+/fZP1fvw3aPYRTuxn01/QLsP+679LW9Vfsm9bPdyNzfj+X2yCx806Gzfjod0taGRfc2dc6lp/rh8IfHT2I/zu9xG0ULW6gaLe5u/9OY+90bmNm37rk61A2dpdClQe+OaD2PQ9pmUjTnr+Q2mFEe+4Vht/+AN893tcn1yHG7kOmx7ehR1/xWTj3yQefseDH/9NCzbzmfpNrPOnjcw/+nM8scPJdWrnfmJDo+/HeOLhzVzTNtQ96MRDP6F06d00Zx3XYcOfbIDzO9/l+iee/Qe29ecbscn7EALy7DeI1//Ri0eJbzu4B4iPxPe/Q/x2bkDTDg/qqA5ufvzn2P8TE5+m50z8/v6fbobnL4g/f93I/YV4y+Nonh+1mGMqg5PT8yifp0PTdzbiAWyA779rx39/5J/IaG82m6NE/sC36JtBr+a/YZ/135Ljuhzrf+RYXZz3w27uLxvg+d5DaPreJjh5z00tWqPPz72leAJhemBr74uO5bvIO5OwYz1Ui4j6RAzoKXJkboeDjgWSt3SMB6dPMuSea5FW9G0NAQ0BKyGQoWak9/VepbIMP9uBE8e7ETrYzmMkTOBNNfCRF4/A/9jal4ishKnua3EIlNisxWuu0xpORgDpptpVDkoLZ5viWUgv7Xx+ngeNfxInworaRhcNAQ2B1QQBwcvWUOs00RSfBTe1OsEDkoYxQFWmqRZdTWPWY1n7ENAEdZF36NriouXDlEDFzml645rIqDncRYCnb2sI1AgCjo2OaWIqQxCvdtNISU/65fo91GgOutu1B4Ey7fjaG7zlI6YzgpJIZzklWD4K3aGGgIbAciFQ9LZd7mO6vobAciCgCepyoEV5XqmKtFy/HKjpuhoCtYeASKim/3jtx6JHcN9CQBPU5bxaLaEuB1q6robA6oEAJVQ5oKGLhkA1IaAJ6nKgqyXU5UBL19UQWD0QoIRaHhxl9QxMj+R+goAmqMt5m1pCXQ60dF0NgdUDAW1DXT3v4j4eiSaoy3m5RdvpSrNVLKcrXVdDQEOgghAQG6o+4lZBgOqm5oOAdq+ZDyoLXJNwYBIkP8vjMx4Gc1DhAgVJ5UxbNT85HjntajpEWdBf2XxUbNCy31WdZ6mfEvxLvy38lDOKNsZQ1eU+gwAlVAnokJUQfxIKs5r4WrZeFf6UQFl2vVr9W93f3HlYvl+IIp9ULMDAO3PCSpWgbumnJqjLALcE2PZI+D0vg7s3MCblNFKyETlKU6XfaRLyJPM5BhhMwiTe1e1PLUzOJ8f4p7F4HPtlsVZxfqX+SvCLXRqFjwH0nQxJZuV8Rxn5KsVIOl7mrtTlPoMA16+XyembdjSZE7NoPY8yiYZ7E/cNpkIsre+5671Sv0VzlmUc4OGzwyqEYSsjQ1mJPxKvOMH0cIq4WQRfmZ/sFwZjlzsYwa7WRRPU5bwBCi5CSN3MNehyuZbz5L3VJaGWYNUul8ULhoy825G0dq6ElIPZcTwNDOZtsaTouM70VBoj7m2trtan+V4lUpKleEtYuBm7V4JMWBGeVALlD58ZxNBHQ8wi02P5fuFgco4UiZrVMBZGQiTj1VC0DXWZb8HMCrPMh+61Orkw1e+9trPM51VUKFFT1aAYNep3VnaNGsxbd1klCIgNVaQmi0vua2vwR/K+hp8No/d0H/cKmohIZKwuciypFvgjM1XmMKsnPE9/mh+fBygLXiJCKk6oBoip1EULDqx6N2p11MD67YAwlKMVGiOqt5hq2XKNzqEy4ZKpdq3i3KPnouh5tRup22nmrmHhGnZuqEHmFrU/VnGiCzQtLMtqkVD19rHAS5r3MqFVs0hJtZLY1tNheNl0a8EszbvY9MWKQqBG51BzX9OEUaVdNk8Va/+7/Yi8GVG2U3s9ySnnKX4e3KkqCr4lNUa1a63wR/blWjH/5bCp0qsu7+I++l5DCbVWHNhqWKSWrSAtoVoGass7qtE5VFNCrfxsUzdSOPn6CUTPx5g4PQcniakkAHA4mMeUzlfmuYDK93vXFoWo1Yii1Gp/nAuPGk1/7jDWyG9Cq1YSaq1sBGIXqUWpSa9aQq3Fq7amTxKbWhAZU0KtrAFDqXiZ3zV5Nckp2UhMnYqYio1YCJrH7YZVtttZL0/tj7OuWPKjZENdDcy/JqjLeeU1lFC1DXU5L2qFdbWEukLArYHH7iMbqrfRg57jvbBvsCP3VQ4nXjuB7ESaR0eysJO4Ojc6oSRjq19LkaBb3e1qsqFqL9/lvP0aSqjqPNlyxlqhurWSUCs0/OU1oyXU5cFrLdUWZkmFR7F20CKhqnOmFexWVLqBfQGV7zVjZGDbYEPH0U6l7uXpcR7R8VBCFYnc4lJjG6rFs523O01Q5wXLAhdrKKHWykZQi01oAehX/7KWUKsP41r1cJ/ZUAWMYkcdeDeC0IEgwofDCPLTZqeESgJrN/19rYW2tqFCE9TlLLkaSqjahrqcF7XCulpCXSHg1sBjNbShVstcE3m7X0Vfan2KEZFYWn/WCs9Wj4oYJI5Klpca21Atn+88HWqCOg9QFrxUQwm1Wki54FyLN2oloVbWjWOxWRbvawl1iYBag9XuIxuqQD/xaQKxizF0HO6YDrnn2+5T51HNt6NOpFr7orQNVUuoy1pxNZRQtQ11WW9qZZW1hLoyuK2Fp4RZuk9sqOJ430/ptMUfUGreafBzf3IUQ6LmaUu1vGgbaqXN5Za/whV1mPksipHzCaS45poeb0NoH+PGcpUmLw4j+kkKeTHoTzGgdTCEtsfKAqXXUELVNtQVverlPaQl1OXBy+ramSSGGRVo7HoWTk8Lgk8H4a0HkheGGSA9ibSoOeuccPtD6CBOzyr3kQ11+NwwUtdT6Hujb0GHJ7GiWl60DXU9ElSDgebzMGwOeBwGYmdOIF3Xg87HmVnlwyEM3PCg46BXRfxwOeYsyhpKqNqGasH2oCXUqgE5b6SQupZC8noG+ToHHAxUL9lfPBuXrtzPG2kSTSZO8LiRSgyjPw10H2tG8swAhm87ETzoh41Mr9s5B29lVkJsayShOioYuD2TyWCA8w0EA/Du9C7wvhjkoSYSqpzTX2BIVbysz6HeC3DpJp5IjCFJ5ExPEnmYFsnT6IVvO6VMErzFiwPePSF495k1m37Tju5L4ySofN7mRsuBDnrMzeFuyxqtRdBpYXtqIqFKvzXYhATcNZkvN6GlraGyBaG/3h0CJKTDDI83dIEaoS+Zi5QZUWTTlVRbdqcbvj3taKek6WtYnLDatragY1tA9Zf/JIIjx6MYN5phq3fD/2QYnYd9C49FSagL367WHfuDaruvWPMjH44oGHY+13mXNmUdz8NU3OWJSt2qBf6spnOoSyJBlQL2PbVDxIy+H0HkbAxpMpt55r9THKds+jaqeRr9aGe2hcBuerktNqtp3M1gPMVk4T7m3ZRClUX6VhKG4SaSkpTMbYcbQZaHpyVPqAogxPsiOarNXzizKv3OccUoCZV9WNFfaT6S4abUr5kP1Zr+5VWo91vvsnS+MkdBTl0qBIGJBPoZtH34tgeBA2GEmePWzZR8glcGAxGkrycQvRBB19ExdLBeaPs0Ys4/gDJJL5XKkCpLe1T5cp0aqSRSk/ytUnnN8zgl1DwRSdZ0aX1XC1/L28/lsnDkub/IwrqX/YGPS2SkyHsRlVVG9ie1XufZf9R12aMs3i9kjjXbLwQONWL+y1cbX/EaKPkMom+dQH/ChuChbjQTMT0u5q7k0PP5LNK3kxi7GEWEEUNSz72CzgMLS5jls82cG0DsthftL1N1YjNAhhnpaD/a2yLwbG9F+GgIPtcMkmcl0XciqdIjSb5ORdxkDPynxlKlT0PyMfGf2I+q2c8d8+AizUqORYv7TRsGRuNjagOycr5pbvJN3mIC6vKFor+vCAL5KQdaDnYj6PPTvDK3CWqV
D
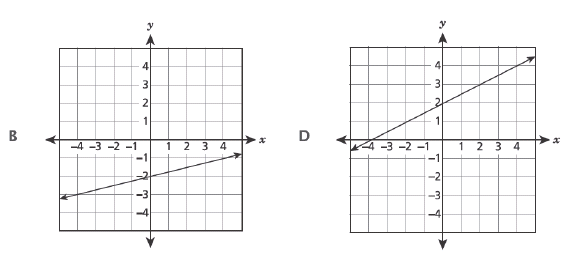
Which graph represents a linear function of x?
B
Which function of x has the least value of the
y-intercept?
A) y = –4x + 15 C ) y = 2x – 3
C ) y = 2x – 3
Which expression is equivalent to (5-2)5 x 54?
1/(56)
Which set of ordered pairs represents a function?
A) {(2, 7), (2, 8), (3, 8)}
B) {(3, 2), (3, 3), (3, 4)}
C) {(4, 1), (5, 1), (4, 4)}
D) {(5, 6), (8, 6), (9, 6)}
D) {(5, 6), (8, 6), (9, 6)}
- Find the equation of a line in slope-intercept form that passes through the points
(-5, 1) and (0, -3)
y = -4/5 x - 3
The set of ordered pairs below represents a relation that is a function.
{(−2,8), (4,6), (10,4)}
Which point, when added to the set, would form a relation that is not a function?
A) (0,6)
B) (4,2)
C) (-6,8)
D) (−8,10)
B) (4,2)
- Determine the number of solutions that exist to the equation
8(j − 4) = 2(4j − 16)
Infinitely many solutions:
8j - 32 = 8j - 32
The table and graph shown below each represent a function of x.
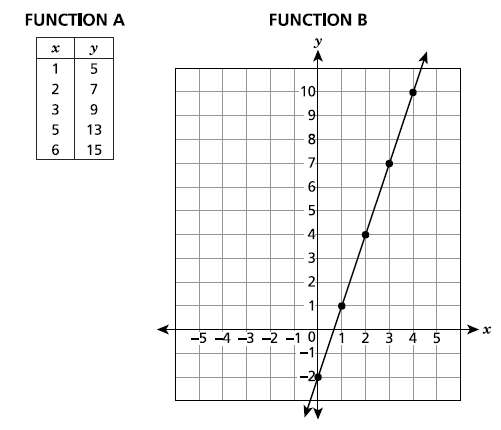
Which function, A or B, has a greater rate of change?
Be sure to include the values for the rates of change in your answer.
Function B has a rate of change of 3, which is greater than function A, which is 2
Function 1 is defined by the equation
y = 3/4 x + 1, and function 2 is represented by the graph below.
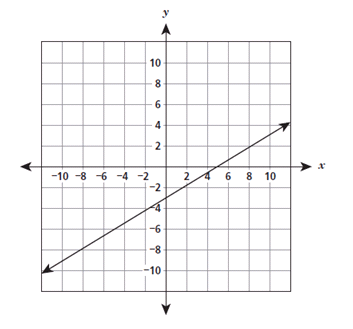 Which statement about the function is true?
Which statement about the function is true?
A) Function 1 has the greater rate of change and the greater y-intercept.
B) Function 2 has the greater rate of change and the greater y-intercept.
C) Function 1 has the greater rate of change, and function 2 has the greater y-intercept.
D) Function 2 has the greater rate of change, and function 1 has the greater y-intercept.
A) Function 1 has the greater rate of change and the greater y-intercept.