Clasifique la siguiente Ecuación Diferencial (decir al menos 3 características)
\frac{\partial^2Y}{\partial t^2}=2\frac{\partial^2Y}{\partial x^2}
Ecuación Diferencial Parcial de orden 2, lineal, con variables independientes x y t, variable dependiente Y.
Resuelva por separación de variables, el siguiente problema de valor inicial.
(4x+xy^2)dx+(y+x^2y)dy=0, y(1)=2
(1+x^2)(4+y^2)=16
Resuelva la ecuación de Bernoulli
x\frac{dy}{dx}+y=xy^3
y^2=\frac{1}{2x+cx^2}
¿Cuál es la solución general de la ecuación diferencial
y''-4y=0?
y=Ae^(2x)+Be^(-2x)
Resuelva la siguiente ecuación sabiendo que y=x es una solución
y=c_2(\frac{x}{2}ln\frac{1+x}{1-x}-1)+c_3x
¿Qué podemos decir sobre la transformada de Laplace de la función
1/t^2
?
La transformada de Laplace de 1/t2 no existe ya que la integral impropia que la define no converge.
Encuentre la transformada inversa de Laplace de la función
F(s)=\frac{1}{s^2+2s}
f(t)=\frac{1}{2}(1-e^{-2t})
Muestre la EDO que modela el siguiente problema:
Se arroja un objeto verticalmente hacia arriba desde el suelo con una velocidad inicial de 1960cm/seg. Despreciando la resistencia del aire
¿cuál es la altura máxima alcanzada?
El máximo de la solución de la EDO
x=1960t-4900t^2
es x=1960 cm al tiempo t=2 seg.
Por la segunda ley de Newton
m\frac{d^2y}{dt^2}=-mg
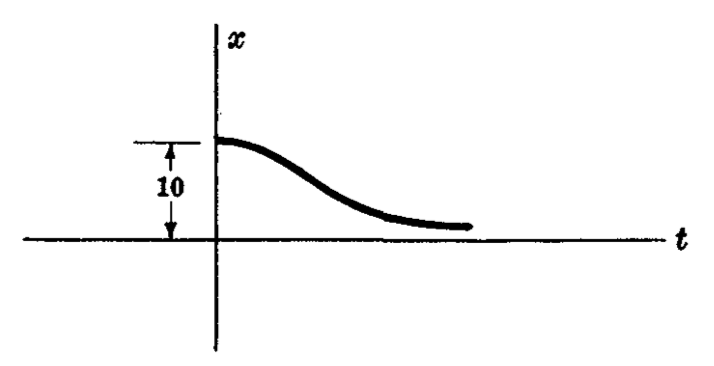
Una partícula P de masa 2 (gm) se mueve en el eje x atraída hacia el origen O con una fuerza numéricamente igual a 8x. Si inicialmente está en reposo en x = 10 (cm), encuentre su posición en cualquier momento posterior asumiendo que una fuerza de amortiguamiento numéricamente igual a 8 veces la velocidad instantánea actúa. Incluya en su respuesta la EDO, la solución y su gráfica.
Ecuación
2\frac{d^2x}{dt^2}=-8x-8\frac{dx}{dt}
Solución
x(t)=e^{-2t}(c_1+c_2t)
Gráfica
v=cx^2
es solución general de la ecuación
x^3(\frac{d^2v}{dx^2})^2=2v\frac{dv}{dx}?
NO, v a pesar de que v satisface la ecuación, el número de constantes arbitrarias (una) no es igual al orden (dos) de la ecuación.
Muestre que la ecuación
(3x^2+y\cosx)dx+(\sin x-4y^3)dy=0
es exacta y encuentre su solución general.
d(x^3 +y\sinx-y^4)=0
, por tanto,
y=x^3+y\sinx-y^4=c.
Resuelva la ecuación homogénea
(2x^3+y^3)dx-3xy^2dy=0
y^3-x^3=cx
Resuelva la siguiente EDO
2y'''-y''-5y'-2=0
y=C_1e^{-x/2}+C_2e^{-x}+C_3e^{2x}
¿Las funciones
x_1(t)=e^{\rho t}\sin\omega t
y
x_2(t)=e^{\rho t}\cos\omega t
son linealmente dependientes? ¿Por qué?
Sí. Su wronskiano es diferente de cero.
Encuentre la transformada de Laplace de la función
f(t)=\sint\cost
F(s)=\frac{1}{s^2+4}
Encuentre la transformada de Laplace, usando teoremas adecuados, de la función
f(t)=t^2e^{-2t}
F(s)=\frac{2!}{(s+2)^3}
Un objeto de 192 lb cae del reposo en el tiempo t=0 en un medio que ofrece resistencia en lb numéricamente igual al doble de su velocidad instantánea en pies/seg. Encuentra la velocidad terminal del objeto a partir de la ecuación diferencial que describe la velocidad del objeto como función del tiempo.
La velocidad terminal es de 96 ft/s. La EDO asociada a este problema es
\frac{dv}{dt}=32-\frac{v}{3}
Un peso de 20 lb suspendido del extremo de un resorte vertical lo estira 6 pulgadas. Suponiendo que no haya fuerzas externas, encuentre la posición del peso en cualquier momento si inicialmente el peso se baja 2 pulgadas y se suelta. Encuentra el período y la amplitud.
Ecuación:
\frac{d^2y}{dt^2}+64y=0
Solución:
y=frac{1}{4}\cos8t+\frac{1}{4}\sin8t=\frac{\sqrt{2}}{4}\sin(8t+\frac{\pi}{4})
Período y amplitud:
Aproximadamente 0.35 ft y π/4 seg.
La ecuación
\frac{d^2I}{dt^2}+2\frac{dI}{dt}-3I=2\cost - 4\sint
tiene por solución
I=c_1e^t+c_2e^{-t}+\sint
, ¿cuál es la solución particular bajo las condiciones iniciales I(0)=2, I'(0)=-5?
I=2e^{-3t}+\sint
Halle el factor de integración de la ecuación
(x^3+xy^2-y)dx+xdy=0
y resuélvala.
\mu=\frac{1}{x^2+y^2}
y esto conduce a la solución
\frac{x^2}{2}+\tan^{-1}\frac{y}{x}=c
Resuelva la ecuación
y''+2y'=4x
y=x^2-x+Ae^{-2x}+B
Resuelva la EDO
(D+2)^2(D-3)^4(D^2+2D+5)y=0
y=(c_1+c_2x+c_3x^2)e^{-2x}+(c_4+c_5x+c_6x^2+c_7x^3)e^{3x}+e^{-x}(c_8\cos2x+c_9\sin2x)
¿Cuál es la solucioón de la EDO
y''(t)+y(t)=1
con condiciones en el origen y(0)=1, y'(0)=0?
1.
Obtenga esta solución con la transformada de Laplace.
Encuentre la transformada de Laplace de la siguiente función definida por trozos:
si 0<t<2 f(t)=1,
si 2<t<4 f(t)=-1,
si t>=4 f(t)=0
F(s)=\frac{3-4e^{-2s}+e^{-4s}}{s}
Encuentre la transformada inversa de Laplace de la función
F(s)=\frac{se^{-2s}}{s^2+16}
f(t)=H(t-2)\cos4(t-2)
Una resistencia de R = 10 ohmios, un inductor de L = 2 henries y una batería de E voltios están conectados en serie con un interruptor S. En t = 0, el interruptor está cerrado y la corriente I = 0. Encuentre I para t> 0 si E=20e^{-3t}.
I=5(e^{-3t}-e^{-5t})
Un inductor de 2 henries, una resistencia de 16 ohmios y un condensador de 0.02 faradios están conectados en serie con una batería de E = 100sin3t. En t = 0, la carga en el condensador y la corriente en el circuito son cero. Encuentre la corriente transitoria del circuito.
I(t)=-\frac{25}{52}e^{-4t}(17\sin3t+6\cos3t)
Si nos muestran un cubo vacío con un pequeño agujero en el fondo es imposible saber cuándo estaba lleno de agua hasta el borde. La ecuación diferencial para la altura h del agua viene dada por la ley de Torricelli:
\frac{dh}{dt}=-k\sqrt{h}
Este hecho es consecuencia de que no se satisface el teorema de existencia y unicidad.
¿Bajo qué cambio de variable, la ecuación
\frac{dx}{dt}=kx-x^2
se vuelve una ecuación lineal de variables separables?
u=\frac{1}{x}
Resuelva la ecuación
\frac{dy}{dx}=(x+y)^2
\arctan(x+y)=x+c
Resolver la EDO
(x^2D^2+xD-4)y=x^3
Es una ecuación de la forma Cauchy-Euler
y=c_1x^2+c_2x^{-2}+\frac{1}{5}x^3
Encuentre una solución particular de la ecuación
x''-x=e^{-t}\sine^{-t}+\cose^{-t}
x(t)=-e^t\sine^{-t}
Resuelva la Ecuación Diferencial
y^{(iv)}+2y''+y=\sin t
con condiciones en el origen y(0)=1, y'(0)=-2, y''(0)=3, y(iv)(0)=0.
y=(1+\frac{5}{8}t)\cost-(\frac{21}{8}-2t+\frac{1}{8}t^2)\sint
Resuelva el sistema de ecuaciones conformado por las siguientes ecuaciones diferenciales, sujeto a las condiciones iniciales x(0)=1, y(0)=0
x'(t)=2x-5y
y'(t)=x-2y
x(t)=\cost +2\sint
y(t)=\sint
¿Cuál es el tiempo de vaciado del agua a través de un orificio O de sección transversal a en el vértice?
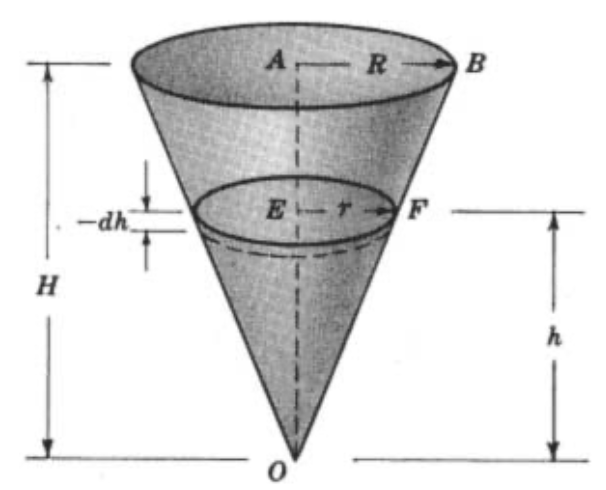
Suponga que la velocidad de salida es
v=k\sqrt{2gh}
, donde h es la altura instantánea del nivel del agua por encima de 0 y k es el coeficiente de vaciado.
Considerando la EDO
-\pi r^2 dh=av dt=ak\sqrt{2gh}dt
el tiempo de vaciado es
T=\frac{\pi R^2}{5ak}\sqrt{\frac{2H}{g}}
¿Cuál es el desplazamiento de fase del movimiento oscilatorio generado bajo las siguientes condiciones?
Un péndulo de masa m=2kg y de longitud 2.45 m está suspendido sobre un marco horizontal. El péndulo se levanta un ángulo de 10o y se suelta con una velocidad angular de -0.4 rad/seg.
NOTA: use la forma alternativa de la solución encontrada.
\theta(t)=\frac{\pi}{18}\cos2t-\frac{1}{5}\sin2t=A\sin(\omega t+\phi)
\phi\approx2.42 rad
¿La ecuación
y'=y^{1/3}
, viola el principio de unicidad de la solución? Muéstrelo.
Sí, tiene al menos dos soluciones:
y=0, \forall x
y
y=(\frac{2}{3}x)^{1/3}, x\geq0
Use la forma general de la ecuación lineal de primer orden para mostrar la solución de la ecuación
x\frac{dy}{dx}-2y=x^3\cos4x
y=\frac{1}{4}x^2\sin4x+cx^2
Indique qué haría para resolver la siguiente ecuación
(y')^2+2y=1
Derivar la ecuación.
(D^5-3D^4+3D^3-D^2)y=x^2+2x+3e^x
y=c_1+c_2x+(c_3+c_4x+c_5x^2)e^x+\frac{1}{2}x^3e^x-\frac{1}{12}x^4-\frac{4}{3}x^3-9x^2
Resuelva la ecuación diferencial
y''-3y'+2y=2e^{-t}
con condiciones en el origen, tales que y(0)=2, y'(0)=-1.
Usando la transformada de Laplace
y=\frac{1}{3}e^{-t}+4e^t+\frac{7}{3}e^{2t}
Halle la transformada de Laplace de la función definida por partes:
f(t)= sin t, si t<π
f(t)= t, si t>π
NOTA:use la función escalón unitario.
F(s)=\frac{1}{s^2+1}+e^{-\pi s}(\frac{\pi}{s}+\frac{1}{s^2}+\frac{1}{s^2+1})
Encuentre la transformada inversa de Laplace de la siguiente función
F(s)=ln(1+\frac{1}{s})
f(t)=\frac{1-e^{-t}}{t}
La sustancia química A se disuelve en solución a una velocidad proporcional a la cantidad instantánea de sustancia química no disuelta y a la diferencia de concentración entre la solución real Ca y la solución saturada Cs. Un sólido inerte poroso que contiene 10lb de A se agita con 100 galones de agua y después de una hora se disuelven 4 lb de A. Si una solución saturada contiene 0.2 lb de A por galón, encuentre la cantidad de A que no se disuelve después de 2 h.
Sean x libras de A no disueltas después de t horas. Tenemos
\frac{dx}{dt}=kx(0.2-\frac{10-x}{100})
Cuya solución es
\frac{1}{10}\ln\frac{x}{x+10}=kt +C_1
En t=2 horas tendremos x=3.91 libras de A no disueltas.
Muestre que la EDO que modela el movimiento oscilatorio de un objeto parcialmente sumergido en agua, es lineal de segundo orden y no homogénea.
Al utilizar el principio de Arquímedes en combinación con la segunda ley de Newton se llega a una ecuación con las características señaladas.
x''+\frac{3g}{2h}x-\frac{1}{2}g=0
Suponga que h es la altura del objeto, g la gravedad y x(t) la posición de la superficie del objeto al nivel del agua.