(7.5/7.6)
(7.5/7.6)
(8.1/8.8)
(8.2)
(7.5/8.8)
(8.3/8.4)
Find all exact solutions on the interval 0 ≤ θ < 2π
2cos(θ) = 1
π/3, 5π/3
Assume A is opposite side a, B is opposite side b, and γ is opposite side c. Solve for the triangle. Round to one decimal.
b=4 c=5 y=85°
A= 42.5°
a= 3.4
B= 52.8°
Find the area of a triangle with sides of length 10 in, 8 in, and 13 in. Round to two decimals.
39.98 in²
Find 5u + 2v
u = 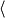 2, −5
2, −5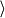 v =
v = 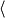 3, 2
3, 2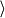
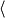 5, -3
5, -3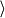
Convert the given polar coordinates to Cartesian coordinates (4, π/4)
(2√2, 2√2)
Find all solutions.
4 cos²(t) − 6 cos(t) = −2
0, π/3, 5π/3
Find the area of the triangle with the given measurements. Round to one decimal.
A=93° b=13 c=6
38.9 units²
Solve for side a to the nearest tenth
A=80° b=6 c=4
a=6.6
A boat is heading north at 110 MPH but there is a wind blowing northeast at 9 MPH. How many degrees off course will the boat be? Round to one decimal.
3.1°
Convert the given Cartesian coordinates to polar coordinates with r > 0, 0 ≤ θ ≤ 2π.
(4, 4)
(2√8, π/4)
Find the amplitude, period, and frequency of the function h(t) = 7sin(8πt)
Amplitude: 7
Period: 1/4
Frequency: 4
Given a vector with initial point (−8, 4) and terminal point (2, −1), find an equivalent vector whose initial point is (0, 0).
(10, -5)
Solve for angle A to one decimal.
a=9 b=13 c=18
A=28.3°
Solve for all solutions
1+cot2(x)=sec2
Does Not Exist
What is the name of the shape?

Cardiod
Sketch the graph below
y = 4cos(3x)

Given initial point (7, 1) and terminal point (0, 4), write the vector in terms of i and j.
-7i + 3j
Find the area of a triangle with sides of 6cm, 7cm, and 10cm.
33.4cm²
Find each solution in degrees.
cos2(x) - sin2(x) = 1/2
30°, 150°, 210°, 330°
Graph the polar equation.
r = 2 + 4 sin(θ)
