Parallel or Perpendicular Slopes
Parallel Lines cut by a transversal
Midpoint
Distance
Angles
100
True or False: Parallel lines always have the same slope
Answer: True
100
In the accompanying diagram, line n is parallel to
line m, line t is a transversal, and m∠1 = 24
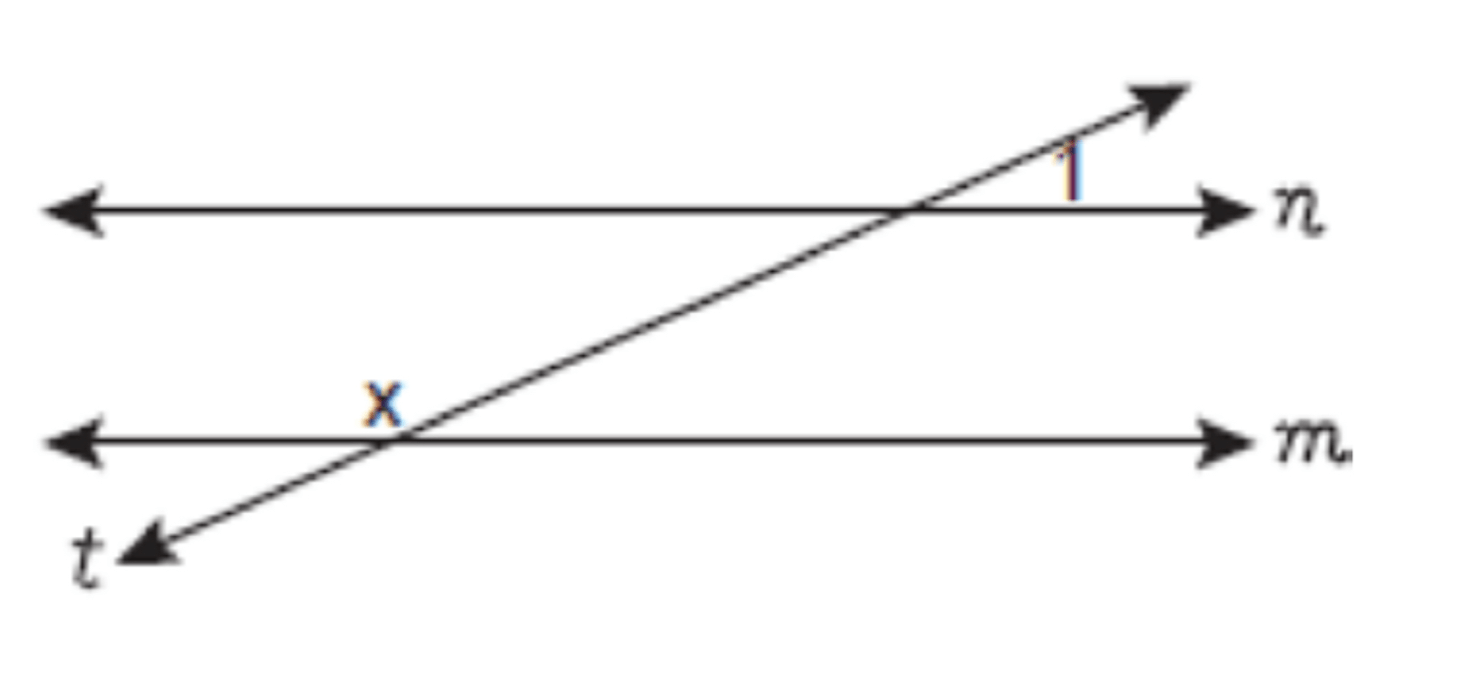
What does x equal, in degrees?
24
66
114
156
Answer: 3) 114
Angle 1 is suppplementary to the angle of x degrees
100
What are the coordinates of the midpoint of the line segment with endpoints (2, -5) and (8, 3)?
Mx = -1
100
What is the distance formula?
d=√(x2-x1)²+(y2-y1)²
100
Name 2 angles in this picture.
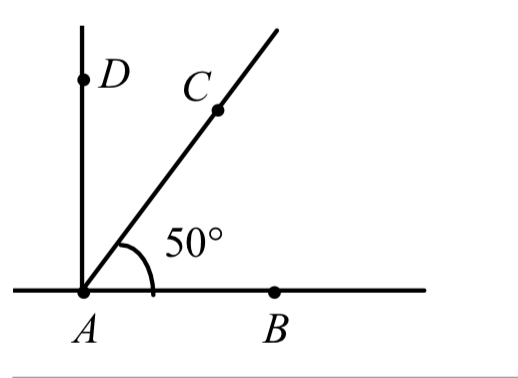
Answers: ∠DAB, ∠BAD, ∠DAC, ∠CAD, ∠BAC, ∠CAB
200
Which equation represents a line parallel to the x-axis?
1) x = 5
2) y = 10
3) x = 1/ 3 y
4) y = 5x + 17
2) y = 10
200
Transversal EF intersects AB and CD, as shown in the diagram below. Which statement could always be used to prove AB is parallel to CD?
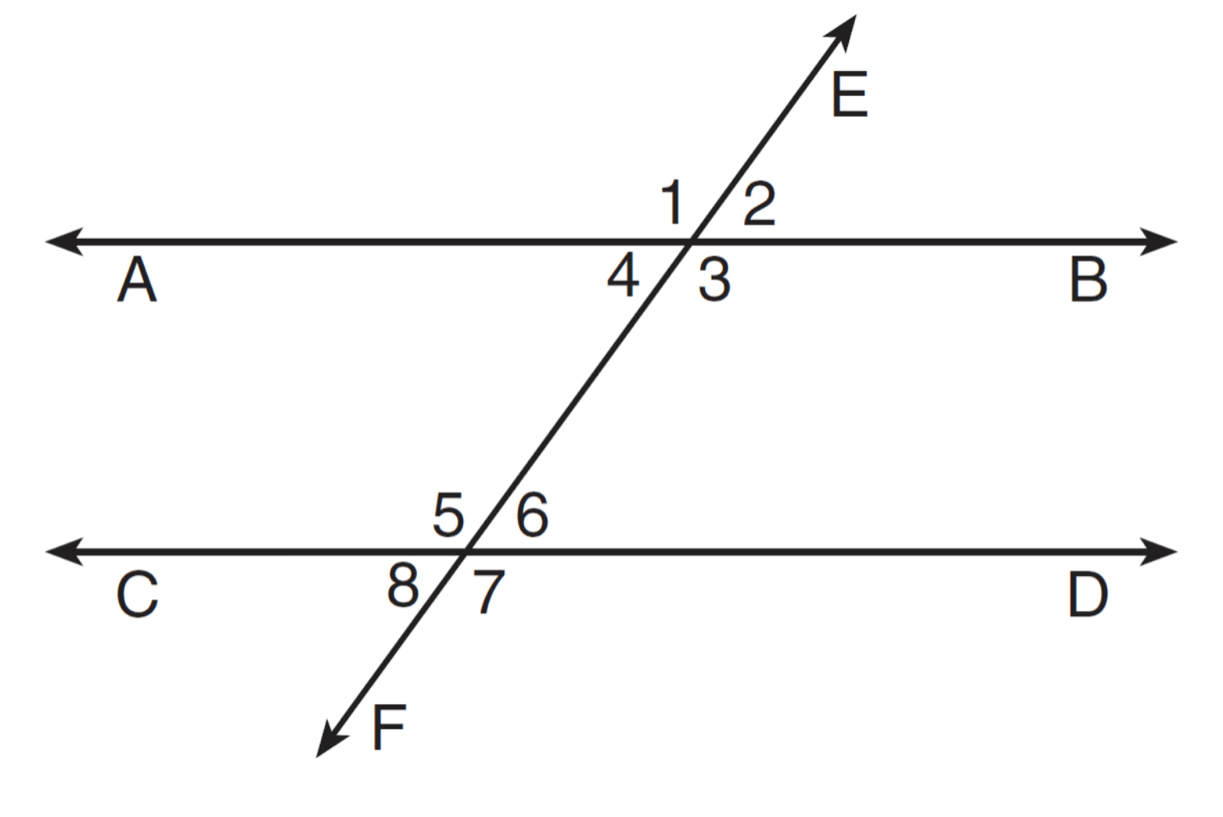
∠2 and ∠4 are congruent
∠7 and ∠8 are congruent
∠3 and ∠6 are supplementary
∠1 and ∠5 are supplementary
Answer: 3) 3 & 6 are supplementary- same side interior
200
A line segment has endpoints A(7, -1) and B(-3, 3). What are the coordinates of midpoint AB?
Mx = 1
200
Determine and state the length of a line segment whose endpoints are (6,4) and (−9,−4). In simplest form.
d = 17
200
Name two vertical angles and two supplementary angles in the diagram below.
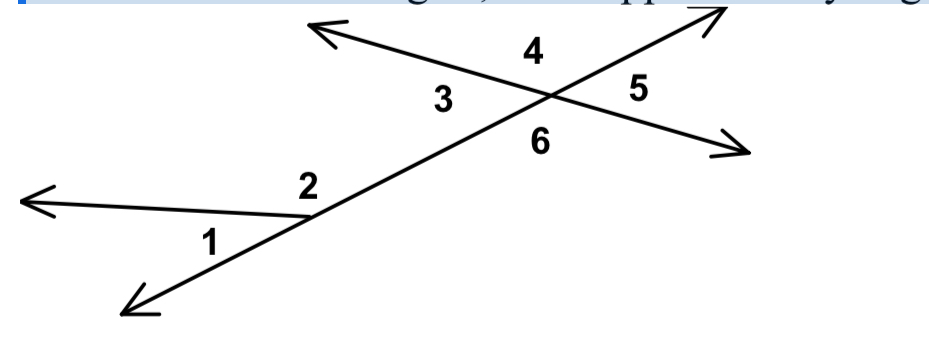
Vertical angles: 4 & 6, 5 & 3
Supplementary: 1 & 2, 3 & 4, 4 & 5, 5 & 6, 3 & 6
300
The slope of line l is -1/3. What is an equation of a line that is perpendicular to line l ?
Answer: 3
300
In the accompanying diagram, parallel lines AB and CD are intersected by transversal at points G and H, respectively, m∠AGH = x + 15, and m∠GHD = 2x.
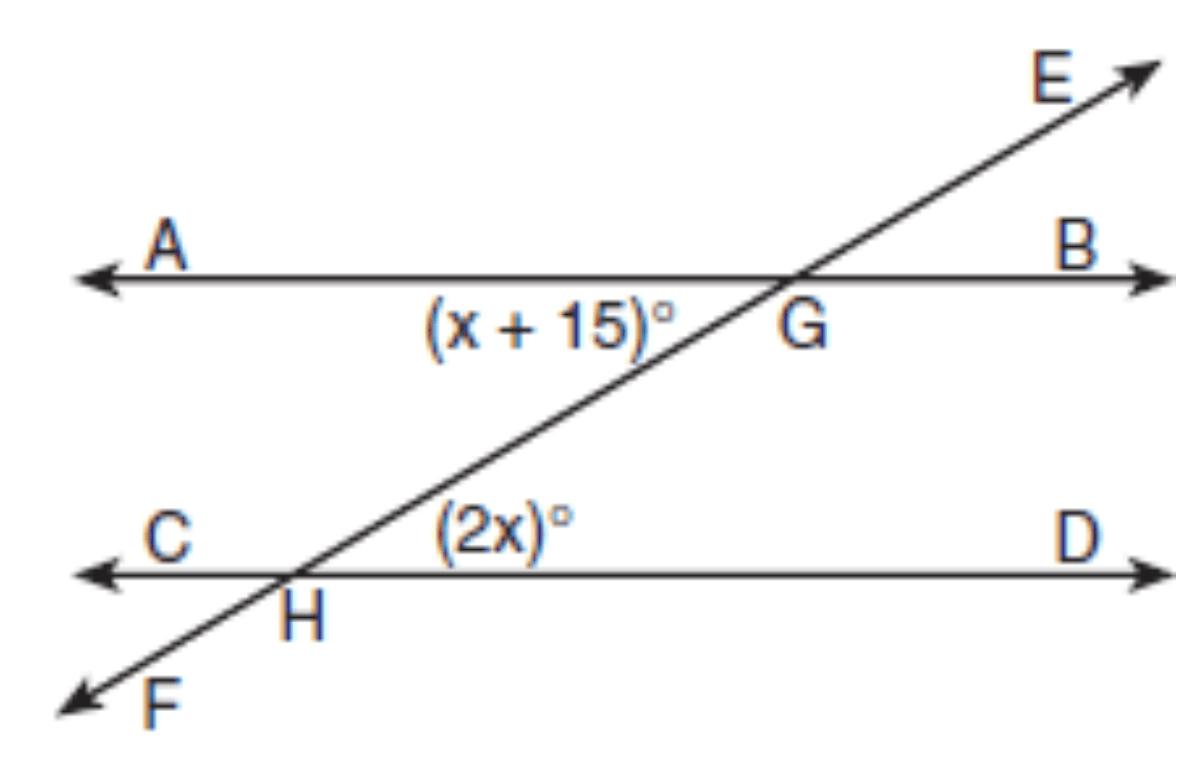
2x.
Which equation can be used to find the value of x? What angle relationship did we use to find it?
2x = x + 15
2x + x + 15 = 180
2x + x + 15 =90
2x(x + 15) = 0
1) 2x = x + 15
∠AGH and ∠GHD are congruent because they are alternate interior angles
300
A line segment on the coordinate plane has endpoints (2,4) and (4,y). The midpoint of the segment is point (3, 7). What is the value of y?
Yb = 10
300
The coordinates of the endpoints of CD are C(3,8) and D(6,−1). Find the length of CD in the simplest radical form.
d = 3√10
300
Which of the following is the value of x?
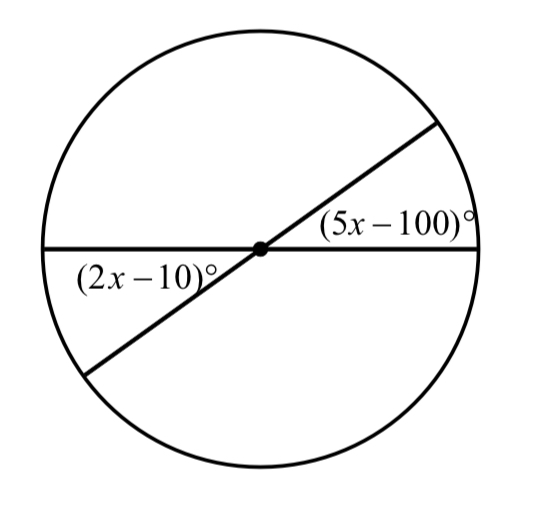
Answer: 30
400
What is an equation of the line that passes through the point (−2,1) and is parallel to the line whose equation is 4x − 2y = 8?
Answer: y = 2x + 5
400
Line n intersects lines l and m, forming the angles shown in the diagram below.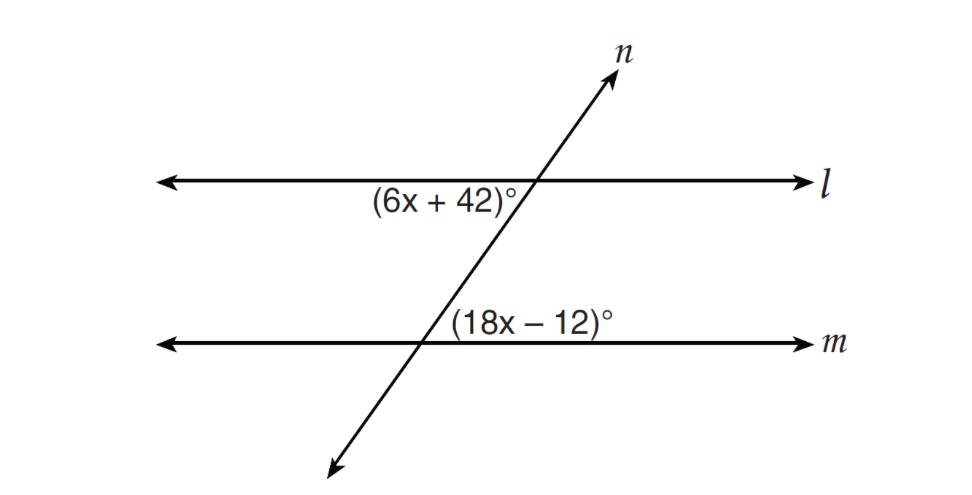
Which value of x would prove l and m are parallel?
2.5
4.5
6.25
8.75
Answer: 2) x = 4.5
400
If a line segment has endpoints A(3x + 5, 3y) and B(x - 1, -y), what are the coordinates of the midpoint of AB?
Mx = 2x + 2
MY= y
400
What is the length, to the nearest tenth, of the line segment joining the points (−4,2) and (146,52)?
d = √25,000≈ 158.1
400
The measures of two complementary angles are represented by (3x + 15) and (2x - 10). What is the value of x?
Answer: 17
The sum of complementary angles is 90 degrees.
500
An equation of the line that passes through (2,−1) and is parallel to the line 2y + 3x = 8 is?
Answer: y = −3/2 x + 2
500
In the diagram below, transversal TU intersects PQ and RS at V and W, respectively.
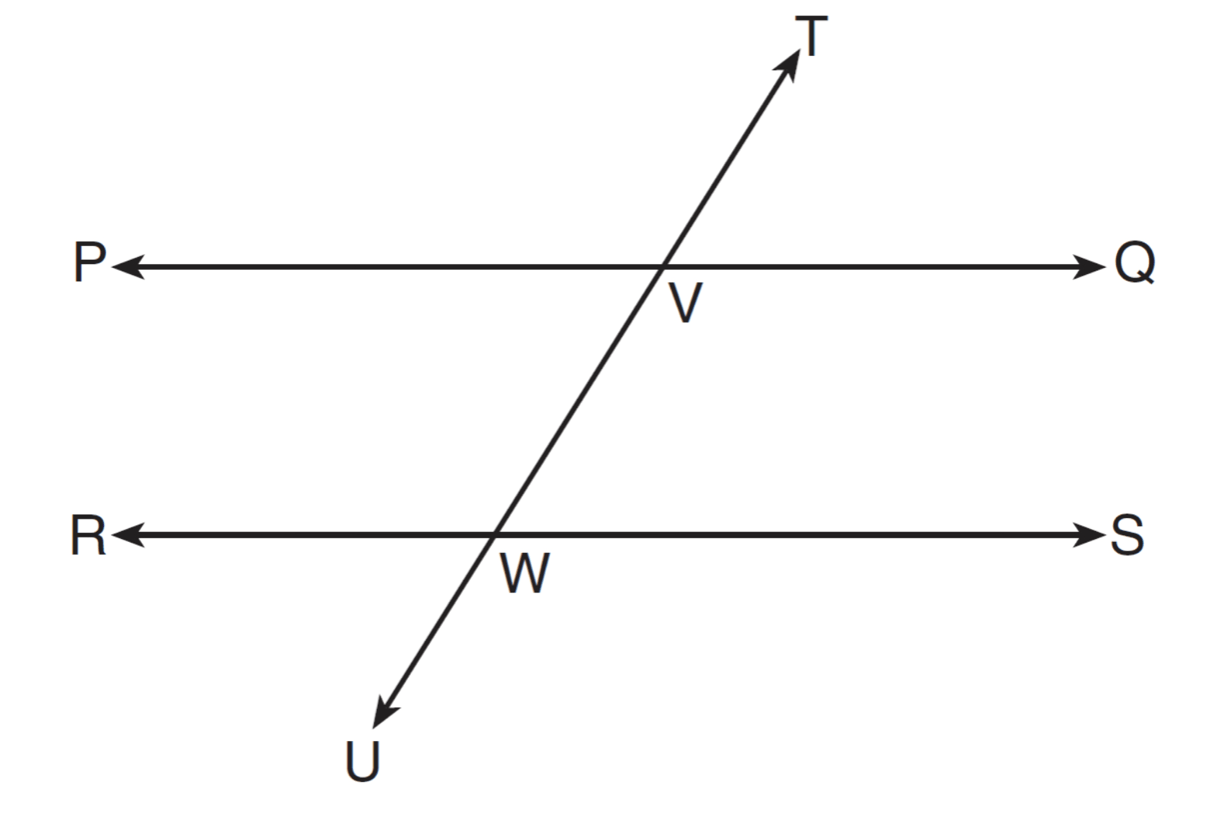
If and m∠TVQ = 5x - 22, and m∠VWS = 3x + 10, for which value of x is PQ parallel to RS?
x = 16
500
Point M is the midpoint of AB? If the coordinates of A are (-3,6) and the coordinates of M are (-5,2), what are the coordinates (x,y) of B?
x = -7
y = -2
500
The endpoints of AB are A(−4,5) and B(2,−5), what is the length of AB?
d = 2√34
500
In the diagram below, AB is parallel to CD. Transversal EF intersects AB and CD at G and H, respectively. If m∠AGH = 4x and m∠GHD = 3x + 40, what is the value of x? What angle relationship did you use to get your answer?
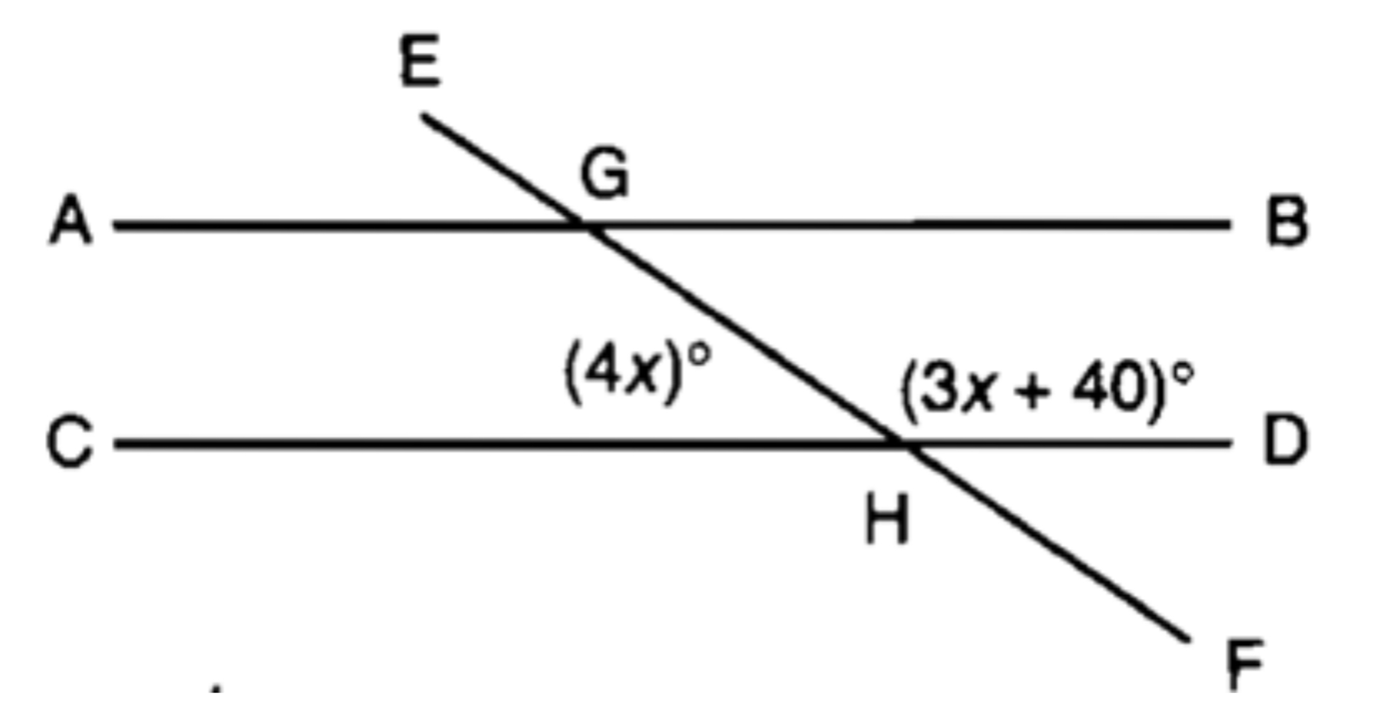
Answer : 20