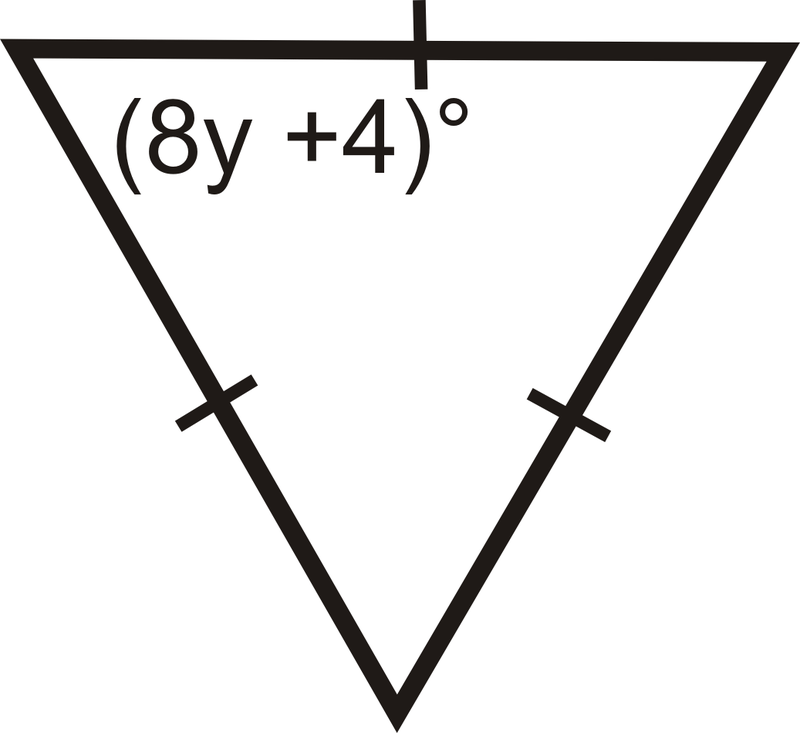Medians
Perpendicular Bisector
Isosceles/Equilateral
Angles of A Triangle
100
G is the centroid and AM is 18, find AG and GM.
AG = (2/3)AM
= (2/3)18
=2(6)
AG =12
AG + GM = AM
12 + GM = 18
GM = 6
100
Solve for x
x = 5
100
Solve for y
y = 7
100
Solve for x
x = 24
100
G is the centroid and OC = 30. Find OG and GC.
GC = (2/3)OC
= (2/3)30
=2(10)
GC =20
OG + GC = OC
OG + 20 = 30
OG = 10
100
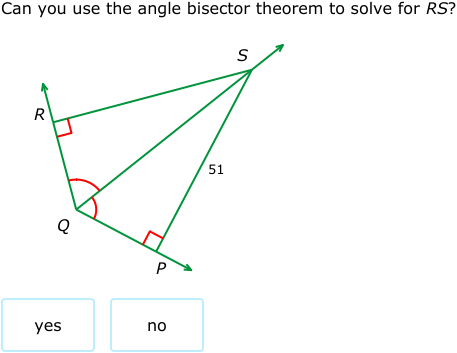
Yes, RS = 51
100
Find x, assume the triangle is isosceles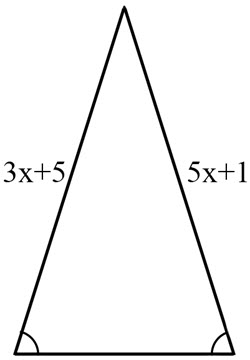
x = 2
100
Solve for x and find the exterior angle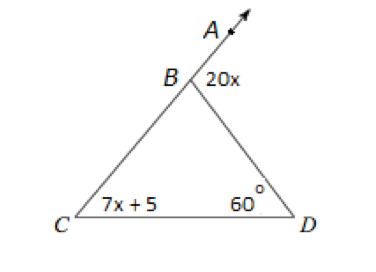
x = 5
200
G is the centroid and FG is 6 find GC.
GC = (2/3)FC
GC = (2/3)(FG + GC)
GC = (2/3)(15 + GC)
GC = 4 + (2/3)GC
(1/3)GC =4
GC = 12
200
Solve for x and find the length of DB and BC
x = 2, DB and BC = 9
200
Solve for y and find the vertex angle of the isosceles triangle
y = 16, Vertex Angle = 50
200
Find < A, <BCA, and < D.
<A = 86, <BCA = 82, and <D = 58
200
G is the centroid and EG is 10, find GB.
GB = (2/3)EB
GB = (2/3)(EG + GB)
GB = (2/3)(10 + GB)
GB = 20/3 + (2/3)GB
(1/3)GB = 20/3
GB = 20
200
Solve for x and find the length of AM and BM
x = 8, AM and BM = 16
200
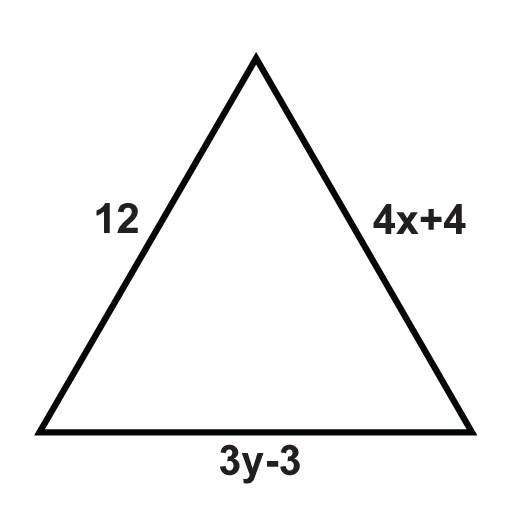
Solve for x and y, assume the triangle is equilateral
x = 2 and y = 5
200
Solve for <BAD and <B.
<BAD = 72 and <B = 52