Right Triangle Trig
Trig Ratios
Expressions
Use the Graph
Key Features
100
Convert 230o to a radian measure
(23pi)/18
100
Find the trig ratios for the given angles below:
sin((2pi)/3)
sin((2pi)/3)=(sqrt3)/2
100
Use the function to answer:
f(x)=-sin(3x)+4
f(pi/2)=
f(pi/2)=5
100
Find the range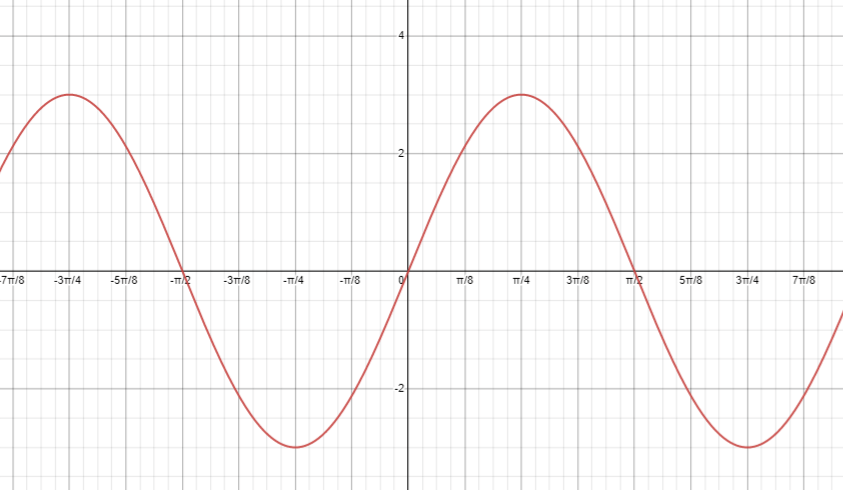 
Range :[-3,3]
100
Find the key features of the following function:
Midline, Amplitude, Period, Interval, Domain, Range
y=-cos(x/4)+3
Midline: y=3
Amplitude: 1
Period: 8pi
Interval: 2pi
Domain:(-inf,inf)
Range: [2,4]
200
Find the supplement of
pi/5
in radian measure
(4pi)/5
200
Find the trig ratio for the given angle
tan (210^o)
tan( 210^o)=(sqrt3)/3
200
Use the function to answer:
g(x)=4cos(x/2)-1
g(2pi)=?
g(2pi)=-5
200
What are the x-intercepts for the interval
-pi<=x<=pi
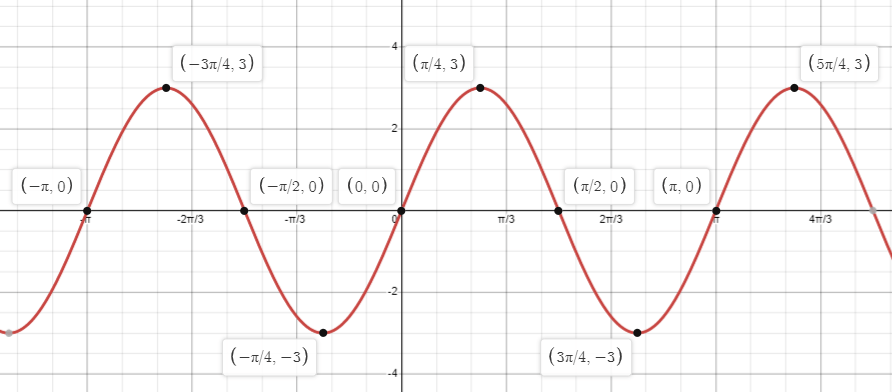
-pi, pi/2,0,pi/2, pi
200
Find the key features of the following function:
Midline, Amplitude, Period, Interval, Domain, Range
cos(3x-pi)
Midline: y=0
Amplitude: 1
Period: 2pi/3
Interval: pi/6
Domain: (-inf,inf)
Range: [-1,1]
300
Find two coterminal angles in radian (one positive, one negative) for angle
(5pi)/6
(17pi)/6,(-7pi)/6
300
Find the trig ratios for the given angles
sec(pi)
sec(pi)=-1
300
Use the functions to answer:
f(x)=-sin(3x)
g(x)=4cos(x/2)-1
g(f(pi))=?
g(f(pi))=3
300
Find the interval where the graph is positive for
-pi<=x<=pi
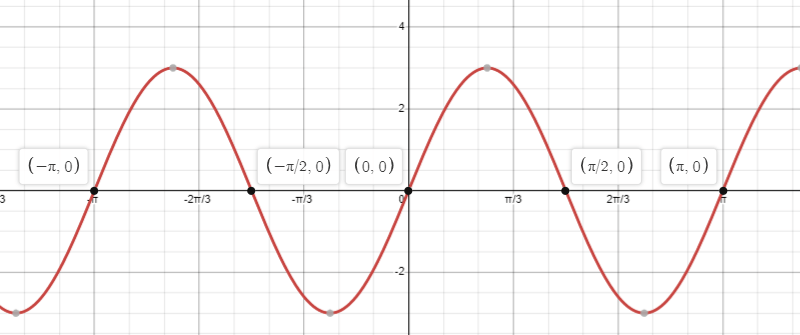
(-pi,-pi/2)U(0,pi/2)
300
Find the key features of following function:
y=-3cos(2x)
Midline, Amplitude, Period, Interval, Domain, Range
Midline: y=0
Amplitude:3
Period:pi
Interval:pi/4
Domain:(-inf,inf)
Range:[-3,3]
400
If
sin theta=4/7
and
theta
lies in quadrant 1, find the
costheta
in simplest form
costheta=(sqrt33)/7
400
Find x such that
0^o<=x<=360^o
sec(x)=(2sqrt3)/3
120^o,60^o
400
Given
f(x)=3cos(x)-1
complete for the given values:
400
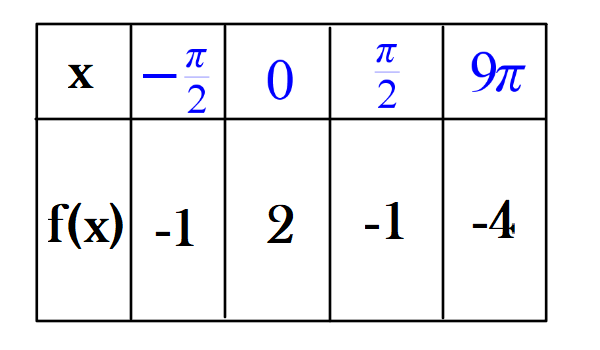
When is the function decreasing on the interval
-pi<=x<=pi
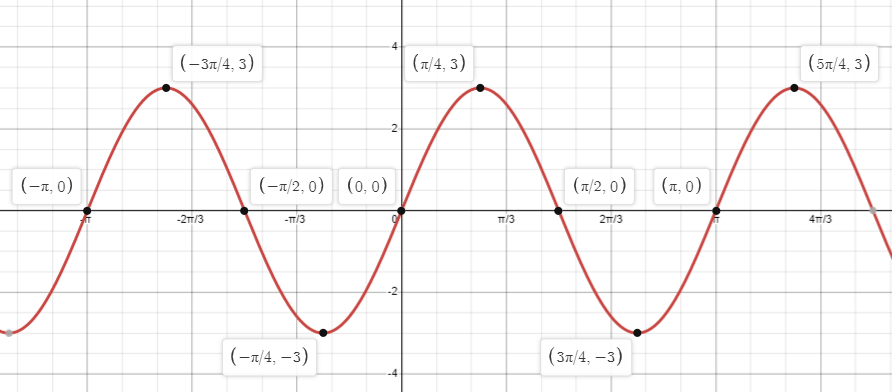
((-3pi)/4,-pi/4)U(pi/4,(3pi)/4)
400
Find the key features of the following function:
Midline, Amplitude, Period, Interval, Domain, Range
-sin(x/4)+2
Midline: y=2
Amplitude: 1
Period: 8pi
Interval: 2pi
Domain: (-inf,inf)
Range: [1,3]
500
Given
cos theta=4/5
theta and
sintheta<0
find
tan theta
tan theta=-3/4
500
Find x such that
0pi<=x<2pi
sin(x)=(-sqrt2)/2
(5pi)/4,(7pi)/4
500
Use the function to answer:
f(x)=-sin(3x)+4
f(pi/3)-f(0)
f(pi/3)-f(0)=0
500
When is the function increasing on the interval
-pi<=x<=pi
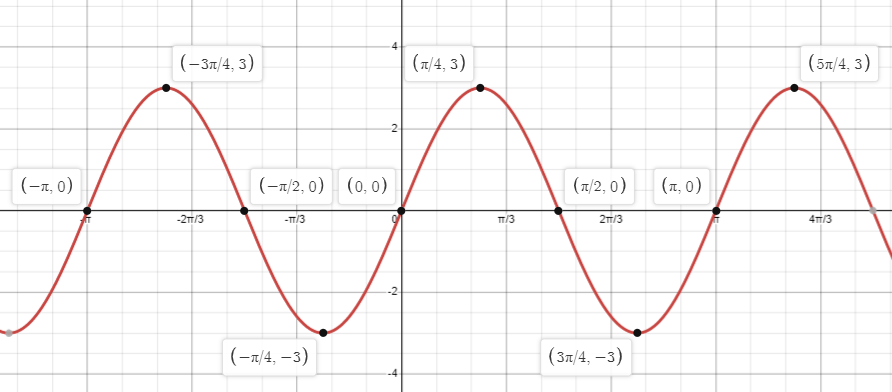
(-pi,(-3pi)/4)U(-pi/4,pi/4)U((3pi)/4,pi)
500
Find the key features of the following function:
Midline, Amplitude, Period, Interval, Domain, Range
1/3cos(2x-pi)+1
Midline: y=1
Amplitude: 1/3
Period: pi
Interval: pi/4
Domain: (-inf,inf)
Range: [2/3,4/3]