Rational Functions

Rational Arithmetic

250

(x-8)/(x^2-3x-40)\cdot(x^2-25)/(x+9)

(x-5)/(x+9)

500

(5x+4)/(x-3)

(5x+4)/(x-3)

x\ne3

750

x+3/(x+2) +(3x)/(x+5)

(x^3+10x^2+19x+15)/((x+2)(x+5))

1000

(x^2+4x-45)/(-x-4)\cdot(x+5)/(x^2+14x+45)\div(x^2-5x)/(-9)

9/(x(x+4))

Asymptotes/Holes

250

What is the horizontal asymptote of the function

 f(x)=-3/(x+2)+7 

y=7

500

What is the vertical asymptote of the function  f(x)=(2x)/(x(x-3)) 

x=3

750

Where is the removable discontinuity of this function  f(x)=(-5x+15)/(2x^2-18) 

(3, -5/12)

1000

What are the asymptotes and removable discontinuities of this function  f(x)=(4x^2+4x-48)/(-5x^2+45) 

VA at x=-3

HA at y=-4/5

RD at x=3

Domain/Range/End behavior

250

What is the domain of this function?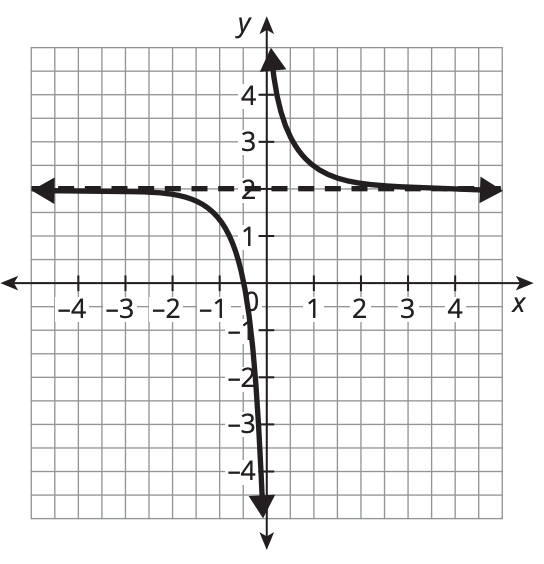

All real numbers except 0

500

What is the end behavior of this function?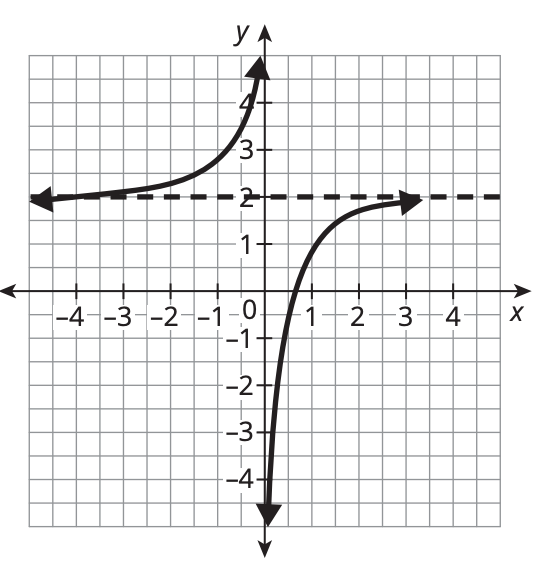

as x approaches infinity, f(x) approaches 2

as x approaches negative infinity, f(x) approaches 2

750

Range of this function 

f(x)=(-5x+10)/(x^2-3x+2)

All numbers except 0 and -5 

1000

Find the domain range and end behavior of this function

f(x)=(2x-3)/(3x+15)

Domain: all real numbers except -5

Range: all real numbers except 2/3

End Behavior: as x approaches infinity, f(x) approaches 2/3

as x approaches negative infinity, f(x) approaches 2/3