Organize these types of angles from smallest to biggest:
Right Angle
Acute Angle
Obtuse Angle
Acute Angle --> Right Angle --> Obtuse Angle
What type of angles are these?
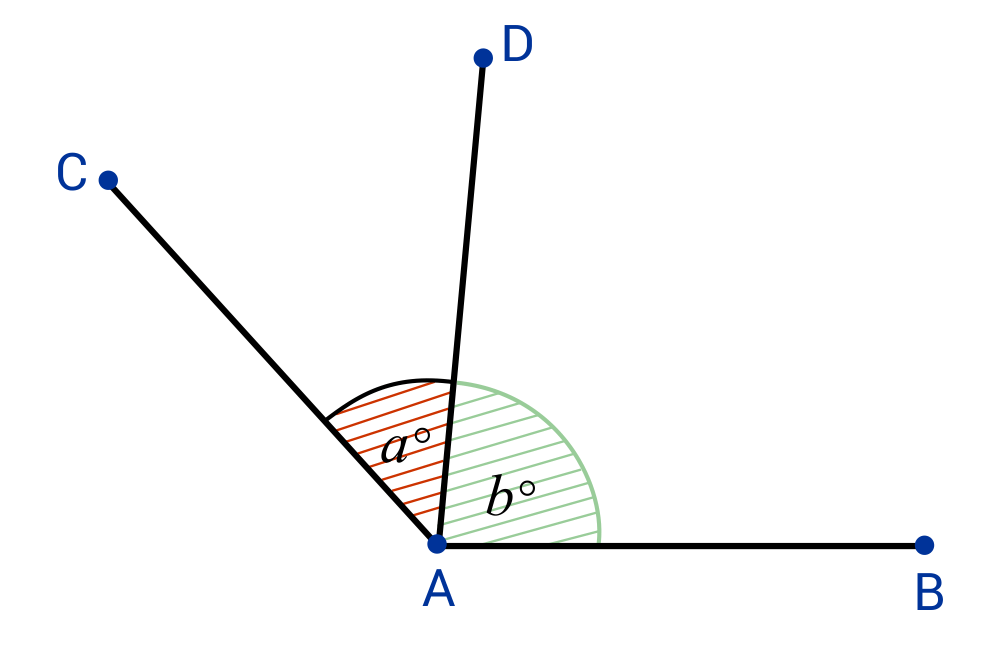
Adjacent Angles
Estimate the degree measure of this angle. Why?

Any obtuse angle measurement
Solve for the value of x

x = 16 Degrees
Identify the acute angle. Explain why
The 52 degree angle is acute because it is less than 90 degrees
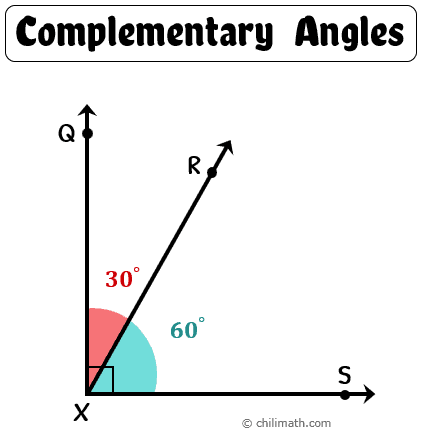
What makes two angles complementary?
Their measures add up to 90 degrees
Angles A and C are supplementary. Find the measure of angle C.

Angle C = 106 degrees
Solve for angles x and y
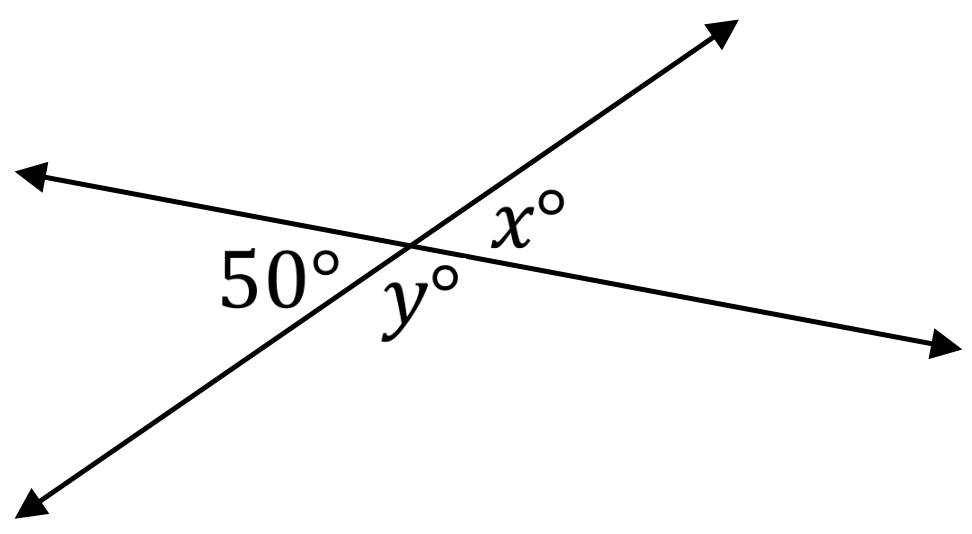
x = 50 degrees
y = 130 degrees
What is a straight angle?
An angle that is exactly 180 degrees
If two angles are supplementary, what do their measures add up to?
180 degrees
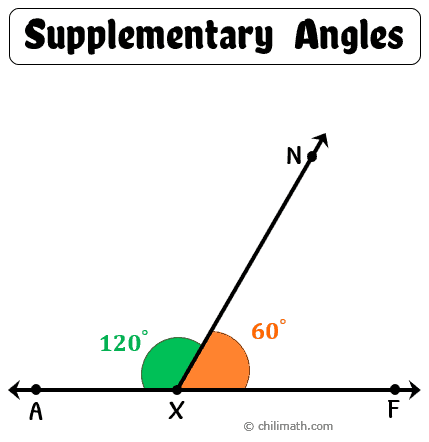
What are vertical angles?
Vertical angles are across the intersection point from one another. Vertical angle pairs have the same angle measurement.
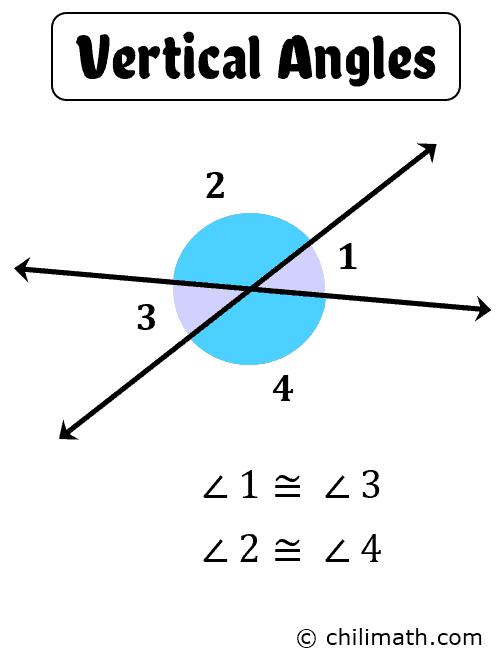
Solve for the value of g

g = 37 degrees
Where is the vertex in this picture?
Point B
What value for x completes these complementary angles?
x = 17 degrees
Find the value of b and c.

b = 42 degrees
c = 138 degrees
Write an equation to represent the relationship between the angles in this figure AND solve for b.

2b + 88 degrees = 180 degrees
b= 46 degrees
Figure out the degree measurement of the angle inside the hexagon.

120 degrees
What value for x completes these supplementary angles?

x = 62
Write 2 equations based on this picture.
y=76 degrees
x=z
y+x=180 degrees
y+z=180 degrees
x+76 degrees=180 degrees
z+76 degrees=180 degrees
Trevor thinks that this image has enough information to figure out the values of a and b. Is he right, why or why not?

No, a and b are not the same size.