Word Problems
Solutions
Mystery
Random review
100
Celia has 30 coins that total $4.80. All of her coins are dimes, D, and quarters, Q. Which system of equations models this situation?
A) D+Q=4.80
.10D +.25Q =30
B) D+Q=30
.10D +.25Q =4.80
C) D+Q=30
.25D +.10Q =4.80
D) D+Q=4.80
.25D +.10Q =30
B
100
What would you multiply the top equation by if you wanted to eliminate the "x" terms:
0.3x - 0.2y = -2.1
0.6x + 1.3y = 0.9
2 or -2
100
Find values for x and y that satisfy both equations
xy=72
x+y=17
8 & 9
100
Determine the measure of x and y
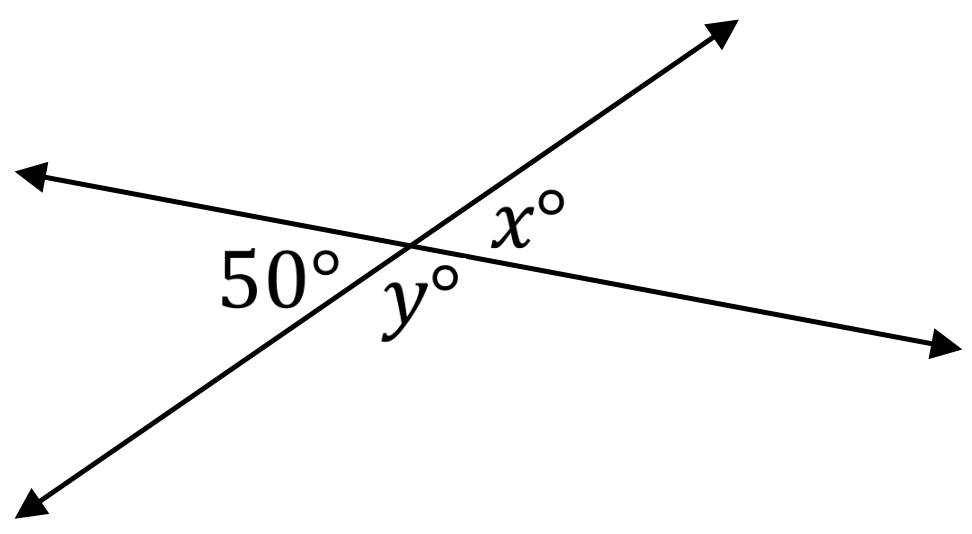
x=50, y=130
200
The sum of two numbers is 10. The difference of the same two numbers is 7. What are the two numbers?
8.5 and 1.5
200
If a+3b=13 and a+b=5, what is the value of b?
b = 4
200
What is the slope of the line between the points (-3, -5) and (6, -11)?
-2/3
200
What property is illustrated by the equation?
4(x+3) = 4(3+x)
Commutative
300
Cass spent $14.85 to buy 13 flowers. She bought lilies which cost $1.25 and tulips which cost $0.90 each. Write a system of equations to model this situation (be sure to define your variables!)
L = lilies, T = tulips
L + T = 13
1.25L + 0.90T = 14.85
300
What is the value of x in the solution of the system of equations?
3x+2y=12
5x−2y=4?
x=2
300
The total score in a football game was 72 points. The winning team scored 12 points more than the losing team. How many points did the winning team score?
42
300
What is the solution to the equation
15 - 2(w+5) = 11
w=-3
400
At an amusement park, the cost for an adult admission is a, and for a child the cost is c. For a group of six that included two children, the cost was $325.94. For a group of five that included three children, the cost was $256.95. Determine the price of each ticket.
c=46.99, a=57.99
400
Solve the following systems of equations:
3x+2y=4
4x+3y=7
x=-2, y=5
400
The angles in a triangle are represented as 3x - 8, 2x - 22, and 2x. Determine the measure of each angle in the triangle.
82, 60, and 38 degrees
400
Each day an elephant eats 5 pounds of food for every 100 pounds of its body weight. How much does a 9300 pound elephant eat per day?
465 pounds
500
The drama club is running a lemonade stand to raise money for its new production. A local grocery store donated cans of lemonade and bottles of water. Cans of lemonade sell for $2 each and bottles of water sell for $1.50 each. The club needs to raise $570 to cover the cost of renting costumes. The students will accept a total of 360 cans and bottles. Write a system of that can be used to represent this situation then solve it.
60 cans of lemonade, 300 bottles of water
500
Solve the following systems of equations:
−7x−4y=−4
−9x−y=−30
x=4, y=-6
500
Solve the system of equations:
7x+y=−3
−14x−2y=6
infinite solutions
500
To the nearest integer, find the volume of a cylinder with a diameter of 18 meters and a height of 3 meters.
763 cubic meters