Linear Equations
Exponential Equations
Quadratic Equations
Key Words
Functions
100
What does m represent in a slope-intercept formula
slope
100
A decay in an exponential function graph happens only when your common ration is less than this number
1
100
The quadratic equation in vertex form has these two variables representing your vertex
(h,k)
100
The turning point in a parabola
Vertex
100
This is slope-intercept form
y=mx+b
200
This variable represents the y-intercept in slope-intercept formula
b
200
The a0 variable in a Exponential Function represents
Initial value
200
The quadratic equation in standard form has this variable usually representing the y-intercept
(0,c)
200
The point where Y-axis is being intersected
Y-intercept
200
This is the quadratic equation vertex form
y=a(x-h)+k
300
When graphing the slope of a linear function we use this method to graph the m part (hint: its when we go vertically and horizontally)
rise/run or rise over run
300
The (b)x variable in a exponential function represents
common ratio
300
A parabola opens upwards automatically with this value
minimum
300
The shape of the graph of a quadratic function
Parabola
300
This is the quadratic function standard form
ax^2+bx+c
400
This other form for a linear function can be used to set up a slope-intercept form linear equation
point slope-form (y-y1)=m(x-x1)
400
This does not have a constant rate of change
Exponential Function
400
This vertex is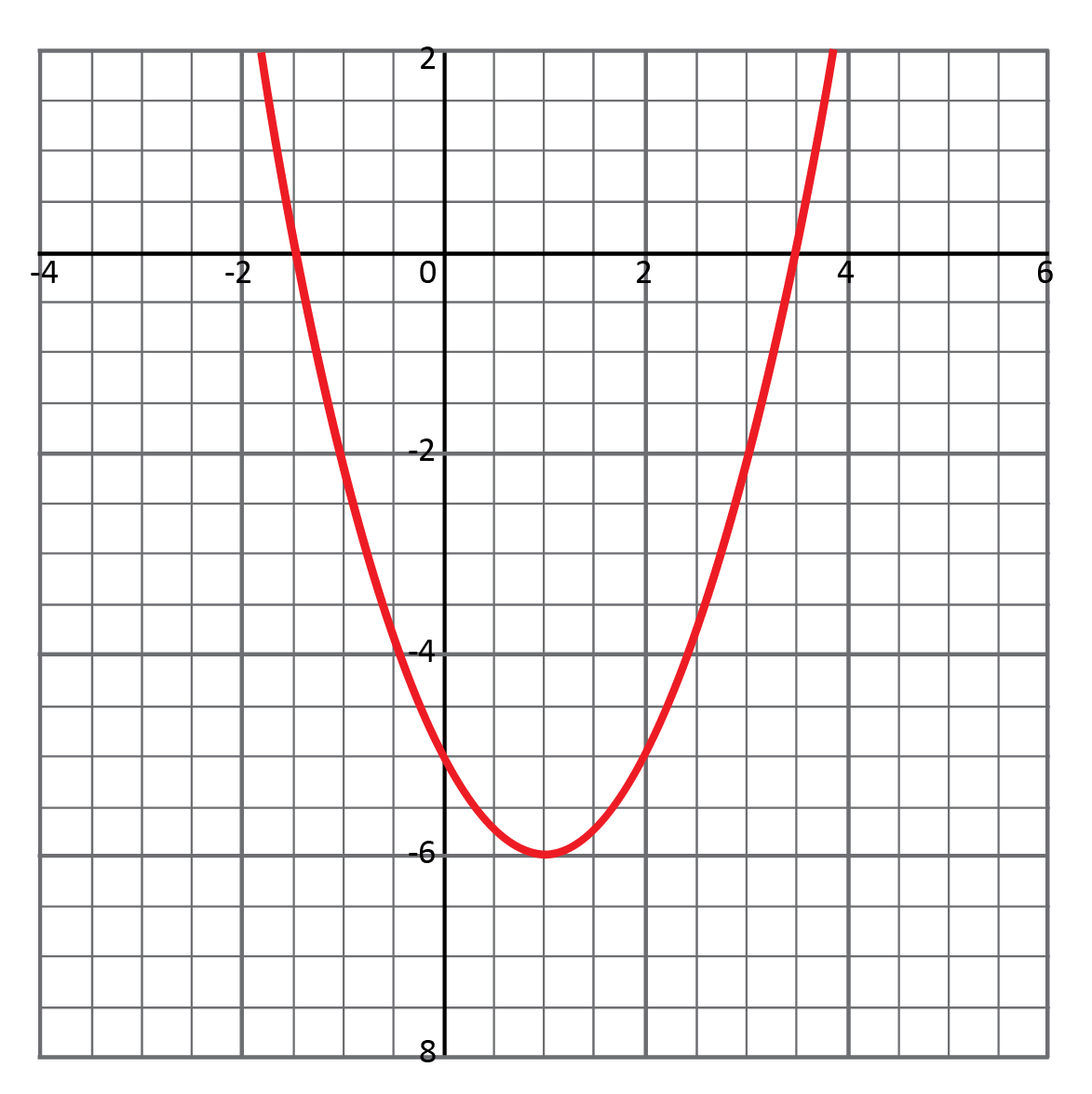 
(1,-6)
400
Is where the parabola is cut in half symmetrically
Axis of symmetry
400
The exponential function/equation
y=a0(b)^x
500
This (y=34x+25) linear functions slope is :
34
500
This part is never crossed or intersected in a exponential function graph
x-intercept
500
Is a second-degree polynomial equation
Quadratic function
500
The constant rate in a linear function
Slope
500
The x-coordinate of the vertex in a parabola can be found by using this formula
-b/2a