Given the function f(x) = 3x + 2 , evaluate f(4).
f(4) = 3(4) + 2 = 12 + 2 = 14
Solve the inequality 2x - 5 > 3
x>4
Graph:Open circle at x = 4, shaded to the right
Interval Notation: (4, ∞)
Simplify -7a2b – 2a2b.
-9a2b
What is the domain?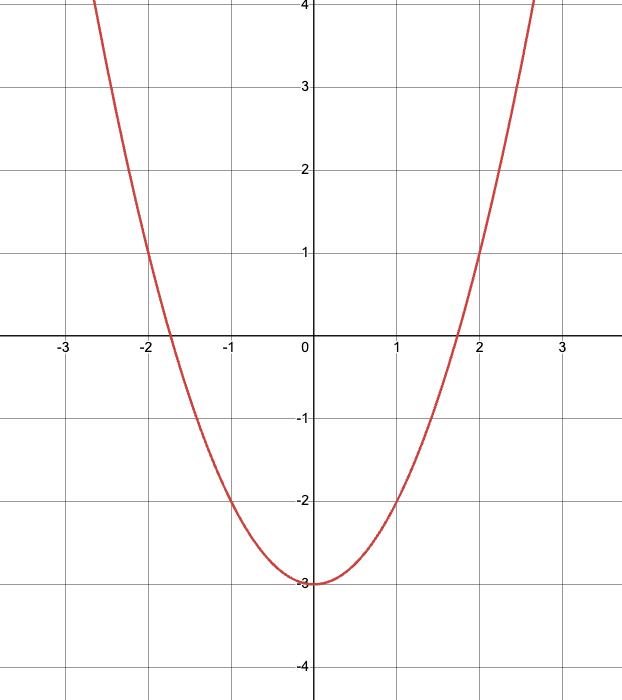
-∞<x<∞
(-∞,∞)
Write in logarithmic form: 82=64
log864=2
Given the function g(x) = x^2 - 4x + 5 , evaluate g(3).
g(3) = (3)^2 - 4(3) + 5 = 9 - 12 + 5 = 2 .
Solve the inequality 2x - 5 > x + 3
x>8
Graph: Open circle on 3, shaded to the right
Interval: (8, ∞)
Simplify (3x2y2)0
1
What is the range?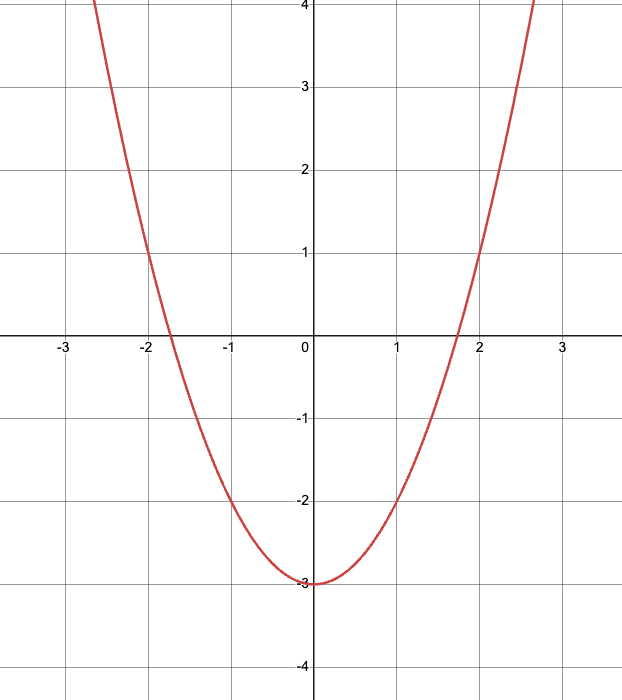
-3≤y<∞
[-3,∞)
x=2
Given the function h(x) =(2x + 1)/(x - 3) , evaluate h(5) .
h(5) = (2(5) + 1)/(5 - 3) = (10 + 1)/(2) = 11/2 = 5.5
Solve the inequality -2(x–5)≤4
x≥3
Graph: Closed circle on 3, shaded to the right
Interval: [3,∞)
Simplify (5ab)•(-2a2b)3
-40a7b4
What is the least possible degree of the polynomial function that produces this graph? Why?
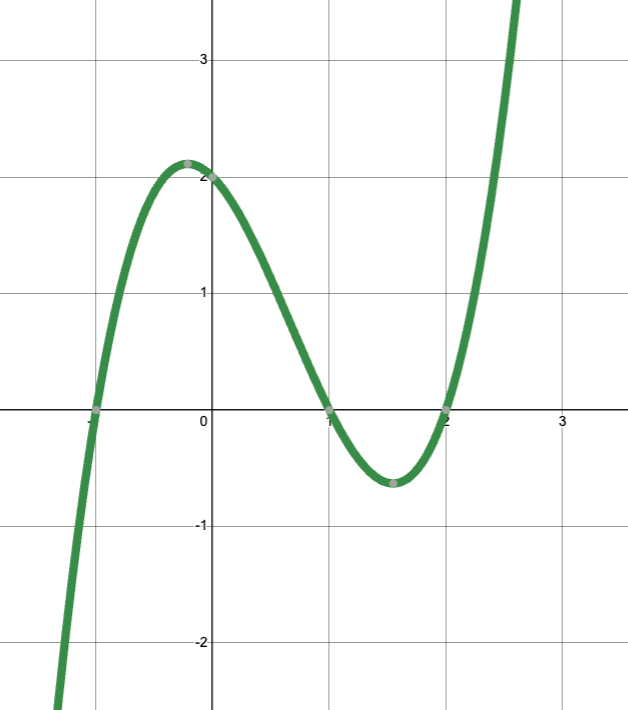
3, because there are 3 roots.
Condense: 3•log 2 + log(x – 4)
log(8x –32)
Given the functions f(x) = x2 + 1 and g(x) = √(x) , evaluate (f (g(4)) .
First, evaluate g(4) = √4 = 2 . Then, evaluate f(g(4)) = f(2) = (2)2 + 1 = 4 + 1 = 5 .
Solve the inequality 2(4x – 3) ≤ 5x – 27.
x≤ -7
Graph: closed circle on -7, shaded to the left.
Interval: (-∞,-7]
Solve: 53x-1•52x-5=5x+6
x=3
State the roots (or zeros) of the polynomial function in point form.
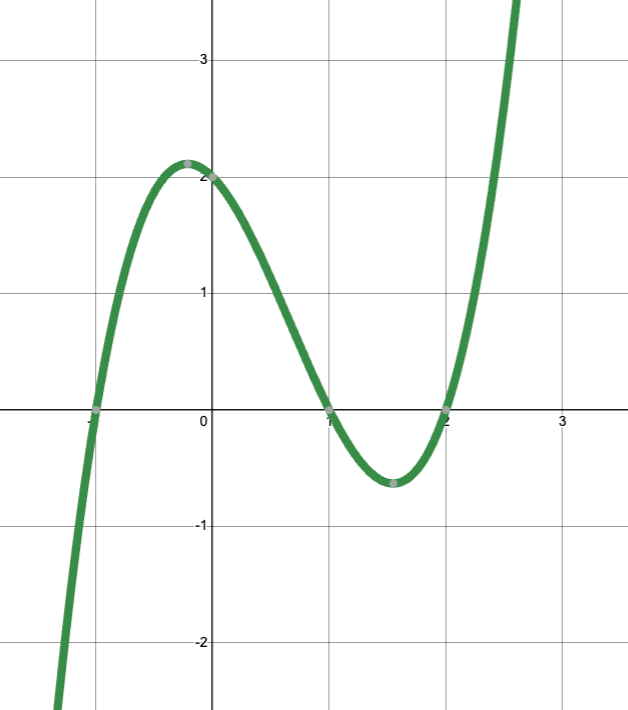
(-1,0), (1,0), and (2,0)
Solve: log4(5x+7)=log4(2x+31)
x=8
Given the functions f(x) = x2 + 1 , g(x) = √(x) , and h(x) = 3x + 2 , evaluate f(g(h(2)).
First, evaluate h(x) when x = 2, h(2) = 3(2) + 2 = 6 + 2 = 8.
Next, evaluate g(h(x)) = g(8): g(8) = √(8) = 2√(2).
Then, evaluate f(g(h(x))) = f(2√(2): f(2√(2)) = (2√2)^2 + 1 = 8 + 1 = 9
Solve the inequality: 4x + 7(3x –3)≤ 9 – 5x.
x≤1
Graph: Closed circle on 1, shaded to the left.
Interval: (-∞,1]
Solve: 32x+6•(1/2)=8x-1
x=-16
List all relative extrema for the function. Write your answers in point form. [You may have to estimate some points.]
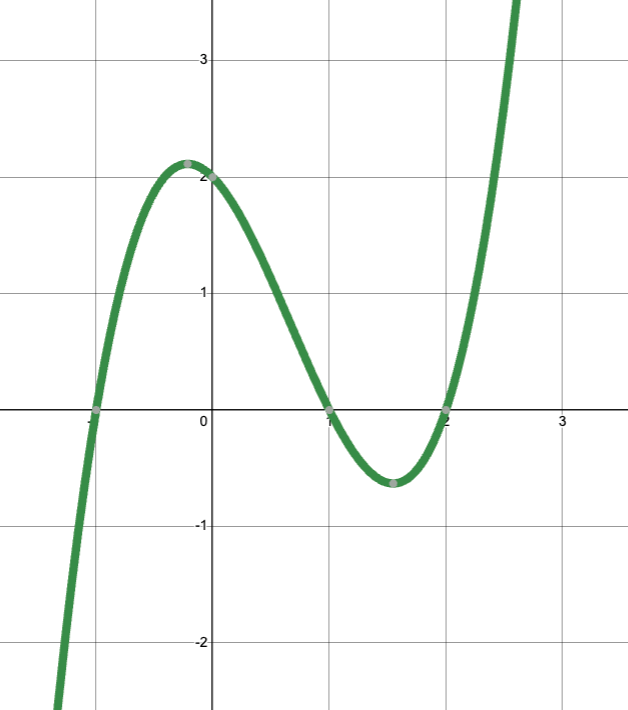
Relative max: (-0.2, 2.1)
Relative min: (1.5, -0.6)
Solve: log2(9m+2)=7
m=14