What type of transformation is the 2?
f(x) = |x|+2
Vertical Translation
f(x) = -2x-7
Find
f(3)
-13
Find the domain
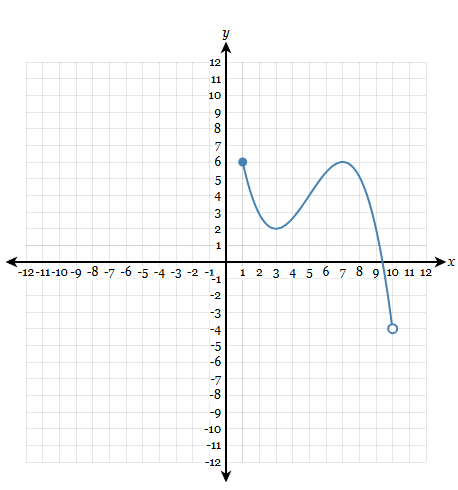
(-4,6]
Find f(7)
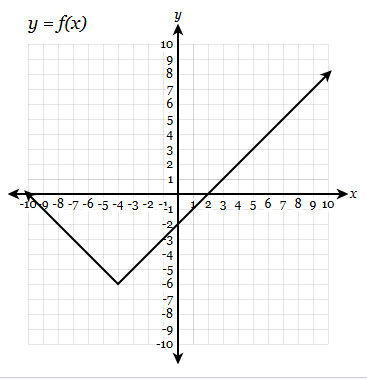
f(7) =5
What is the new location of the point (1,1) and (3,3) after the transformation below
f(x) = |x+3|
(-4,1) and (0,3)
Name Each transformation
f(x) = 3(x-4)2
3?
4?
3
Vertical Stretch
4
Horizontal Translation
f(x) = -5x-10
Find
f(x)=100
Find the range
[-6,4]
Find f(8)
f(8) = -4
What is the new location of the points (1,1) and (2,4) after the following transformation
f(x) = 2x2
(1,2) and (2,8)
Name Each transformation
f(x) = 2(-x)3
f(x) = -x2-2x+18
Find
f(-2)
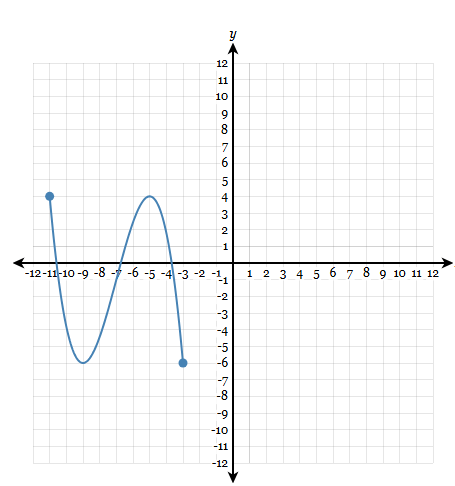
Find the Domain
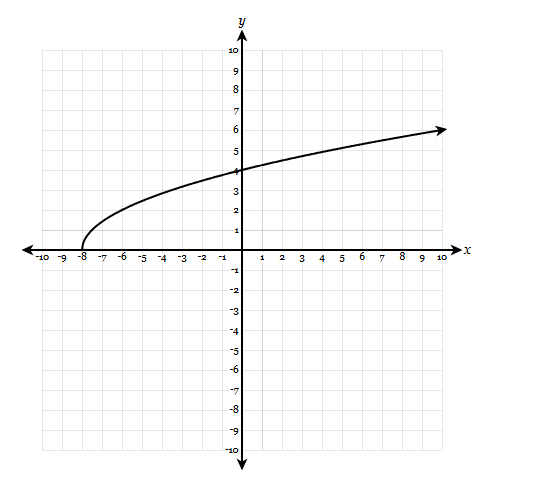
[-8,inf)
Find the value of f(x) =2
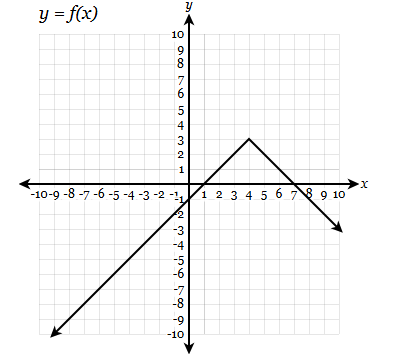
x=3,5
What is the new location of the points after the following transformations (-1,1) and (2,4)
f(x) = -(x+2)2
(-3,-1) and (0,-4)
Name Each transformation
3*2^(x-1)
Veritcal Reflection and Horizontal Stretch
g(x) =-8x3-2x2-3x-7
Find f(-3)
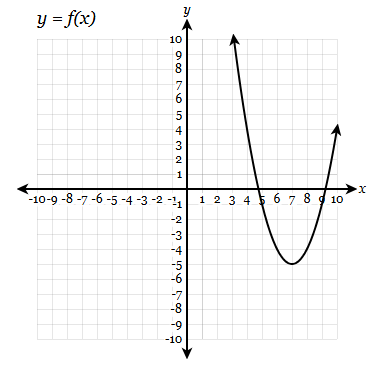
Find the range
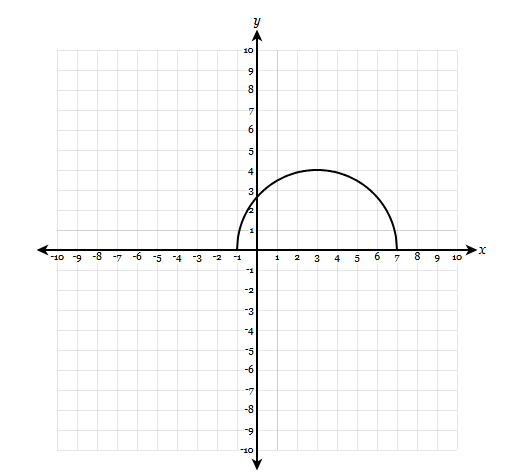
[0,4]
Find f(x) = 7
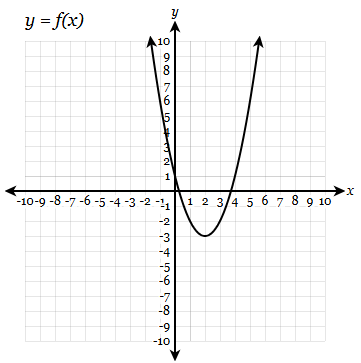
x=2,6
What is the new location of the points (-2,2) and (-4,4) after the following transformations
f(x) = -|1/3x|+2
(-6,0) and (-12,-2)
Name Each Transformation
-2*5^x-1
Vertical Compression and horizontal Compression
Find the missing input
h(x) = (3x-1)/(5x-3)
h(X)= 7
29
Find the range
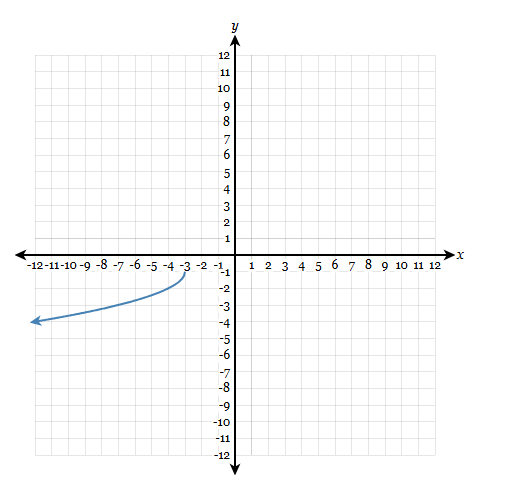
(-inf,-1]
f(3)
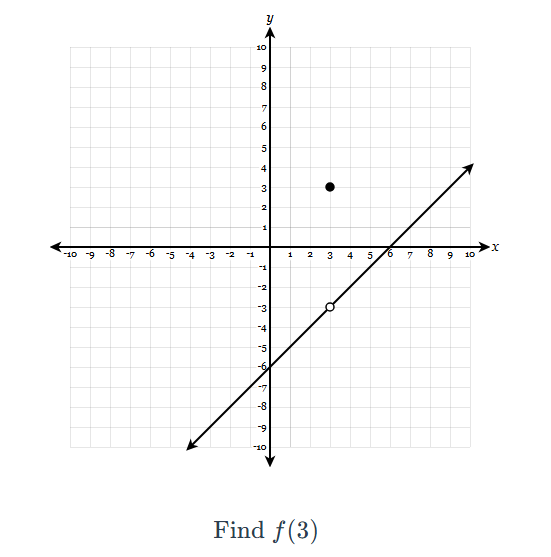
f(3) = 3
What is the new location of the points after the following transformations (-3,3) and (6,6)
f(x) = -2|3x|-10
(-1,-16) and (2,-22)