Rectangular Prisms
Triangular Prisms
Cylinders
Real-Life Applications
Challenge Questions
100
What is the formula for the surface area of a rectangular prism?
SA = 2L x 2W x 2H or SA = 2(L x W x H)
100
What is the formula for the surface area of a triangular prism?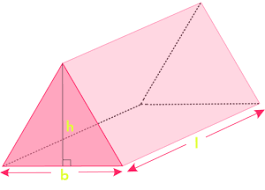
SA = 3(b x l) + 2(0.5 x b x h)
Explained =
Step 1: Find the area of the rectangles (rectangle = LW), multiply by 3 sides
Step 2: Find the area of the triangles (triangle = 1/2bh), multiply by 2 sides
Step 3: Add them all together
100
What is the formula for the surface area of a cylinder?
SA = 2pir^2 + 2pirh
100
What is one real-world example of a prism?
ice cube, tent, can, etc
100
What is the relationship between the dimensions and surface area?
surface area equals the dimensions squared
200
Find the surface area of a rectangular prism with dimensions 5 m, 3 m, and 7.9 m.
SA = l x w x h
SA = 5m x 3m x 7.9m
SA = 118.5m^2
200
Calculate the surface area of a triangular prism with a base of 5 ft, height of 4 ft, and length of 5 ft.
SA = 3(b x l) + 2(1/2 x b x h)
SA = 2(5ft x 5ft) + (5 x 4)
SA = 2(25ft) + (20ft)
SA = 50ft2 + 20ft2
SA = 70ft2
200
Find the surface area of a cylinder with a radius of 2.75 cm and height of 12 cm.
SA = 2pir^2 + 2pirh
SA = 2pi(2.75)2 + 2pi(2.75)(12)
SA = 298.55553313 + 207.34511514
SA = 505.90064827
SA = 505.90cm2
200
If you increase all dimensions of a prism by 50%, how does the surface area change?
the surface area would increase by 100%
Ex. dimension/side = 2m original SA = 22 =4m2
New Dimension = 2m x 0.5 = 1m
New Dimension = 2m + 1m = 3m
New SA = 3m2 = 9m2
300
If ONLY the length is doubled, how does the surface area change?
The surface area would double.
Ex. 5m x 3m x 2m = 30m2
5m x 2 = 10m
10m x 3m x 2m = 60m
300
If the height of the triangular base is halved, how does the surface area change?
The surface area will be halved as well
300
Explain how the surface area changes if the radius is tripled.
The surface area will increase by a factor of 9.
Ex.
2pi(4)^2 + 2pi(4)(6)
631.65468167 + 150.79644737 = 782.45112904
2pi(12)^2 + 2pi(4)(6) = 5684.892135
5684.892135 / 9 = 631.65468167
300
Create a word problem involving the surface area of a cylinder.
wrapper on a bottle
400
A rectangular prism has a length of 10 cm, width of 4 cm, and height of 6 cm. What is its surface area?
SA = l x w x h
SA = 10cm x 4cm x 6cm
SA = 240cm2
400
A triangular prism has 2 triangular faces with a base of 6 cm and a height of 4 cm. The prism is 10 cm long.
What is the surface area of the prism?
Step 1: find area of triangles (x2)
SA = 6 x 4
SA = 24cm2
Step 2: find area of rectangles (x3)
SA = 6 x 10
SA = 60 x 3
SA = 180cm2
Step 3: add them together
Total SA = 24 + 180
Total SA = 204cm2
400
A cylinder has a diameter of 14 cm and a height of 10 cm. Calculate its surface area.
r = 1/2 diameter
r = 14/2
r = 7
SA = 2pi(7)^2 + 2pi(7)(10)
SA = 1934.4424626 + 439.8229715
SA = 2374.2654341
400
Explain the significance of surface area in environmental science, such as in pollution control.
large surface area helps with absorption of toxins
500
Calculate the surface area of a rectangular prism with dimensions 8 cm, 2 cm, and 4 cm.
SA = l x w x h
SA = 8cm x 2cm x 4cm
SA = 64cm2
500
If a cylinder has a height of 12.4 cm and a radius of 3 cm, what is the surface area?
SA = 2pir^2 + 2pirh
SA = 2pi(3)^2 + 2pi(3)(12.4)
SA = 355.30575844 + 233.73449343
SA = 589.04
500
Apply the concepts of surface area to a 3D model of your choice and explain your calculations.
