Exponential Functions
Logarithmic Functions
Solving Expo/Log
Basic Trig and Unit Circle
Trig Identities
100
Determine whether the function below is exponential growth or exponential decay, and find the percentage rate of change.
P(x)= 0.75(1.035)xWhat is a growth of 3.5%?
100
Evaluate log327.
What is 3?
100
Solve 4^x=64 .
What is x=3?
100
Find CS. Round to the nearest hundredth.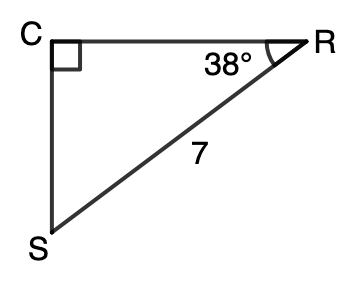 
What is 4.31?
100
Simplify the trigonometric expression.
cscxsinx.
What is 1?
200
The population of a colony of bacteria can be modeled by the function P(t)=25(1.042)t where P(t) represents the population and t represents time, in hours.
What does 25 represent in this function?
What is the initial population?
200
Evaluate
log(1/10)
What is -1?
200
Solve log_2x=6 ?
What is x = 64?
200
Find m\angle W . Round to two decimal places.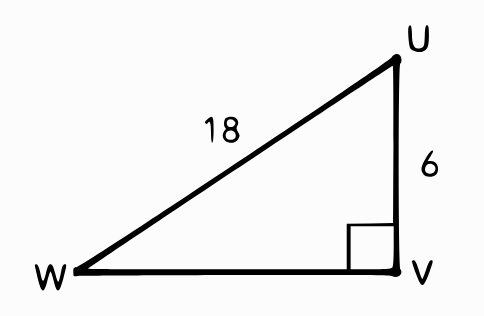 
What is
19.47^∘?
200
Simplify the trigonometric expression into one number or a single trigonometric function.
cscx⋅sin^2x
What is
sinx?
300
$10,000 is placed into an account earning an annual interest rate of 2.3%. To the nearest cent, find the value of the account after 5 years if interest is compounded weekly.
What is $11,218.45?
300
Rewrite the following logarithmic equations in exponential form.
logba=7
What is b7=a?
300
Solve e^x=60 . Round to the nearest thousandth.
What is x = 4.094?
300
Evaluate sin 45∘.
What is
sqrt2/2?
300
Simplify each trig expression into one number or an expression with a single trig function.
1-\sin^2 x - \cos^2 x
What is 0?
400
If $850 are placed in an account earning 1.7% interest, compounded continuously, how much will be in the account after 10 years?
What is $1007.51?
400
Condense using log properties.
ln12−ln3
What is
ln4?
400
Solve -7+2\text{log}_3 x =-5
.
What is x = 3?
400
Evaluate Cos 0 .
What is 1?
400
Simplify the expression \cos x + \sin x \tan x.
What is sec x?
500
The amount of caffeine in a person’s body decreases about 15.3% every hour. Sarah drinks a cup of coffee with 95 milligrams (mg) of caffeine in it.
Write an equation for the function C that gives the amount of caffeine in her body C(t), in milligrams, after t hours.
What is C(t) = 95(0.847)t ?
500
Condense using log properties.
3log_5x−2log_5x
What is
log_5x?
500
Solve log(x^2+5)=\text{log} 21.
What is x=±4?
500
Evaluate tan ((-5\pi)/3 \).
What is
sqrt3?
500
Simplify the expression \frac{\cos^2x+\sin^2x}{1+\tan^2x}-\cos^2x
What is 0?