What is the slope of the table below?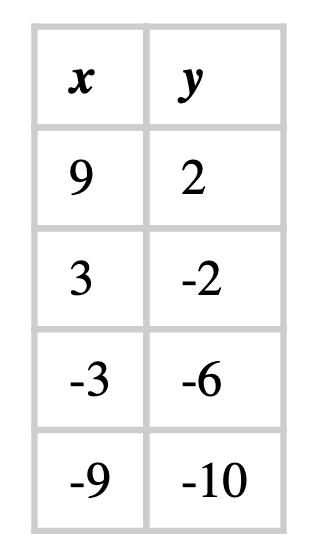
m= 2/3
What are the x & y intercepts of the following equation:
- 8x + 6y = 24
*write as ordered pairs
X-intercept: (−3,0)
Y-intercept: (0,4)
Identify the slope and point (x,y) in the equation:
y + 9 = -7(x - 4)
slope = -7
point = (-4,9)
List the equations for the following forms of linear functions:
1. Slope-intercept Form
2. Standard Form
3. Point-Slope Form
1. y=mx+b
2. ax+by=c
3. y-y1=m(x-x1)
Complete the sentences:
1. A linear function has a __________, and the line is ________.
2. A proportional line goes through the _______: (_,_).
3. A function can have repeating ____ values but not repeating _____ values.
1. A linear function has a CONSTANT ROC, and the line is STRAIGHT.
2. A proportional line goes through the ORIGIN: (0,0).
3. A function can have repeating Y values but not repeating X values.
Find the slope-intercept form of the line that passes through the points (2, 4) and (3, 7).
y=-2x+11
Find the Slope and y-intercept of the equation:
3x+9y=-5
y=-1/3x−9/5
slope=-1/3
y-intercept=-5/9
Write the equation (in point-slope form) of the line that passes through the points (3, 2) and (7, 6) using point-slope form.
y−2=1(x−3)
OR
y−6=1(x−7)
Your team got a free points!!
Go again
What is the Domain and Range of the graph?
Domain: [0, ∞)
Range:[40,∞)
A worker earns $12/hour and starts with a $50 bonus on their first paycheck.
Write an equation for their total pay y after x hours.
y=12x+50
Determine the ordered pairs that is a solution of the equation 15x-6y=-6.
a. (0, 1)
b. (2, 6)
c. (–2, –4)
d.(4, 12)
a. (0, 1)
b. (2, 6)
c. (–2, –4)
The slope of a line is 3, and the line passes through the point (4, -7).
Write an equation for the line in slope-intercept form.
y=3x−19
Nelson went to the Taste of Tacos, a festival where people come to taste a variety of tacos. The festival charges an admission fee to attend and then charges $3 per taco. By the end of the festival, Nelson spent a total, y, of $30 and purchased 6 tacos, x.
Write an equation using Slope-Intercept Form, Standard Form, or Point-Slope Form.
Point-Slope Form
y−30=3(x−6)
What kind of lines are on the graph? Write the equation for both.
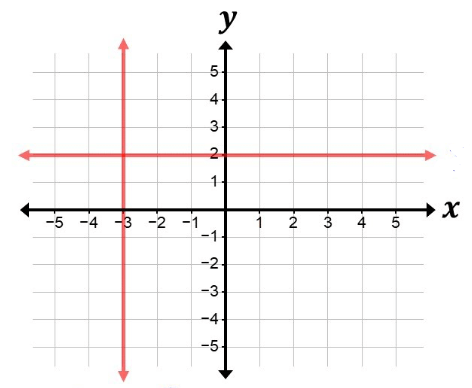
Horizontal line: y=2
Vertical (undefined) line: x= -3
What is the equation of the graph below?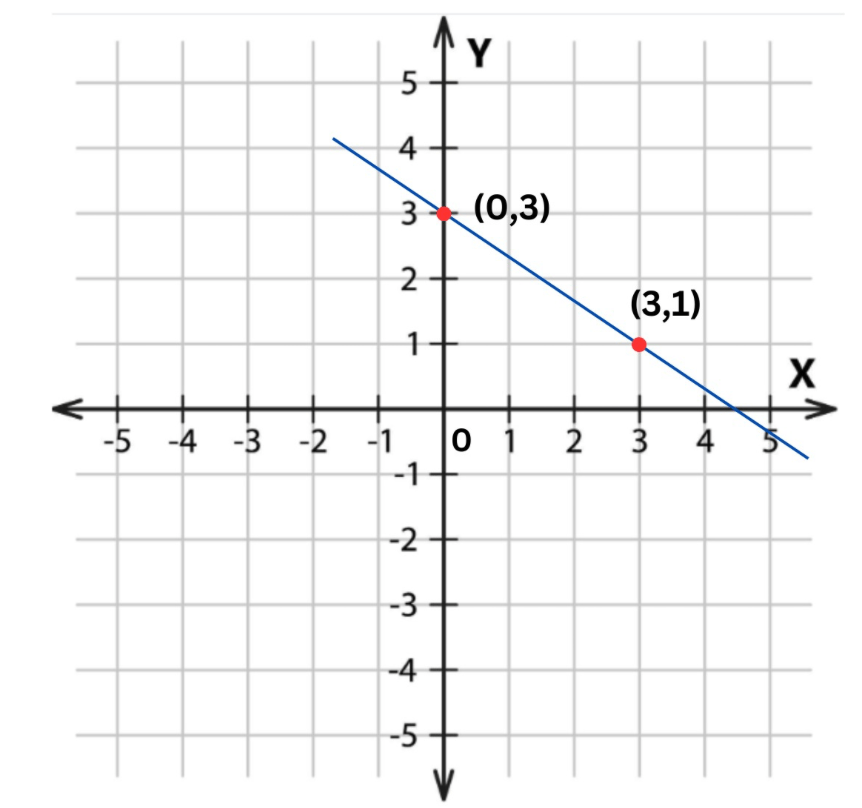
y=-2/3x+3
Jada has $24 to spend on games and rides at a carnival. Games cost $4 each, and rides are $6 each. She uses the equation 4x + 6y = 24 to represent the relationship between the number of games, x, and the number of rides, y, that Jada could do if she spends all of her money.
What’s the number of rides the student could get on if they don’t play any games?
4 rides
To complete a house repair, a contractor charges a flat fee for materials and $25 per hour for labor.
The total cost for 6 hours of work came to $275. After paying the bill, Maria wondered how much she spent on materials alone. Assume x represents the number of hours worked and y represents the total cost of the repair.
Write an equation in Point-Slope Form.
y−275=25(x−6)
A football team has an away game, and the bus breaks down. The coaches decide to drive the players to the game in cars, c, and vans, v. Four players can ride in each car. Six players can ride in each van. There are 48 players on the team.
Write an equation using Slope-Intercept Form, Standard Form, or Point-Slope Form.
Standard Form
4c+6v=48
What are the intervals of negative AND positive values of the graph below?
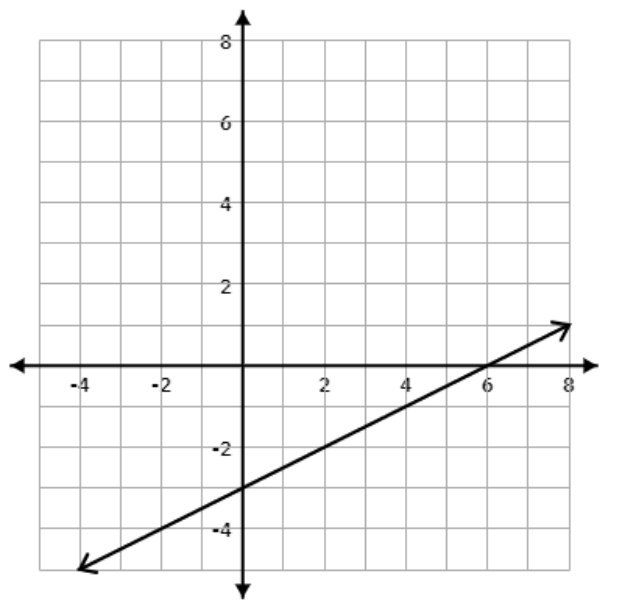
Interval of positive values: x>6 OR 6<x<∞
Interval of negative: x<6 Or -∞<x<6
John calls a plumber to fix a drain. He finds out that if the plumber worked 2 hours, the total cost was $130, and if he worked 5 hours, the total cost was $250.
1. Write the equation in slope-intercept form.
2. How many hours would the plumber have worked if the total was $200?
1. y=40x+50
2. 15/4 OR 3.75
Miguel has $30 to spend on snacks and tickets for rides. Each snack costs $5, and each ride ticket costs $3. Write an equation to represent all the combinations of snacks (x) and ride tickets (y) Miguel could buy if he spends all of his money.
5x+3y=30
The cost to rent a power drill was $30 on day 1 of a renovation. By day 11, the cost had dropped to $10. Let x represent the day of the renovation, and y represent the rental cost.
Write an equation in slope-intercept form.
y=−2x+32

Slope intercept form
y = 3x + 6
Complete the following operations without a calculator:
1. 146 + 385 =____
2. -15 - 7 =____
3. 63 * 4 =____
4. 5 / 4 =
1. 531
2. -22
3. 252
4. 1.25