What is the image point of (-8,9) after a translation left 3 units and down 5 units?
(-11,4)
Factor the expression completely:
(x-7)/(x-4)=5/x
x=10 and x=2
Name the solutions of the system of equations:
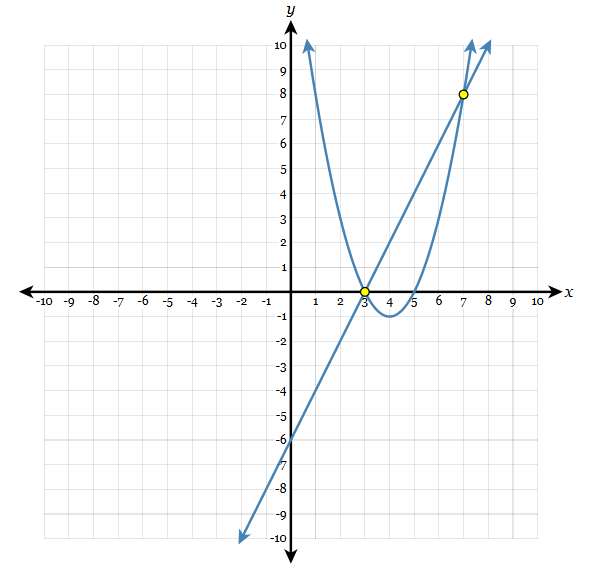
(3,0) and (7,8)
Simplify:
((8x^7y^-8z^2)/(-2x^4y^16z^8))^0
1
Simplify:
8sqrt(108)
48sqrt3
Name the image of the point (-6,-2) reflected over the x-axis, then the y-axis.
(6,2)
Factor the expression completely:
45a^2-80
5(3a-4)(3a+4)
Solve the system of equations. Write your answer as a coordinate point:
y=x^2+4x-3
y=x-3
(0,-3) and (-3,-6)
Simplify:
(20y^2)/(4y^5)^4
5/(64y^18)
sqrt(3x-15)-13=-10
x=8
Name the image of the point (1,-3) rotated 90 degrees clockwise.
(-3,-1)
Name the complete the square constant (hint: formula):
x^2+7x=-37
49/4
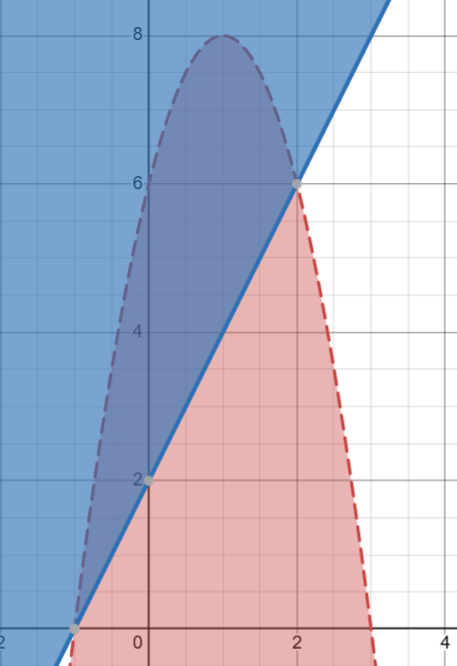
Name a solution to the system of inequalities:
y<-x^2+8x+7
y>=2x+2
Simplify:
x*x^(4/5)
x^(9/5)
Simplify completely:
6/sqrt(28)
(3sqrt7)/7
Name the transformations of the quadratic function:
y=3/2x^2+7
Convert the quadratic to vertex form:
y=2x^2-4x-4
y=2(x-1)^2-6
Solve the system of equations. Write your answer as a coordinate point:
y=sqrt(3x+16)
y=x+2
(3,5)
Simplify:
(64x^12)^(1/3)
4x^4
Solve:
sqrt(43-7x)=x-7
No Solution
Name the transformations of the function from its parent:
y=-3/(x+1)-2
Reflection over the x-axis
Vertical stretch of 3
Left 1
Down 2
Solve the equation using the quadratic formula (keep your answer as a simplified radical):
9x^2-24x=-19
(4+-isqrt(3))/3
Solve the system of equations. Write your answer as a coordinate point:
y=7x^2+9x+1
y=-3x+5
(2/7,29/7) and (-2,11)
Solve:
4x^(3/8)-25=7
x=256
Write the equation of the transformed function: 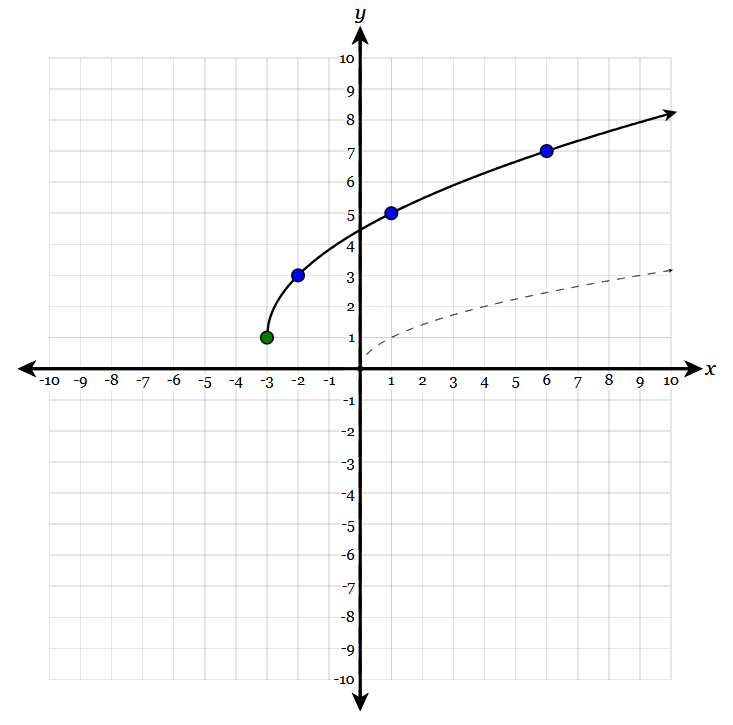
y=2sqrt(x+3)+1