Formulas
Rectangular Prisms
Triangular Prisms
Cylinders
Real-World Applications
100
What is the formula for the surface area of a rectangular prism?
SA = 2(lw + lh + wh)
100
Find the surface area of a box that is 4 cm long, 3 cm wide, and 2 cm high.
SA = 2(4×3 + 4×2 + 3×2) = 52 cm²
100
A triangular prism has triangle bases with base 4 cm and height 3 cm. The prism is 6 cm long. The triangle has sides of 3 cm, 4 cm, and 5 cm. Find the surface area.
Step 1: Area of triangle = ½ × 4 × 3 = 6 cm²
Step 2: 6 × 2 = 12 cm²
Step 3: Rectangle areas = 3×6 = 18, 4×6 = 24, 5×6 = 30 → total = 72 cm²
Step 4: Total SA = 12 + 72 = 84 cm²
100
Find the surface area of a cylinder with radius 3 cm and height 5 cm. Use π ≈ 3.14.
SA = 2π(3²) + 2π(3)(5)
SA = 56.52 + 94.2
SA ≈ 150.72 cm²
100
You want to paint all sides of a small wooden block that’s 3 cm by 4 cm by 5 cm. How much area will you paint?
SA = 2(3×4 + 3×5 + 4×5)
SA = 2(12 + 15 + 20)
SA = 94 cm²
200
What is the formula for the surface area of a triangular prism?
Step 1: calculate area of triangle
Step 2: multiply triangle area by 2 (there are 2 triangles)
Step 3: calculate area of rectangles (there are 3 rectangles, but they may not be the same size, make sure they are identical before multiplying).
Step 4: add the totals together (area of 2 triangles + area of 3 rectangles = total area)
200
A cube has edges of 5 cm. What is its surface area?
SA = 6 × 5² = 150 cm²
200
A triangular prism has triangle bases with base 5 cm and height 4 cm. The triangle’s sides are 5 cm, 3 cm, and 4 cm. The prism is 8 cm long. Find the surface area.
Step 1: Area of triangle = ½ × 5 × 4 = 10 cm²
Step 2: 10 × 2 = 20 cm²
Step 3: Rectangle areas = 5×8 = 40, 3×8 = 24, 4×8 = 32 → total = 96 cm²
Step 4: Total SA = 20 + 96 = 116 cm²
200
A cylinder has radius 4 cm and height 6 cm. What is the surface area?
SA = 2π(16) + 2π(4)(6)
SA ≈ 100.48 + 150.72
SA ≈ 251.2 cm²
200
A chocolate bar is shaped like a triangular prism. The triangular ends are 5 cm² each and the prism is 6 cm long with a triangle perimeter of 10 cm. Find the surface area.
SA = 2(5) + 10×6
SA = 10 + 60
SA = 70 cm²
300
What is the formula for the surface area of a cylinder?
SA = 2πr² + 2πrh
300
A cereal box has dimensions 20ft by 10ft by 5ft. What is the surface area?
SA = 2(20×10 + 20×5 + 10×5) = 700 ft²
300
A prism has triangle bases with base 6 cm and height 5 cm. The triangle has sides 6 cm, 5 cm, and 4 cm. The prism is 10 cm long. Find the surface area.
Step 1: Area of triangle = ½ × 6 × 5 = 15 cm²
Step 2: 15 × 2 = 30 cm²
Step 3: Rectangle areas = 6×10 = 60, 5×10 = 50, 4×10 = 40 → total = 150 cm²
Step 4: Total SA = 30 + 150 = 180 cm²
300
What part of a cylinder is the “lateral surface”?
The curved side that wraps around the cylinder.
300
A can has a label that wraps around its curved surface. If the radius is 3 cm and height is 10 cm, what’s the label area (just the side)?
Lateral area = 2πrh
Lateral area = 2×3.14×3×10
LSA = 188.4 cm²
400
Which part of a 3D object does “lateral surface area” refer to?
The surface area of the sides, not including the bases.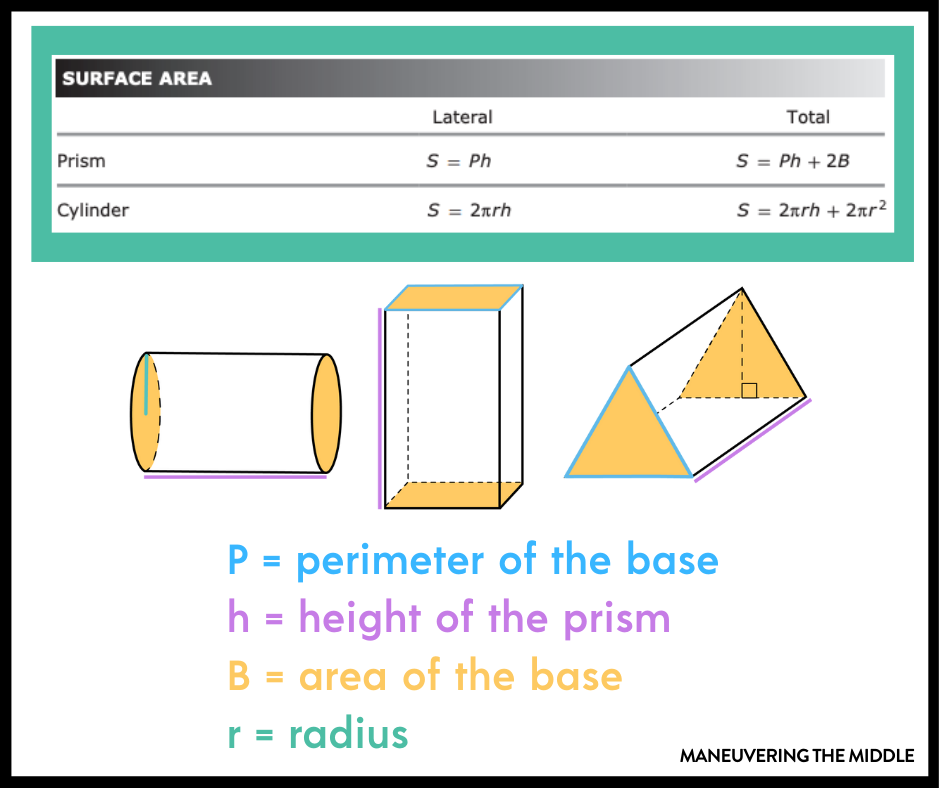
400
If the dimensions of a rectangular prism are 3.22 cm, 4 cm and 7.79cm, what is the surface area?
SA = 2((3.22 x 4) + (4 x 7.79) + (3.22 x7.79))
SA = 2(12.88 + 31.16 + 25.0838)
SA = 2 x 69.1238
SA = 138.25 cm2
400
A triangular prism has triangle bases with base 8 cm and height 6 cm. The triangle’s sides are 8 cm, 6 cm, and 5 cm. The prism is 7 cm long.
Step 1: Area = ½ × 8 × 6 = 24 cm²
Step 2: 24 × 2 = 48 cm²
Step 3: Rectangle areas = 8×7 = 56, 6×7 = 42, 5×7 = 35 → total = 133 cm²
Step 4: Total SA = 48 + 133 = 181 cm²
400
A cylinder has radius 5 cm and height 8 cm. What is the surface area?
SA = 2π(25) + 2π(5)(8)
SA = 157 + 251.2
SA = 408.2 cm² (approx.)
400
A cereal box has dimensions 30 cm by 20 cm by 6 cm. What is its surface area?
SA = 2(30×20 + 30×6 + 20×6)
SA = 2(600 + 180 + 120)
SA = 1800 cm²
500
500: Why do we use 2 in surface area formulas like 2(lw + lh + wh)?
Because each face comes in pairs (top/bottom, front/back, sides).
500
A large crate measures 12 cm by 9 cm by 7 cm. What is its surface area?
SA = 2(12×9 + 12×7 + 9×7)
SA = 2(108 + 84 + 63)
SA = 510 cm²
500
A triangular prism has triangle bases with base 9 cm and height 4 cm. The triangle’s sides are 9 cm, 5 cm, and 6 cm. The prism is 12 cm long.
Step 1: Area = ½ × 9 × 4 = 18 cm²
Step 2: 18 × 2 = 36 cm²
Step 3: Rectangle areas = 9×12 = 108, 5×12 = 60, 6×12 = 72 → total = 240 cm²
Step 4: Total SA = 36 + 240 = 276 cm²
500
500: A cylinder has a radius of 2.5 cm and a height of 10 cm. Find its surface area.
SA = 2π(6.25) + 2π(2.5)(10)
SA = 39.25 + 157.08
SA ≈ 196.33 cm²
500
A tent is shaped like a triangular prism with triangular ends of area 12 m² and perimeter 15 m. It’s 5 m long. What is the surface area?
SA = 2(12) + 15×5
SA = 24 + 75
SA = 99 m²