s = (n-2)*180
s = (n-2)
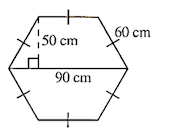
Find the area.


A table top consists of two joined trapezoids as shown in the diagram below. What is the total area of this table top?
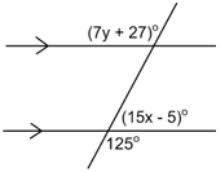
Find the unknown angle measurements.
Top angle = 132 degrees
Right angle = 100
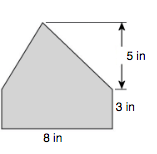
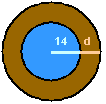
Find the area of the shape.
/_ a,/_ b,/_ c,/_ d
/_ a = 65^@,/_ b = 25^@,/_ c = 25^@,/_ d=75^@
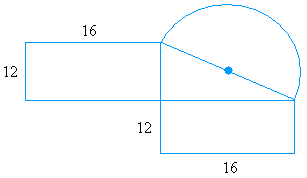
Find the total area.Round to the nearest square unit.
A circular swimming pool with a diameter of 28 feet has a deck of uniform width built around it. If the are aof the deck is 60π square feet, find its width.
Find angles 1 - 9.
/_1 = 90^@
/_2= 152^@
/_3 = 90^@
/_ 4= 98^@
/_ 5= 28^@
/_ 6= 118^@
/_ 7= 128^@
/_ 8= 52^@
/_9 = 62^@
Find the area. Round to the nearest tenth as needed.

/_\ A'BC' ~ /_\ ABC
Find x and y. Found to the nearest tenth.x = 17.1
y = 26.3
A research team wishes to determine the altitude of a mountain as follows: They use a light source at L, mounted on a structure of height 2 meters, to shine a beam of light through the top of a pole P' through the top of the mountain M'. The height of the pole is 20 meters. The distance between the altitude of the mountain and the pole is 1000 meters. The distance between the pole and the laser is 10 meters. Find the altitude h of the mountain. [hint: triangle LP'P ~ triangle LM'M
