(U1)
(U1)
(U2)
(U3)
(U2, U4)
Given the truth table below, evaluate the truth value of: \forall x \exists y F(x,y)
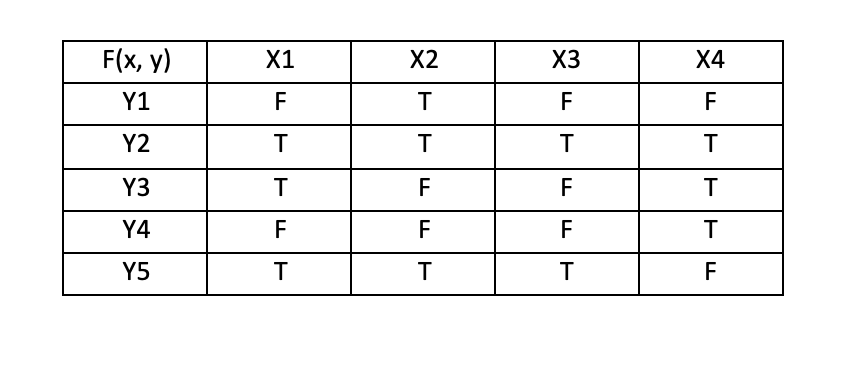
True
Which of the following sets is a family?
(A) { {a, e}, b, c, d}
(B) { a, b, c, d, e }
(C) {{}, {a}, {b}, c }
(D) {{a, b}, {b, c}, {c, a}}
(D) {{a, b}, {b, c}, {c, a}}
A girl scout troop with 10 girls and 2 leaders goes on a hike. When the path narrows they must walk in a single file line with a leader at the front and back of the line. How many ways are there for the entire troop (scouts and leaders) to line up?
2! 10!
Given this postfix expression, determine the original expression (in infix). Note: x and y are variables, * + - ÷ are operators.
3 5 x * + 10 x y ÷ - * y +
(5x+3)(10 - x/y) +y
Sort this set S into equivalence classes mod 7. S = {2, 18, 23, 35, 41, 48, 50, 66, 87, 92}.
[0] = {35}
[1] = {50, 92}
[2] = {2, 23}
[3] = {66, 87}
[4] = {18}
[5] ={}
[6] = {41, 48}
State the converse of: If I study, I will do well on the exam.
Is the converse equivalent to the original statement?
If I do well on the exam, then I studied. No, it is not equivalent.
Is the function f: R \to R , f(x) = -x^3 +4 onto? One-to-one? A bijectiion?
If it is a bijection, find it's inverse.
It is a bijection, and it's inverse is
f^-1(x)= root(3)(4-x).
( (12 + 30 -1), (30-1))
Draw a complete graph on 6 vertices. What is its vertex-connectivity? What is its edge-connectivity?
It is 5-vertex connected and 5-edge connected.

State the logical negation of: Some people use computers, but cannot code.
Everyone either doesn't use a computer, or can code (or both).
Use a truth table to determine if the expression is a tautology, contradiction, or neither: (p \implies q) \iff (p ∧ ¬ q)
Contradiction
Given the graph G, would there be an edge from vertex a to vertex in G^3
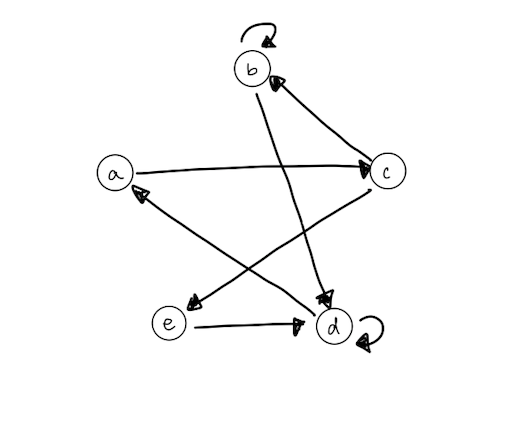
No, there's no path of length three from a to e in G.
There are 20 distinct candies in a bag, and a tutor wants to know the number of ways she could possibly to distribute the candy to her 6 students. All the candies must be given out, but there's no limitation to how many a single student receives. How many ways can she distribute the candy?
6^20
The following parameters are chosen to generate the public and private keys for the RSA cryptosystem.
p = 17 q = 11 e = 131 d = 11
If the ciphertext is c = 5, how would you calculate the plaintext m ?
Bonus: Simplify it to get m!
N = 187, m = cd mod N
m = (5)11 mod 187
= 181 (Bonus!)
Which of the following complete bipartite graphs have a Hamilton Cycle?
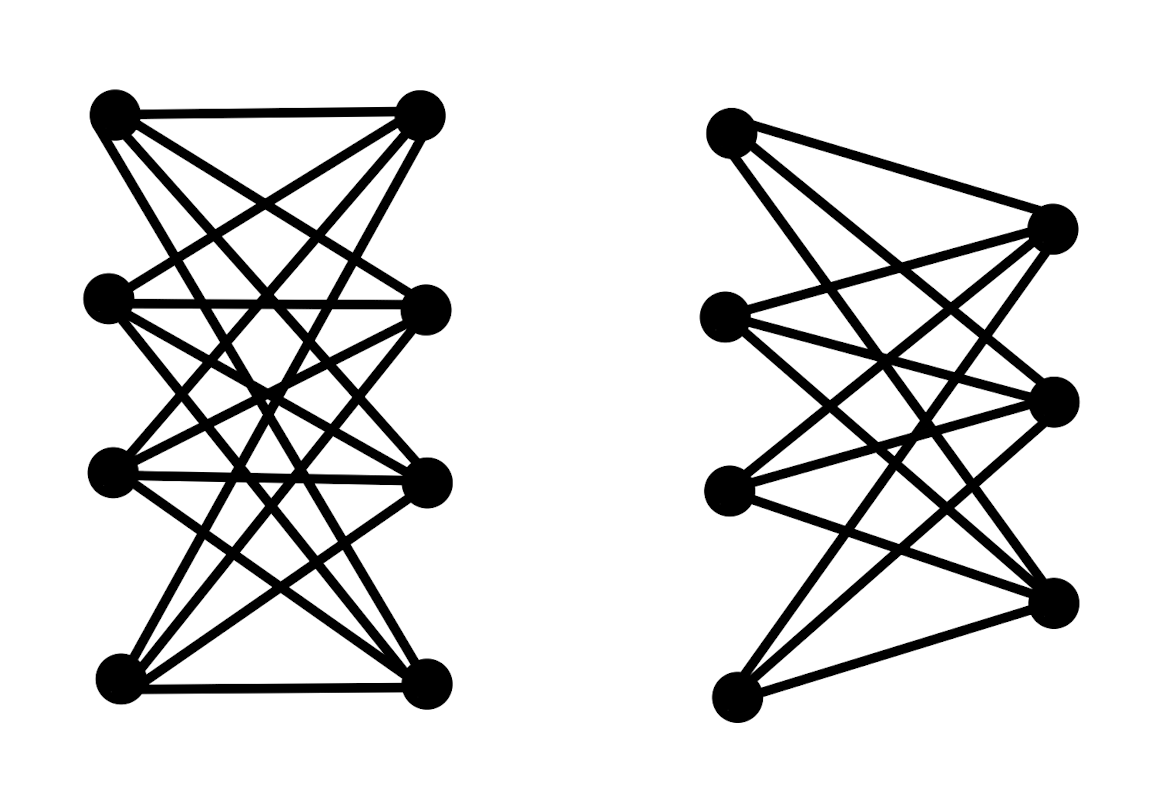
The K4,4 on the right.
Prove that the argument is valid using rules of inference:
j ∨ ¬ s
s ∨ h
\implies j ∨ h
1) j ∨ ¬ s (premise)
2) s ∨ h (premise)
3) ¬ s ∨ j (identity, 2)
4) h ∨ j (resolution)
5) j ∨ h (identity, 4)
Find the algebraic form of the sequence: 110, 60, 10, -40, -90, ... for domain i = 1, 2, 3, ...
a_k = 110 - (k-1)50
In a special lottery game, a player rolls three dice. One is a weighted dice where the probability of rolling a 1 is twice as likely as any other outcome. The player wins if they roll 3 sixes, what is the probability of winning?
(1/6)(1/6)(1/7)
Use Kruskal's Algorithm to find a minimum spanning tree of the following graph.
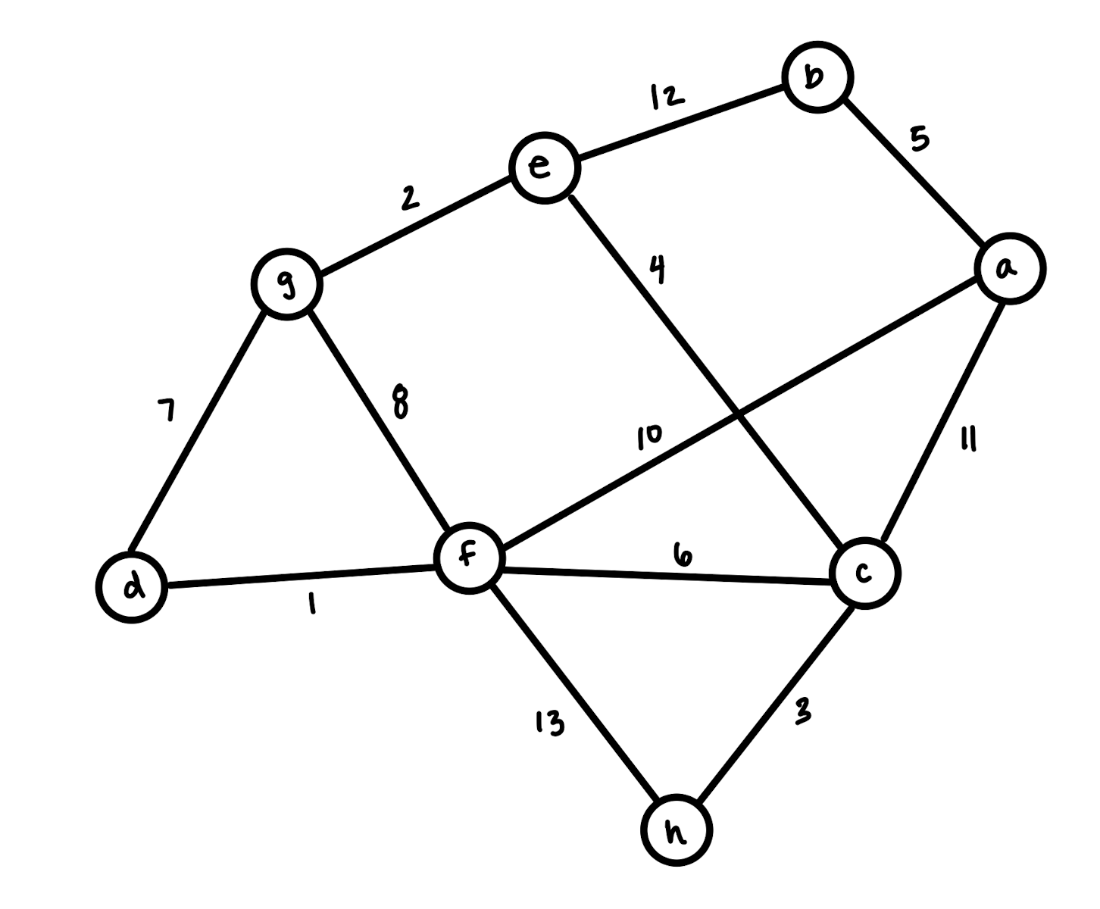 What is the weight of that tree?
What is the weight of that tree?
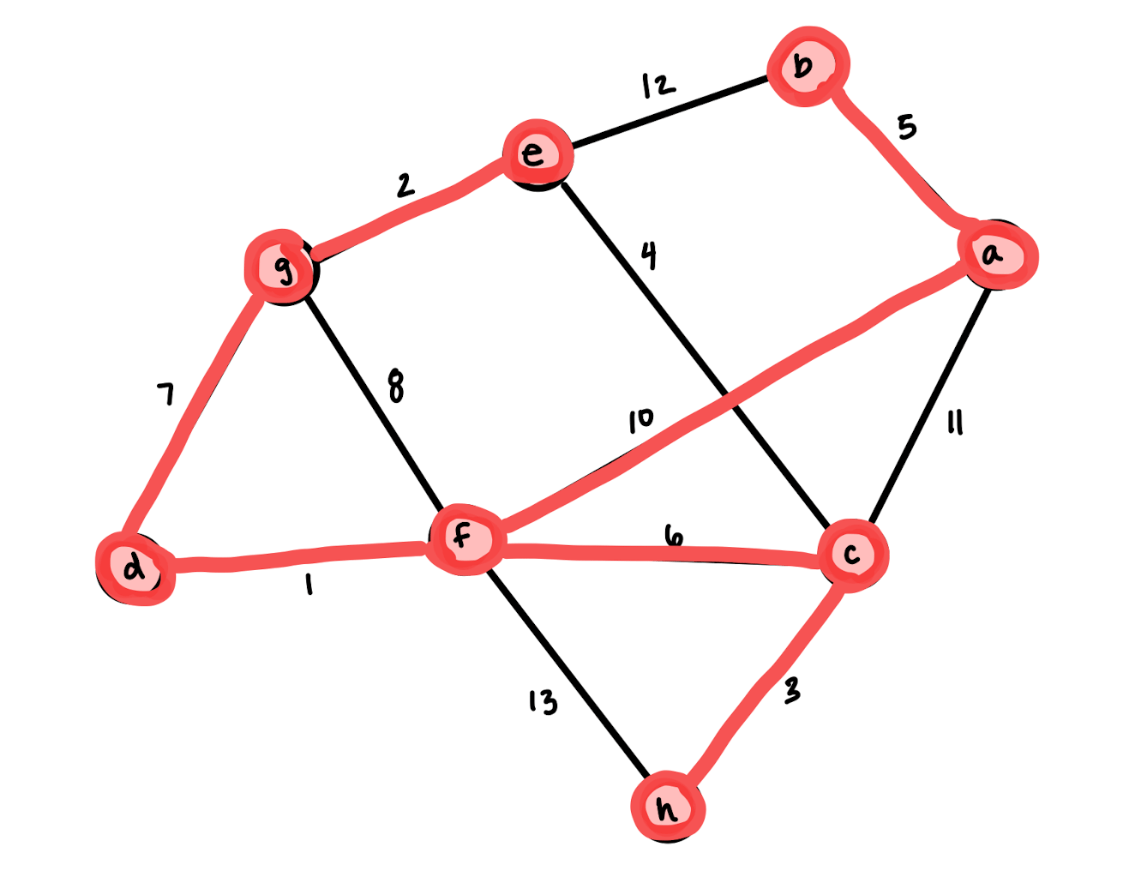
Total weight: 34
Count the number of strings of length 9 over the alphabet {a, b, c} that have exactly two a's, exactly, two b's, or exactly two c's.
|A \cup B \cup C| = |A| +|B|+|C| - |A cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C|
= ((9), (2))2^7 + ((9), (2))2^7 + ((9), (2))2^7 - ((9), (2))((7), (2))- ((9), (2))((7), (2))- ((9), (2))((7), (2)) +0
= 3(((9), (2))2^7) - 3(((9), (2))((7), (2)))
Use contradiction to prove that 2 - sqrt2 is irrational.
Assume that
2- sqrt 2
is rational. Then
2 - sqrt 2 = x/y
, where x and y are integers and y ≠ 0. Add 2 to both sides of the equation to get
2= x/y + sqrt 2
. Subtract
x/y
from both sides of the equation to get
2−x/y= sqrt 2
. The expression
2−x/y
is equal to
(2y−x)/y
. Therefore
sqrt 2=(2y−x)/y
. Since x and y are both integers, 2y-x is also an integer. Furthermore, y is a non-zero integer. Since 2 is equal to the ratio of two integers in which the denominator is non-zero, then we have shown that 2 is rational, contradicting the fact proved earlier that
sqrt 2
is irrational. Therefore the assumption that
2 - sqrt 2
is rational is false and therefore
2 - sqrt 2
must be irrational.
The following matrix represents a relation. Use it to draw a digraph representing the relation and then find the transitive closure of the graph.
[ [1, 1, 0, 1], [0, 1, 0, 0], [1, 1, 0, 0],[0, 1, 0, 1]]
The graph and its transitive closure are the same. 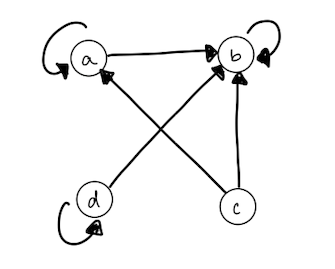
A fair coin is tossed three times. Let Y be the random variable that denotes the square of the number of heads. For example, in the outcome HTH, there are two heads and Y = 4. What is the expected value of Y?
E[Y] = 0·(1/8) + 1·(3/8) + 4·(3/8) + 9·(1/8) = 24/8 = 3.
You're creating an RSA public and private key. You've chosen the primes p = 23 and q = 31, and you've chosen e = 59. What is your private key d?
d is the multiplicative inverse of e mod Phi = (p-1)(q-1)
d = 179
Define the sequence {bn} as follows:
- b0 = 1
- bn = 2bn-1 + 1 for n ≥ 1
Prove using induction that for n ≥ 0, bn = 2n+1 - 1.
By induction on n.
Base case: n=0
b_0 = 2^{0+1} -1 = 1
as defined.
Inductive step: Assume that
b_k = 2^{k+1} -1.
Consider b_{k+1} .
b_{k+1} = 2b_k +1
= 2(2^{k+1}-1) +1
(by the induction hypothesis.)
= 2*2^{k+1} -2 +1
= 2^{k+2} -1.
■